Hi students, Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get Real Numbers CBSE NCERT Notes Class 10 Maths Chapter 1 PDF. You can download this PDF and save it in your mobile device or laptop etc.

Real Numbers CBSE NCERT Notes Class 10 Maths Chapter 1 PDF

Real Numbers

All the rational and the irrational numbers is called real numbers.

For example: -2, 1/3, 0, √2 etc.

Real numbers can be positive or negative.

Euclid Division Lemma

A lemma is a proven statement used for proving another statement.

According to Euclid Division Lemma, for positive integers a and b, there exist unique integers q and r satisfying a = bq + r, where 0 ≤ r < b.

The integers q and r are called the quotient and remainder, respectively. The value of q and r can be zero.

For example:

17 = 6 x 2 + 5,

5 = 12 x 0 + 5,

20 = 4 x 5 + 0 etc.

Euclid Division Algorithm

HCF (Highest Common Factor) of two positive integers a and b is the largest positive integer d that divides both a and b.

It means, if a = dm and b = dn, then d = HCF of a and b.

Euclid’s division algorithm is a method to find the HCF of two given positive integers.

In class 8, you have learnt how to find the HCF of given two numbers by using long division methods. 

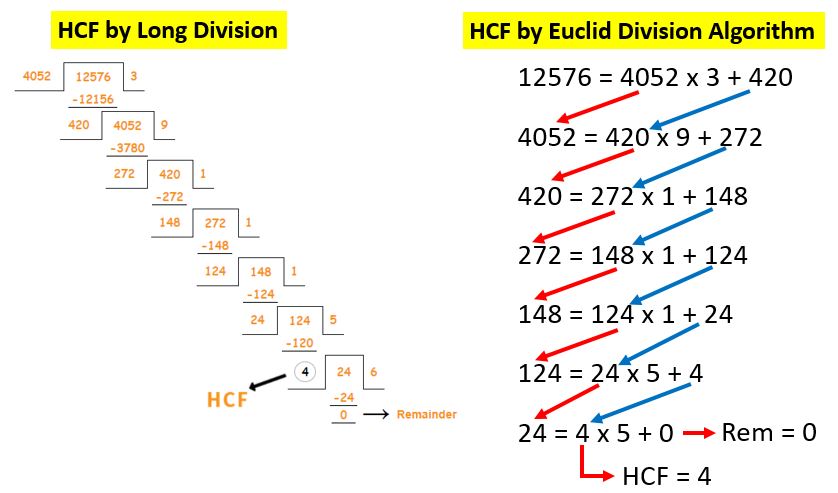
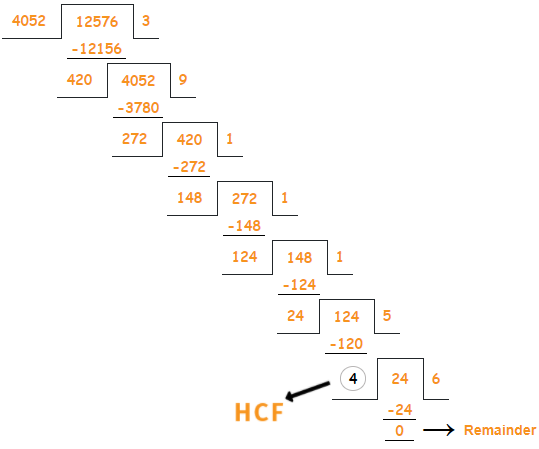
For example: you need to find the HCF of 4052 and 12576 using long division method.

Now, to obtain the HCF of two positive integers, ( let a and b), with a > b, follow the steps below:

Step 1 : Apply Euclid’s division lemma, to a and b. So, you find whole numbers, q and r such that a = bq + r, 0 ≤ r < b.

Step 2 : If r = 0, b is the HCF of a and b. If r ≠ 0, apply the division lemma to b and r.

Step 3 : Continue the process till the remainder is zero. The divisor at this step will be the required HCF.

Class 10 Maths Chapter 1 Examples 1: Find the HCF of 4052 and 12576 using euclid division algorithm (EDA).

Step 1: Since 12576 > 4025, you need to apply EDA to 12576 and 4052. Hence, you will get

12576 = 4052 x 3 + 420.

Step 2: Since the remainder 420 ≠ 0, you need to apply EDA to 4052 and 420. Hence, you will get

4052 = 420 x 9 + 272.

Step 3: Since the remainder 272 ≠ 0, you need to apply EDA to 420 and 272. Hence, you will get

420 = 272 x 1 + 148.

Step 4: Since the remainder 148 ≠ 0, you need to apply EDA to 272 and 148. Hence, you will get

272 = 148 x 1 + 124.

Step 5: Since the remainder 124 ≠ 0, you need to apply EDA to 148 and 124. Hence, you will get

148 = 124 x 1 + 24.

Step 6: Since the remainder 24 ≠ 0, you need to apply EDA to 124 and 24. Hence, you will get

124 = 24 x 5 + 4.

Step 7: Since the remainder 4 ≠ 0, you need to apply EDA to 24 and 4. Hence, you will get

24 = 4 x 6 + 0.

Now, on this step 7, the remainder has become zero, so you need to stops.

Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.

But, you don’t need to write the steps description, you may simply write as below in the solution of copy.

Euclid’s division algorithm is not only useful for calculating the HCF of very large numbers.

In CBSE Class 10 Maths, Euclid’s Division Algorithm is stated for only positive integers. It can be extended for all integers except zero, i.e., b ≠ 0. But, this is not in syllabus of this class.

Euclid’s division lemma/algorithm has many other applications that are related to finding properties of numbers.

Class 10 Maths Chapter 1 Examples 2: Show that every positive even integer is of the form 2q, and that every positive odd integer is of the form 2q + 1, where q is some integer.

According to Euclid division lemma, we have a = bq + r.

If b = 2, then r = 0, 1.

Case 1 : At r = 0, a = 2q is divisible by 2. Thus, 2q is an even integer.

Case 2 : At r = 1, a = (2q + 1) is not divisible by 2. Thus, (2q + 1) is an odd integer.

Therefore, every positive even integer is of the form 2q, and that every positive odd integer is of the form 2q + 1, where q is some integer.

Fundamental Theorem of Arithmetic

Every composite number can be factorized as a product of primes, and this factorization is unique.

According to fundamental theorem of arithmetic, any composite number it can be factorized as a product of prime numbers in a unique way, except for the order in which the primes occur.

Let a composite number x, you factorize it as x = p₁ × p₂ × p₃ × … × p_n, where p₁, p₂, p₃, …, p_n are primes and written in ascending order, i.e., p₁ ≤ p₂ ≤ p₃ ≤ . . . ≤ p_n. If you combine the same primes, you will get powers of primes.

For example: 32760 = 2 × 2 × 2 × 3 × 3 × 5 × 7 × 13 = 2³ × 3² × 5 × 7 × 13.

Class 10 Maths Chapter 1 Examples 3: Find the HCF and LCM of 6, 72 and 120 using prime factorization method.

6 = 2 × 3, 72 = 2³ × 3² , 120 = 2³ × 3 × 5

HCF(6, 72, 120) = Product of the smallest power of each common prime factor in the numbers

HCF(6, 72, 120) = 2¹ × 3¹ = 2 × 3 = 6

LCM(6, 72, 120) = Product of the greatest power of each common prime factor in the numbers

LCM(6, 72, 120) = 2³ × 3² × 5 = 360

Irrational Numbers

An irrational number is a number that cannot be written in the form of p/q, where p and q are integers and q ≠ 0.

An irrational number is also in form of √p, where p is any prime.

For example : √2, √3, √17 etc.

Let p be a prime number. If p divides a², then p divides a, where a is a positive integer.

Class 10 Maths Chapter 1 Examples 4: Prove that √2 is an irrational number.

Let assume that √2 is a rational number.

Then, √2 = p/q, where HCF(p, q) = 1 …(1)

⇒ p = √2q ⇒ p² = 2q² ⇒ 2 divides p².

Then, 2 divides p. Let p = 2m.

Put p = 2m in p² = 2q²

⇒ (2m)² = 2q²

⇒ 4m² = 2q²

⇒ 2m² = q²

⇒ 2 divides q².

Then, 2 divides q. Let p = 2n.

Now, HCF(p, q) = 2 …(2).

In statement (1), we assume that HCF (p, q) = 1 but in statement (2), we get HCF(p, q) = 2.

Thus, we get a contradiction on our assumption, so √2 is NOT a rational number.

Hence, √2 is NOT an irrational number.

Class 10 Maths Chapter 1 Examples 5: Prove that (5 – √3) is an irrational number.

Let assume that (5 – √3) is a rational number.

Then, (5 – √3) = p/q, where HCF(p, q) = 1.

⇒ 5 – p/q = √3

⇒ (5q – p)/q = √3 …(1)

In LHS, (5q – p)/q is a rational as p/q is a rational.

But, in RHS, √3 is an irrational number. 

Thus, the equation (1) is mathematically incorrect.

Therefore, we get a contradiction on our assumption.

Hence, (5 – √3) is NOT a rational number. It is an irrational number.

Terminating and Non-Terminating Decimals

A rational number is also a terminating decimals or a non-terminating and recurring decimals.

An irrational number is also a non-terminating and non-recurring decimals.

Let x = p/q  is a rational number, such that the prime factorization of q(denominator) is of the form 2^m × 5ⁿ, where n, m are non-negative integers. Then x has a decimal expansion which terminates.

If the prime factorization of q(denominator) is NOT in the form of 2^m × 5ⁿ, then x has non-terminating decimals.

Class 10 Maths Chapter 1 Examples 6: Without long division, identify the following as terminating or non-terminating decimals (1) 13/3125 (2) 77/210

(1) 13/3125,

Prime factorization of 3125 = 5⁵ = 2⁰ × 5⁵. Thus, this represents a terminating decimals. 

(1) 77/210,

Prime factorization of 210 = 2 × 3 × 5 × 7. Thus, this represents a non-terminating decimals. 

Click below to get CBSE Class 10 Maths Chapter wise Revision Notes PDF.