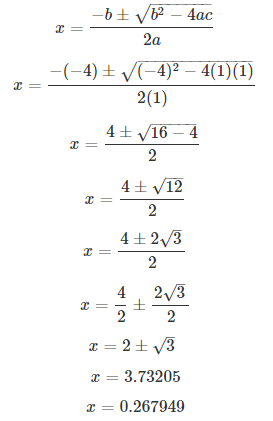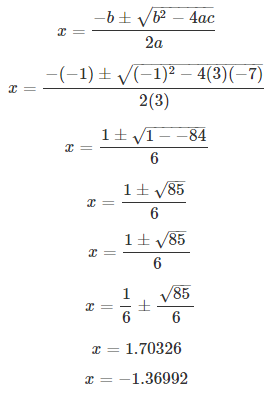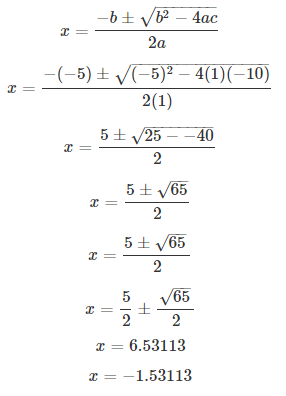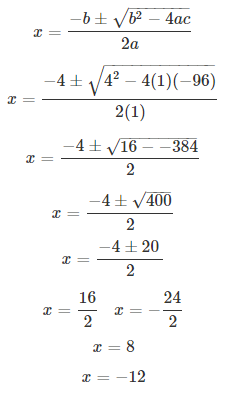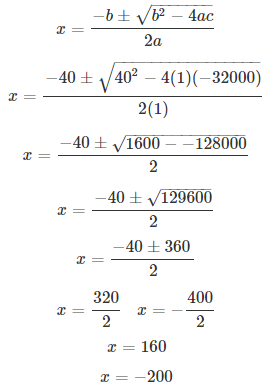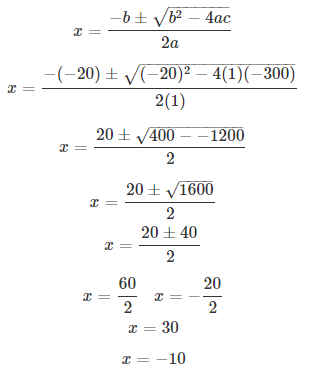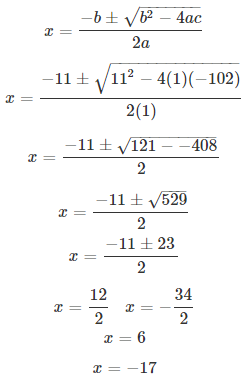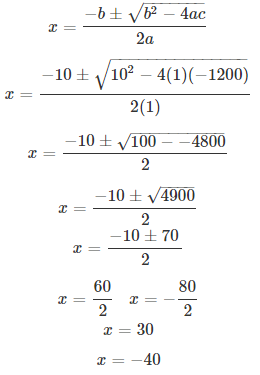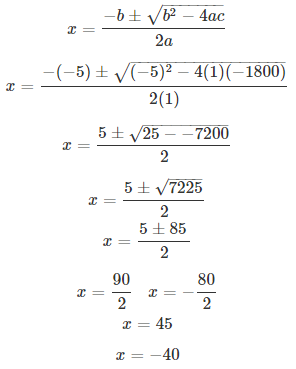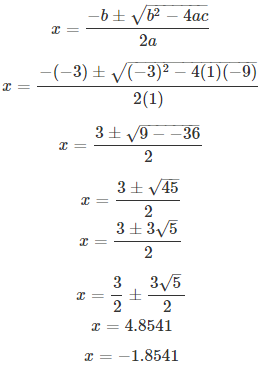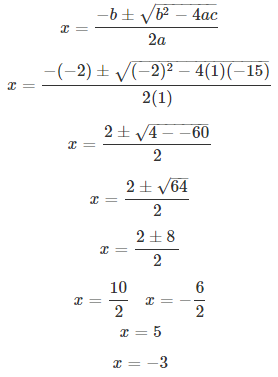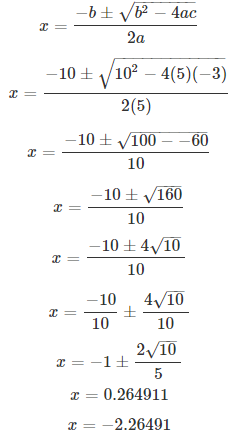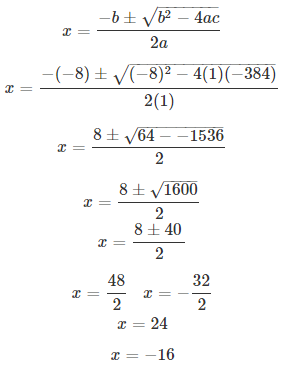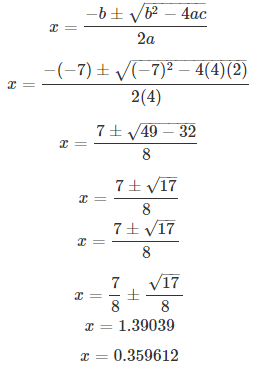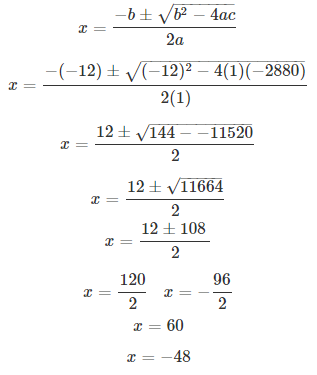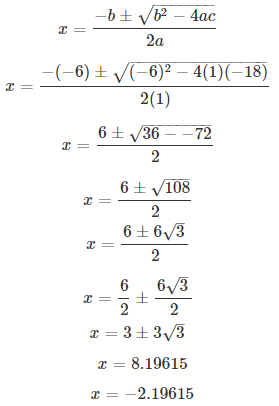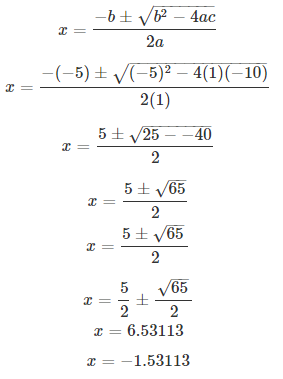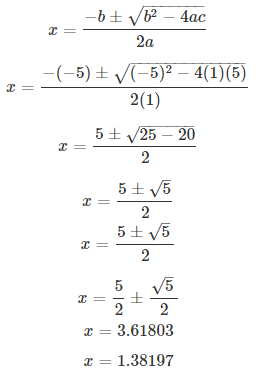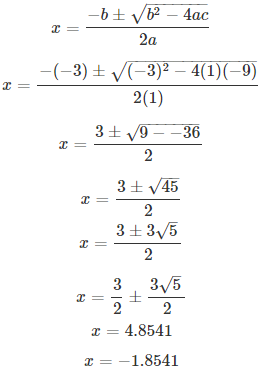S Chand ICSE Maths Solutions Class 10 Chapter 3 Quadratic Equations Revision Exercise
Hi students, Welcome to Amans Maths Blogs (AMB). In this post, you will get S Chand ICSE Maths Solutions Class 10 Chapter 3 Quadratic Equations Revision Exercise. This is the chapter of introduction of ‘Quadratic Equations‘ included in ICSE 2021 Class 10 Maths syllabus.
Read : Quadratic Equations Class 10 ICSE Maths Notes PDF
S Chand ICSE Maths Solutions for Class 10 Chapter 5 Revision Exercise
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 1
Solve for x and give your answer correct to 2 decimal places: x2 – 10x + 6 = 0.
S Chand ICSE Maths Solutions:
Comparing with ax2 + bx + c = 0, we have a = 1, b = -10, c = 6.
On using quadratic formula, we get
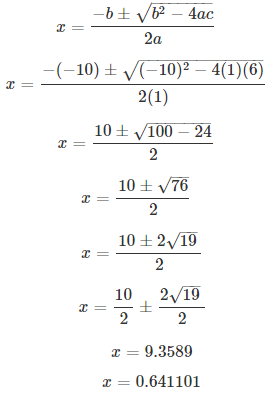
Thus, x = 9.36 or 0.64
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 2
Solve using the quadratic formula : x2 – 4x + 1 = 0.
S Chand ICSE Maths Solutions:
Comparing with ax2 + bx + c = 0, we have a = 1, b = -4, c = 1.
On using quadratic formula, we get
Thus, x = 3.732 or 0.268
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 3
Solve the equation 3x2 – x – 7 = 0 and give your answer correct to two decimal places.
S Chand ICSE Maths Solutions:
Comparing with ax2 + bx + c = 0, we have a = 3, b = -1, c = -7.
On using quadratic formula, we get
Thus, x = 1.70 or -1.37
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 4
Solve the following equation and give your answer up to two decimal places : x2 – 5x – 10 = 0.
S Chand ICSE Maths Solutions:
Comparing with ax2 + bx + c = 0, we have a = 1, b = -5, c = -10.
On using quadratic formula, we get
Thus, x = 6.53 or -1.53
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 5
Solve the equation 2x – 1/x = 7. Write your answer correct to two decimal places.
S Chand ICSE Maths Solutions:
Given that 2x – 1/x = 7 ⇒ 2x2 – 7x – 1 = 0.
Comparing with ax2 + bx + c = 0, we have a = 2, b = -7, c = -1.
On using quadratic formula, we get
Thus, x = 3.64 or -0.14
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 6
The bill for a number of people for overnight stay in Rs. 4800. If there were 4 more, bill each person had to pay would have reduced by Rs. 200. Find the number of people staying overnight.
S Chand ICSE Maths Solutions:
Let the number of people staying overnight is x. Then, bill for each person is Rs. 4800/x.
According to question, we have
4800/(x + 4) = 4800/x – 200
⇒ x2 + 4x – 96 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = 4, c = -96.
On using quadratic formula, we get
Thus, number of people is x = 8.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 7
An aeroplane travelled a distance of 400 km at an average speed of x km/hr. On the return journey, the speed was increased by 40 km/hr. Write down an expression for the time taken by
(i) the onward journey
(ii) the return journey.
If the return journey took 30 minutes less than onward journey, write down an equation in x and find its value.
S Chand ICSE Maths Solutions:
(i) Time taken in onward journey = 400/x hr
(i) Time taken in return journey = 400/(x + 40) hr
Given that 400/(x + 40) – 400/x = 1/2
⇒ x2 + 40x – 32000 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = 40, c = -32000.
On using quadratic formula, we get
Thus, we get x = 160 km/hr
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 8
In an auditorium, seats were arranged in rows and columns. The number of rows were equal to the number of seats in each row. When the number of rows were doubled and the number of seats of seats in each row were reduced by 10, the total number of seats increased by 300. Find
(i) the number of rows in the original arrangement
(ii) the number of seats in the auditorium after rearrangement
S Chand ICSE Maths Solutions:
Let the number of rows is x.
Then, the total number of seats in auditorium is x2.
According to question, 2x(x – 10) = x2 + 300
⇒ x2 – 20x – 300 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -20, c = -300.
Thus, the number of seats in rows in the original arrangement is x = 30
Thus, number of seats in the auditorium after rearrangement is x2 + 300 = 1200
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 9
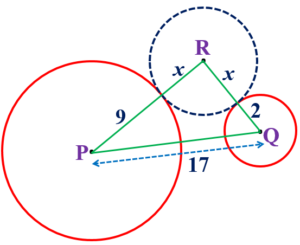
P and Q are centres of circles of radius 9 cm and 2 cm respectively. PQ = 17 cm. R is the centre of a circle of radius x cm, which touches the above circles externally. Given that angle PRQ = 90 degree, write an equation in x and solve it.
S Chand ICSE Maths Solutions:
According to the question, we have
(x + 9)2 + (x + 2)2 = 172
⇒ x2 + 11x – 102 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = 11, c = -102.
Thus, the radius of the circle having center R is x = 6.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 10
By increasing the speed of the car by 10 km/hr, the time of journey for a distance of 72 km is reduced by 36 min. Find the original speed of the car.
S Chand ICSE Maths Solutions:
Let the original speed of the car is x km/hr. Then, time taken for 72 km is 72/x hr.
According to question,
72/(x + 10) = 72/x – 36/60
⇒ x2 + 10x – 1200 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = 1, c = -1200.
Thus, the the original speed of the car is x = 30 km/hr.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 11
A shopkeeper buys a certain number of books for Rs. 720. If the cost per book was Rs. 5 less the number of books that could bought for Rs. 720 would be 2 more. Taking the original cost of each book to be Rs x, write an equation in x and solve it.
S Chand ICSE Maths Solutions:
Given that the original cost of each book to be Rs x. Then, the number of books is 720/x.
According to question,
720/(x – 5) = 720/x + 2
⇒ x2 – 5x – 1800 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -5, c = -1800.
Thus, x = 45.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 12
Solve the quadratic equation for x and give your answer correct to 2 decimal places : x2 – 3x – 9 = 0
S Chand ICSE Maths Solutions:
Comparing with ax2 + bx + c = 0, we have a = 1, b = -3, c = -9.
On using quadratic formula, we get
Thus, x = 4.85 or -1.85
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 13
Five years ago, a women age was the square of her son’s age. Ten years hence her age will be twice that of her son’s age. Find : (i) the age of her son five years ago (ii) the present age of the women.
S Chand ICSE Maths Solutions:
Let, five years ago, son age was x years and his mother’s age was x2 years.
Then, the current age of son is (x + 5) and his mother’s age is (x2 + 5) years.
Now, after 10 years, we have
(x2 + 5 + 10) = 2(x + 5 + 10)
⇒ x2 – 2x – 15 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -2, c = -15.
Thus,
(i) the age of her son five years ago was x = 5 years
(ii) the present age of the women is (x2 + 5) = 30 years.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 14
Solve the following quadratic equation for x and give your answer correct to decimal places 5x(x + 2) = 3.
S Chand ICSE Maths Solutions:
5x(x + 2) = 3
⇒ 5x2 + 10x – 3 = 0
Comparing with ax2 + bx + c = 0, we have a = 5, b = 10, c = -3.
Thus, x = 0.26 or -2.26
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 15
Some students planned a picnic. The budget for the food was Rs 480. As eight of them failed to join the party, the cost of the food for each member increased by Rs 10. Find how many students went for the picnic.
S Chand ICSE Maths Solutions:
Let the number of students went for picnic is x. Then, cost of food for each member is Rs 480/x.
According to question, we have
480/(x – 8) = 480/x + 10
⇒ x2 – 8x – 384 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -8, c = -384.
Thus, required number of students is x = 24.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 16
Solve the following quadratic equation and give the answer correct to two significant figures 4x2 – 7x + 2 = 0.
S Chand ICSE Maths Solutions:
4x2 – 7x + 2 = 0
Comparing with ax2 + bx + c = 0, we have a = 4, b = -7, c = 2.
Thus, x = 1.40 or 0.36
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 17
The speed of an express train is x km/hr and the speed of an ordinary train is 12 km/hr less than that of the express train. If the ordinary train takes one hour longer than the express train to cover a distance of 240 km, find the speed of the express train.
S Chand ICSE Maths Solutions:
Given that the speed of an express train is x km/hr, then the speed of the ordinary train is (x – 12) km/hr.
According to question, we have
⇒ 240/(x – 12) = 240/x + 1
⇒ x2 – 12x – 2880 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -12, c = -2880.
On using quadratic formula, we get
Thus, speed of express train is 60 km/hr.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 18
Without solving the following quadratic equation, find the value of p for which the roots are equal : px2 – 4x + 3 = 0.
S Chand ICSE Maths Solutions:
px2 – 4x + 3 = 0
Comparing with ax2 + bx + c = 0, we have a = p, b = -4, c = 3.
The roots of the equation are equal.
⇒ D = 0
⇒ b2 – 4ac = 0
⇒ (-4)2 – 4(p)(3) = 0
⇒ 16 – 12p = 0
⇒ p = 16/12 = 4/3
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 19
Solve the following equation x – 18/x = 6. Give your answer correct to 2 significant figures.
S Chand ICSE Maths Solutions:
x – 18/x = 6
⇒ x2 – 6x – 18 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -6, c = -18.
On using quadratic formula, we get
Thus, x = 8.20 or -2.20
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 20
Rs 480 is divided equally among x children. If the number of children were 20 more, then each would have got Rs. 12 less. Find x.
S Chand ICSE Maths Solutions:
Each child got Rs (480/x).
According to question, we have
480/(x + 20) = 480/x – 12
⇒ x2 + 20x – 800 = 0
⇒ x2 + 40x – 20x – 800 = 0
⇒ x(x + 40) – 20(x + 40) = 0
⇒ (x – 20)(x + 40) = 0
⇒ x = 20 or -40.
Thus, x = 20
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 21
Without solving the following quadratic equation, find the value of m for which the given equation has real and equal roots : x2 + 2(m – 1)x + (m + 5) = 0.
S Chand ICSE Maths Solutions:
x2 + 2(m – 1)x + (m + 5) = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = 2(m – 1), c = (m + 5).
The roots of the equation are equal.
⇒ D = 0
⇒ b2 – 4ac = 0
⇒ [2(m – 1)]2 – 4(1)(m + 5) = 0
⇒ 4(m – 1)2 – 4(m + 5) = 0
⇒ m2 – 2m + 1 – m – 5 = 0
⇒ m2 – 3m – 4 = 0
⇒ m2 – 4m + m – 4 = 0
⇒ m(m – 4) + 1(m – 4) = 0
⇒ (m + 1)(m – 4) = 0
⇒ m = -1 or 4
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 22
A car covers a distance of 400 km at a certain speed. Had the speed been 12 km/hr more, the time taken for the journey would have been 1 hour 40 minutes less. Find the original speed of the car.
S Chand ICSE Maths Solutions:
Let original speed of the car is x km/hr.
According to question, we have
400/(x + 12) = 400/x – 100/60
⇒ x2 + 12x – 2880 = 0
⇒ x2 + 60x – 48x – 2880 = 0
⇒ x(x + 60) – 48(x + 60) = 0
⇒ (x – 48)(x + 60) = 0
⇒ x = 48 or -60
Thus, the original speed of the car is 48 km/hr.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 23
(i) Solve the following equation and calculate the answer correct to two decimal places : x2 – 5x – 10 = 0.
(ii) without solving the following quadratic equation has real and equal roots : x2 + (p – 3)x + p = 0
S Chand ICSE Maths Solutions:
(i) Given that x2 – 5x – 10 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -5, c = -10.
On using quadratic formula, we get
Thus, we get x = 6.53 or -1.53
(ii) x2 + (p – 3)x + p = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = (p – 3), c = p.
The roots of the equation are real and equal.
⇒ D = 0
⇒ b2 – 4ac = 0
⇒ (p – 3)2 – 4(1)(p) = 0
⇒ p2 – 6p + 9 – 4p = 0
⇒ p2 – 10p + 9 = 0
⇒ p2 – 9p – p + 9 = 0
⇒ p(p – 9) – 1(p – 9) = 0
⇒ (p – 1)(p – 9) = 0
⇒ p = 1 or 9
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 24
A shopkeeper purchases a certain number of books for Rs. 960. If the cost per book was Rs. 8 less, the number of books that could be purchased for Rs 960 would be 4 more. Find the number of books.
S Chand ICSE Maths Solutions:
Let the number of books is x.
According to question, we have
960/(x + 4) = 960/x – 8
⇒ x2 + 4x – 480 = 0
⇒ x2 + 24x – 20x – 480 = 0
⇒ x(x + 24) – 20(x + 24) = 0
⇒ (x – 20)(x + 24) = 0
⇒ x = 20 or -24
Thus, the number of books is x = 20.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 25
Solve for x using the quadratic formula. Write your answer correct to two significant figures (x – 1)2 – 3x + 4 = 0.
S Chand ICSE Maths Solutions:
Given that (x – 1)2 – 3x + 4 = 0
⇒ x2 – 2x + 1 – 3x + 4 = 0
⇒ x2 – 5x + 5 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -5, c = 5.
On using quadratic formula, we get
Thus, we get x = 3.62 or 1.38
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 26
A two digit positive number is such that the product of its digit is 6. If 9 is added to the number, the digits interchange their places. Find the number.
S Chand ICSE Maths Solutions:
Let the unit digit of the number is x, then the tens digit is 6/x.
Thus, the number is 10(6/x) + x.
According to question, we have
10(6/x) + x + 9 = 10x + 6/x
⇒ x2 – x – 6 = 0
⇒ x2 – 3x + 2x – 6 = 0
⇒ x(x – 3) + 2(x – 3) = 0
⇒ (x + 2)(x – 3) = 0
⇒ x = 3 or -2
Thus, the unit digit is x = 3 and the tens digit is 6/x = 2 and hence the number is 23.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 27
Find the value of k for which x = 3 is the solution of the quadratic equation, (k + 2)x2 – kx + 6 = 0. Thus, find the roots of the equation.
S Chand ICSE Maths Solutions:
Since x = 3 is the solution of (k + 2)x2 – kx + 6 = 0.
Put x = 3 in (k + 2)x2 – kx + 6 = 0, we get
9(k + 2) – 3k + 6 = 0
⇒ k = -4
Now, put k = -4 in (k + 2)x2 – kx + 6 = 0.
(-4 + 2)x2 – (-4)x + 6 = 0
⇒ -2x2 + 4x + 6 = 0
⇒ x2 – 2x – 3 = 0
⇒ x2 – 3x + x – 3 = 0
⇒ x(x – 3) + 1(x – 3) = 0
⇒ (x + 1)(x – 3) = 0
⇒ x = -1 or 3
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 28
Sum of two natural numbers is 8 and the difference of their reciprocal is 2/15. Find the numbers.
S Chand ICSE Maths Solutions:
Let first number is x and second number is (8 – x).
According to question, we have
1/x – 1/(8 – x) = 2/15
⇒(8 – x – x) / x(8 – x) = 2/15
⇒ 15(8 – 2x) = 2x(8 – x)
⇒ 120 – 30x = 16x – 2x2
⇒ 2x2 – 46x + 120 = 0
⇒ x2 – 23x + 60 = 0
⇒ x2 – 20x – 3x + 60 = 0
⇒ x(x – 20) – 3(x – 20) = 0
⇒ (x – 3)(x – 20) = 0
⇒ x = 3 or 20 and (8 – x) = 5 or -17
Since both numbers are natural, hence the numbers are 3 and 5.
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 29
Solve the quadratic equation x2 – 3(x + 3) = 0. Give your answer correct to two significant figures.
S Chand ICSE Maths Solutions:
x2 – 3(x + 3) = 0
⇒ x2 – 3x – 9 = 0
Comparing with ax2 + bx + c = 0, we have a = 1, b = -3, c = -9.
On using quadratic formula, we get
Thus, x = 4.85 or -1.85
S Chand ICSE Solutions Class 10 Maths Quadratic Equation Revision Exercise: Ques No 30
A bus covers a distance of 240 km at uniform speed. Due to heavy rain its speed gets reduced by 10 km/h and as such it takes two hours longer to cover the total distance. Assuming the uniform speed to be x km/hr from an equation and solve it to evaluate x.
S Chand ICSE Maths Solutions:
According to question, we have
240/(x – 10) = 240/x + 2
⇒ x2 – 10x – 1200 = 0
⇒ x2 – 40x + 30x – 1200 = 0
⇒ x(x – 40) + 30(x – 40) = 0
⇒ (x + 30)(x – 40) = 0
⇒ x = -30 or 40
Thus, the uniform speed of the bus is x = 40 km/hr.