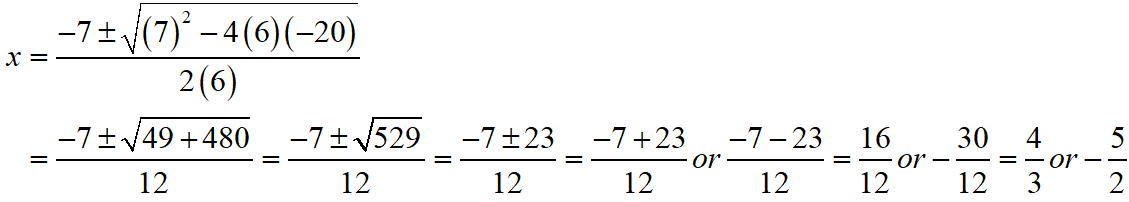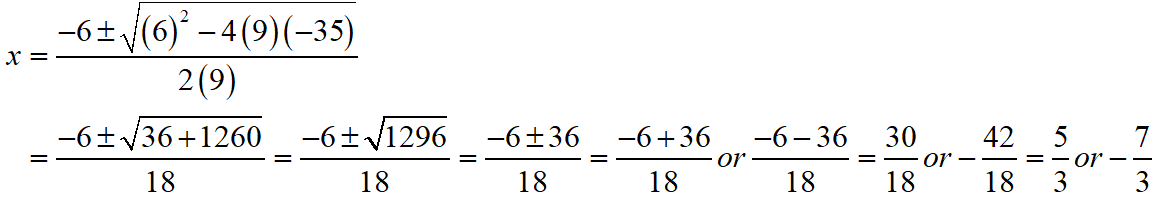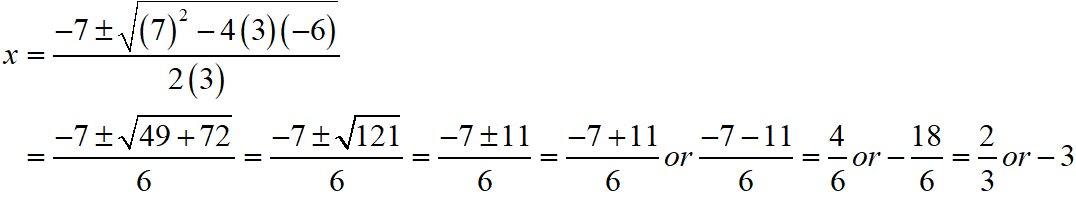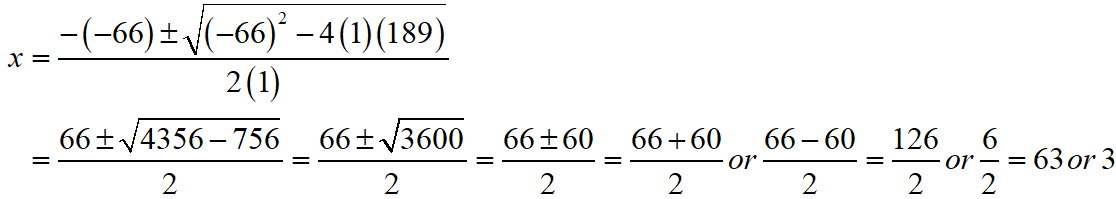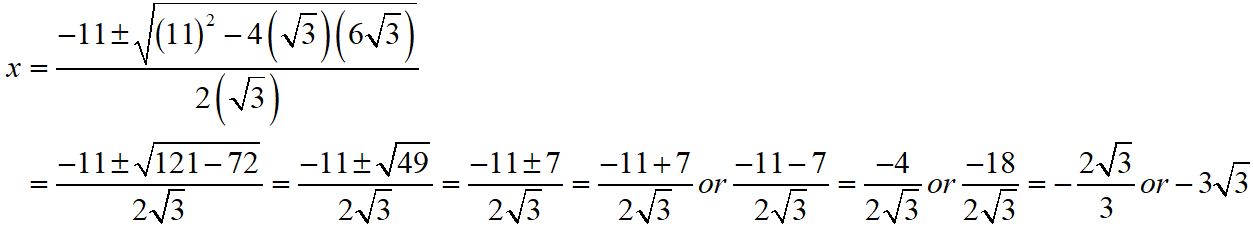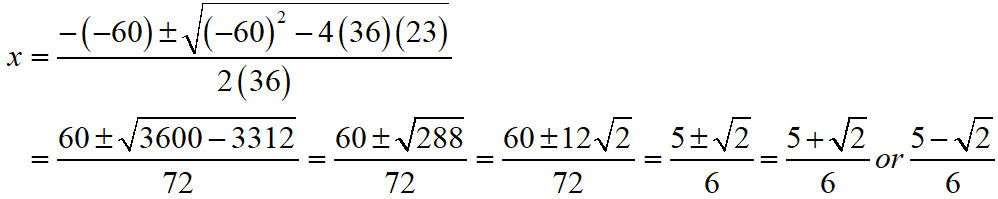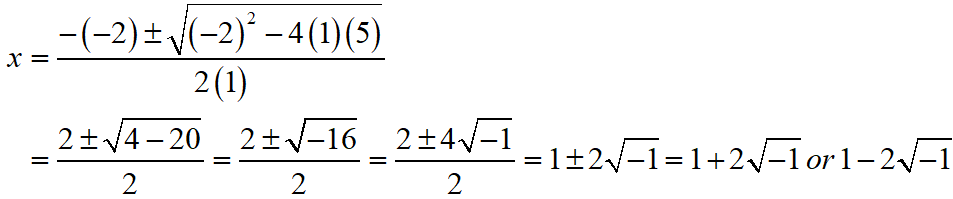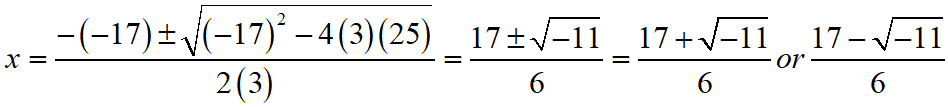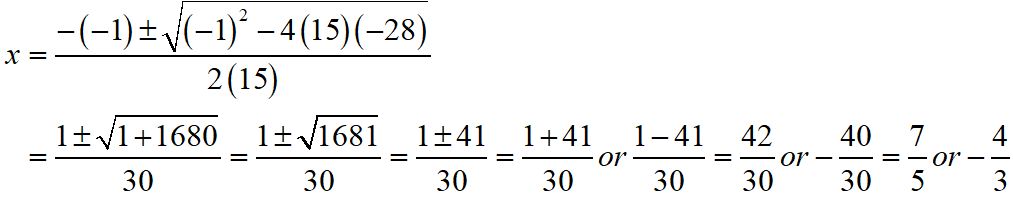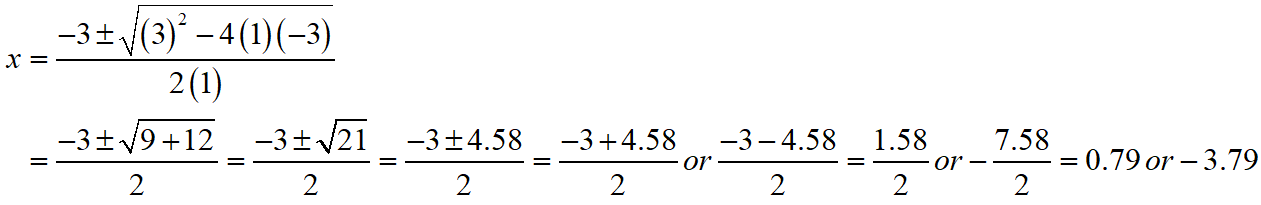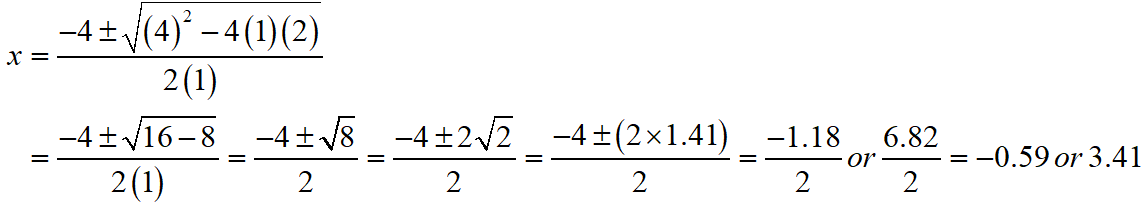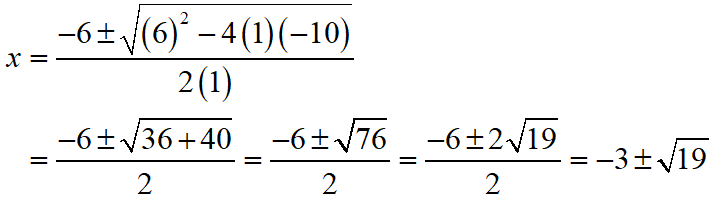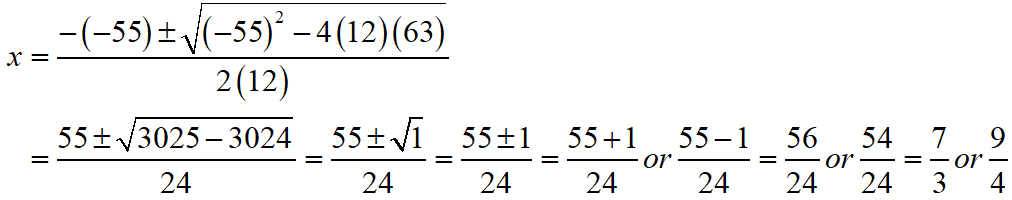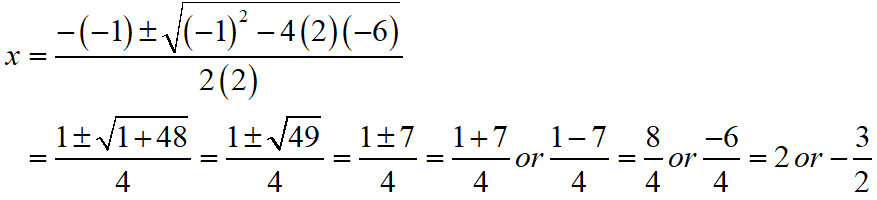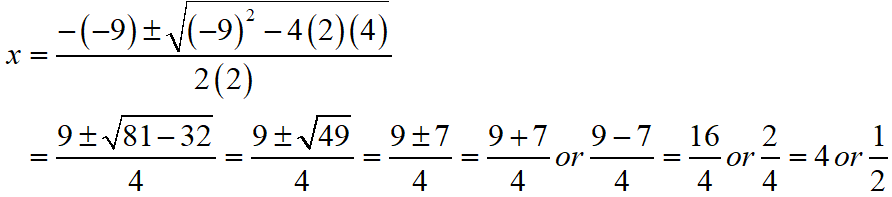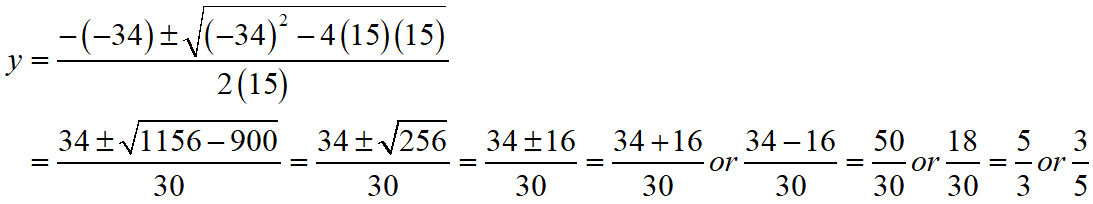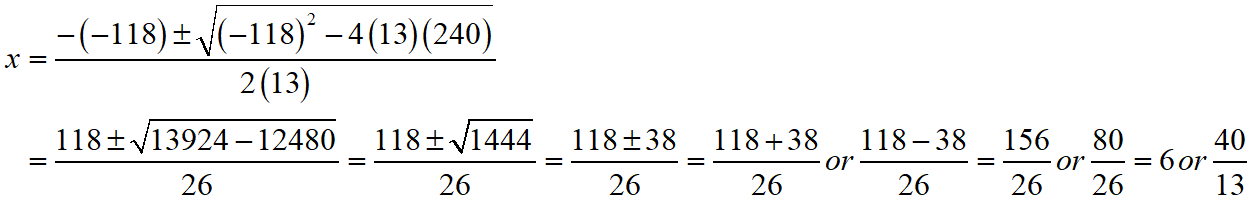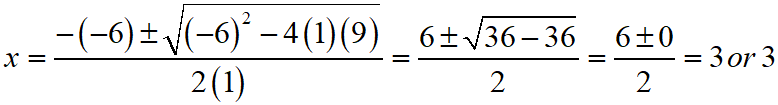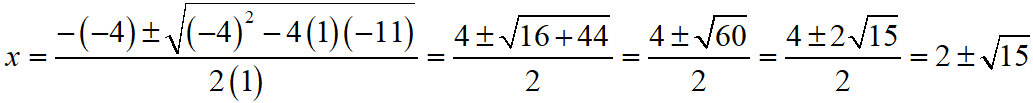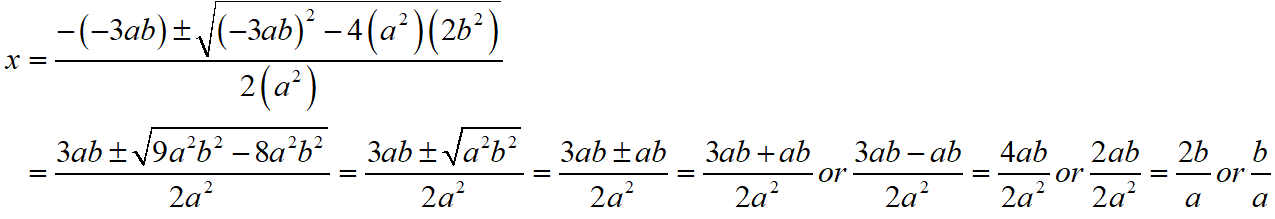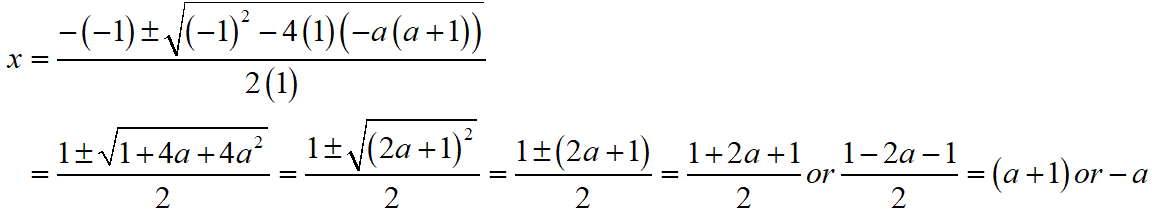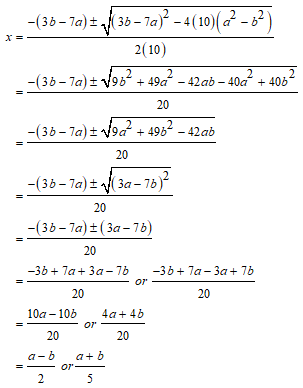S Chand ICSE Maths Solutions Class 10 Chapter 5 Quadratic Equations Exercise 5C

Hi students, Welcome to Amans Maths Blogs (AMB). In this post, you will get S Chand ICSE Maths Solutions Class 10 Chapter 3 Quadratic Equations Exercise 5C. This is the chapter of introduction of ‘Quadratic Equations‘ included in ICSE 2021 Class 10 Maths syllabus.

Read : Quadratic Equations Class 10 ICSE Maths Notes PDF

S Chand ICSE Maths Solutions Class 10 Chapter 5 Quadratic Equations Exercise 5C

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 1

2x² + x – 3 = 0

S Chand ICSE Maths Solutions:

Given that 2x² + x – 3 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 2, b = 1, c = -3

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

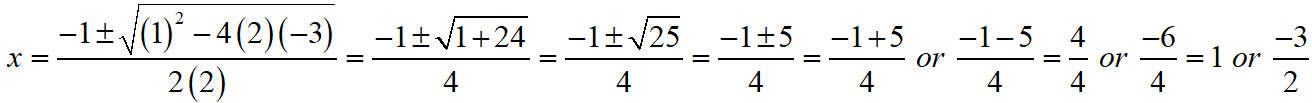
Thus, the roos of the given equation are x = 1 or -3/2.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 2

6x² + 7x – 20 = 0

S Chand ICSE Maths Solutions:

Given that 6x² + 7x – 20 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 6, b = 7, c = -20

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 4/3 or -5/2.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 3

9x² + 6x = 35

S Chand ICSE Maths Solutions:

Given that 9x² + 6x = 35 ⇒ 9x² + 6x – 35 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 9, b = 6, c = -35

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 5/3 or -7/3.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 4

3x² + 7x – 6 = 0

S Chand ICSE Maths Solutions:

Given that 3x² + 7x – 6 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 3, b = 7, c = -6

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 2/3 or -3.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 5

x² – 66x + 189 = 0

S Chand ICSE Maths Solutions:

Given that x² – 66x + 189 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 1, b = -66, c = 189

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 63 or 3.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 6

√3x² + 11x + 6√3 = 0

S Chand ICSE Maths Solutions:

Given that √3x² + 11x + 6√3 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = √3, b = 11, c = 6√3

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = -2√3/3 or -3√3.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 7

36x² + 23 = 60x

S Chand ICSE Maths Solutions:

Given that 36x² + 23 = 60x ⇒ 36x² – 60x + 23 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 36, b = -60, c = 23

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = (5 + √2)/6 or (5 – √2)/6.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 8

x² – 2x + 5 = 0

S Chand ICSE Maths Solutions:

Given that x² – 2x + 5 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 1, b = -2, c = 5

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = (1 + 2√(-1)) or (1 – 2√(-1)).

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 9

3x² – 17x + 25 = 0

S Chand ICSE Maths Solutions:

Given that 3x² – 17x + 25 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 3, b = -17, c = 25

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = (17 + √(-11))/6 or (17 – √(-11))/6.

S Chand ICSE Solutions Class 10 Maths Quadratic Equations Exercise 5C: Ques No 10

15x² – 28 = x

S Chand ICSE Maths Solutions:

Given that 15x² – 28 = x ⇒ 15x² – x – 28 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 15, b = -1, c = -28

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 7/5 or -4/3.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 11

x² + 3x – 3 = 0, giving your answer correct to two decimal places.

S Chand ICSE Maths Solutions:

Given that x² + 3x – 3 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 1, b = 3, c = -3

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 0.79 or -3.79.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 12

(2/3)x = (-1/6)x² – 1/3, giving your answer correct to two decimal places.

S Chand ICSE Maths Solutions:

Given that (2/3)x = (-1/6)x² – 1/3 ⇒ x² + 4x + 2 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 1, b = 4, c = 2

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 3.41 or -0.59.

S Chand ICSE Maths Solutions Class 10 Quadratic Equations Exercise 5C: Ques No 13

x² + 6x – 10 = 0

S Chand ICSE Maths Solutions:

Given that x² + 6x – 10 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 1, b = 6, c = -10

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = -3-√19 or -3+√19.

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 14

(x² + 8)/11 = 5x – x² – 5

S Chand ICSE Maths Solutions:

Given that (x² + 8)/11 = 5x – x² – 5 ⇒ 12x² – 55x + 63 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 12, b = -55, c = 63

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 7/3 or 9/4.

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 15

y – 3/y = 1/2

S Chand ICSE Maths Solutions:

Given that y – 3/y = 1/2 ⇒ 2y² – y – 6 = 0.

Then, comparing this quadratic equation with ay² + by + c = 0, we get a = 2, b = -1, c = -6

Putting the values of a, b and c quadratic formula y = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are y = 2 or -3/2.

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 16

2x + 4/x = 9

S Chand ICSE Maths Solutions:

Given that 2x + 4/x = 9 ⇒ 2x² – 9x + 4 = 0.

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 2, b = -9, c = 4

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 4 or 1/2.

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 17

x/(x + 1) + (x + 1)/x = 34/15, x ≠ 0, x ≠ -1.

S Chand ICSE Maths Solutions:

Given that x/(x + 1) + (x + 1)/x = 34/15

Put y = x/(x + 1), then

⇒ y + 1/y = 34/15

⇒ 15y² – 34y + 15 = 0

Then, comparing this quadratic equation with ay² + by + c = 0, we get a = 15, b = -34, c = 15

Putting the values of a, b and c quadratic formula y = [- b ± √(b² – 4ac)]/2a.

If y = 5/3, then

x/(x + 1) = 5/3

⇒ 3x = 5x + 5

⇒ 2x = -5

⇒ x = -5/2

If y = 3/5, then

x/(x + 1) = 3/5

⇒ 5x = 3x + 3

⇒ 2x = 3

⇒ x = 3/2

Thus, the roos of the given equation are x = -5/2 or 3/2

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 18

2x/(x – 4) + (2x – 5)/(x – 3) = 8 1/3

S Chand ICSE Maths Solutions:

Given that 2x/(x – 4) + (2x – 5)/(x – 3) = 8 1/3 

⇒ [2x(x – 3) + (2x – 5)(x – 4)]/(x – 4)(x – 3) = 25/3

⇒ 3[2x² – 6x + 2x² – 13x + 20] = 25(x – 4)(x – 3)

⇒ 3[4x² – 19x + 20] = 25(x² – 7x + 12)

⇒ 12x² – 57x + 60 = 25x² – 175x + 300

⇒ 13x² – 118x + 240 = 0

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 13, b = -118, c = 240

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 6 or 40/13.

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 19

(x + 6)/(x + 7) – (x + 1)/(x + 2) = 1/(3x + 1)

S Chand ICSE Maths Solutions:

Given that (x + 6)/(x + 7) – (x + 1)/(x + 2) = 1/(3x + 1) 

⇒ [(x + 6)(x + 2) – (x + 1)(x + 7)]/(x + 7)(x + 2) = 1/(3x + 1)

⇒ (3x + 1)(x² + 8x + 12 – x² – 8x – 7) = (x² + 9x + 14)

⇒ 5(3x + 1) = (x² + 9x + 14)

⇒ 15x + 5 = x² + 9x + 14

⇒ x² – 6x + 9 = 0 

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 1, b = -6, c = 9

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 3 or 3.

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 20

(x + 1)/(2x + 5) = (x + 3)/(3x + 4)

S Chand ICSE Maths Solutions:

Given that (x + 1)/(2x + 5) = (x + 3)/(3x + 4)

⇒ (x + 1)(3x + 4) = (x + 3)(2x + 5)

⇒ 3x² + 7x + 4 = 2x² + 11x + 15

⇒ x² – 4x – 11 = 0

Then, comparing this quadratic equation with ax² + bx + c = 0, we get a = 1, b = -4, c = -11

Putting the values of a, b and c quadratic formula x = [- b ± √(b² – 4ac)]/2a.

Thus, the roos of the given equation are x = 2 + √15 or 2 – √15.

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 21(i)

Solve using quadratic formula : a²x² – 3abx + 2b² = 0

S Chand ICSE Maths Solutions:

Given that a²x² – 3abx + 2b² = 0

Then, comparing this quadratic equation with Ax² + Bx + C = 0, we get A = a², B = -3ab, C = 2b²

Putting the values of A, B and C quadratic formula x = [- B ± √(B² – 4AC)]/2A.

Thus, the roos of the given equation are x = 2b/a or b/a.

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 21(ii)

Solve using quadratic formula : x² – x – a(a + 1) = 0

S Chand ICSE Maths Solutions:

Given that x² – x – a(a + 1) = 0

Then, comparing this quadratic equation with Ax² + Bx + C = 0, we get A = 1, B = -1, C = -a(a + 1)

Putting the values of A, B and C quadratic formula x = [- B ± √(B² – 4AC)]/2A.

Thus, the roos of the given equation are x = -a or (a + 1).

S Chand ICSE Solutions Class 10 Math Quadratic Equations Exercise 5C: Ques No 21(iii)

Solve using quadratic formula : 10x² + 3bx + a² – 7ax – b² = 0

S Chand ICSE Maths Solutions:

Given that 10x² + 3bx + a² – 7ax – b² = 0

⇒ 10x² + (3b – 7a)x + (a² – b²) = 0

Then, comparing this quadratic equation with Ax² + Bx + C = 0, we get A = 10, B = (3b – 7a), C = (a² – b²).

Putting the values of A, B and C quadratic formula x = [- B ± √(B² – 4AC)]/2A.

Thus, the roos of the given equation are x = (a – b)/2 or (a + b)/5.

icse 2021icse boardicse class 10 maths chapter 5 solutionsicse class 10 maths chapter wise important questionsicse class 10 maths s chand solutionsicse class 10 maths solutionsicse solutionsicse solutions class 10icse solutions class 10 previous year question papersicse solutions class 10 s chandicse solutions class 10 textbook pdficse solutions for class 10icse solutions for class 10 mathsicse syllabusquadratic equationquadratic equation class 10quadratic equation class 10 extra questionsquadratic equation class 10 icsequadratic equation class 10 icse board questionsquadratic equation class 10 icse important questionsquadratic equation class 10 icse notesquadratic equation class 10 icse s chandquadratic equation class 10 icse solutionsquadratic equation formulaquadratic equation questionsquadratic equation solution class 10 icse ml aggarwal