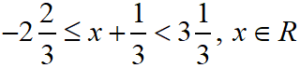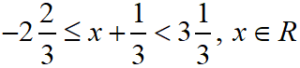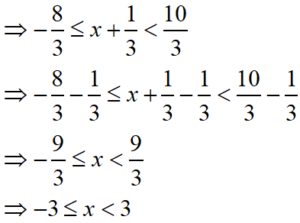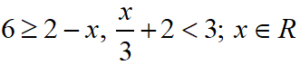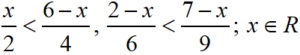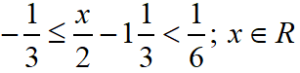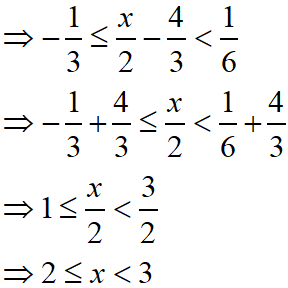S Chand ICSE Maths Solutions for Class 10 Chapter 4 Linear Inequations in One Variables
Hi students, Welcome to Amans Maths Blogs (AMB). In this post, you will get S Chand ICSE Maths Solutions for Class 10 Chapter 4 Linear Inequations in One Variable Exercise 4. This is the fourth chapter ‘Linear Inequations in One Variables‘ included in ICSE 2021 Class 10 Maths syllabus.
Read : Linear Inequalities Class 10 ICSE Maths Notes PDF
S Chand ICSE Maths Solutions for Class 10 Chapter 4 Exercise 4
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 1
On a bargain counter, the shopkeeper puts labels on various goods showing their prices, Rs. P, where P is real numbers. Write a mathematical sentences for each of the following labels
(a) more than Rs. 7.50
(b) not less than Rs. 10
(c) not more than Rs. 22
(d) less than Rs. 11
S Chand ICSE Maths Solutions:
Since the price on label is Rs P, then
(a) more than Rs. 7.50 ⇒ P > 7.50
(b) not less than Rs. 10 ⇒ P ≮ 10 or P ≥ 10
(c) not more than Rs. 22 ⇒ P ≯ 22 or P ≤ 10
(d) less than Rs. 11 ⇒ P < 11
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 2
You are given the following numbers : -2.6, 5.1, -3, 0.4, 1.2, -3.1, 4.7
Fill in the blanks
(a) A = {x : x ≥ -3 } = {……..}
(b) B = {x : x ≤ 1 } = {……..}
S Chand ICSE Maths Solutions:
You are given the following numbers : -2.6, 5.1, -3, 0.4, 1.2, -3.1, 4.7
It mean, you are given a replacement set as U = {-3.1, -3, -2.6, 0.4, 1.2, 4.7, 5.1}.
(a) Solution of A = {x : x ≥ -3 } = {-3, -2.6, 0.4, 1.2, 4.7, 5.1}
(b) Solution of B = {x : x ≤ 1 } = {-3.1, -3, -2.6, 0.4}
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 3
If the replacement set is {-2, -1, +1, +2, +4, +5, +9}, what is the solution set of each of the following mathematical senetences.
(a) x + 3/2 > 5/2
(b) x – 4 = -3
(c) 2x – 5 ≥ 10
(d) 3y/2 ≤ 5/2
(e) 4x2 = 16.
S Chand ICSE Maths Solutions:
Since the replacement set is {-2, -1, +1, +2, +4, +5, +9}, then
(a) Solution set of x + 3/2 > 5/2 ⇒ x > 5/2 – 3/2 ⇒ x > 1 is {+2, +4, +5, +9}.
(b) Solution set of x – 4 = -3 ⇒ x = -3 + 4 ⇒ x = 1 is {+1}.
(c) Solution set of 2x – 5 ≥ 10 ⇒ 2x ≥ 15 ⇒ x ≥ 7.5 is {+9}.
(d) Solution set of 3y/2 ≤ 5/2 ⇒ 3y ≤ 5 ⇒ y ≤ 5/3 ⇒ y ≤ 1.66 is {-2, -1, +1}.
(e) Solution set of 4x2 = 16 ⇒ x2 = 4 ⇒ x = +2 or -2 is {-2, +2}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 4
List the solution set of 30 – 4(2x – 1) < 30, given that x is a positive integer.
S Chand ICSE Maths Solutions:
Since the replacement set is a positive integer, then
Solution set of
30 – 4(2x – 1) < 30
⇒ -4(2x – 1) < 30 – 30
⇒ -4(2x – 1) < 0
⇒ (2x – 1) > 0
⇒ x > 1/2
⇒ x > 0.5
is x = {1, 2, 3, 4, 5,…}
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 5
If the replacement set is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, what is the solution set of each of the following mathematical senetences.
(a) x + 4/3 = 7/3
(b) 2x + 1 < 3
(c) x – 6 > 10 – 6
(d) x + 5 = 20
(e) 2x + 3 ≥ 17
S Chand ICSE Maths Solutions:
Since the replacement set is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, then
(a) Solution set of x + 4/3 = 7/3 ⇒ x = 3/3 ⇒ x = 1 is {1}.
(b) Solution set of 2x + 1 < 3 ⇒ 2x < 2 ⇒ x < 1 is {0}.
(c) Solution set of x – 6 > 10 – 6 ⇒ x > 10 is φ.
(d) Solution set of x + 5 = 20 ⇒ x = 15 is φ.
(e) Solution set of 2x + 3 ≥ 17 ⇒ 2x ≥ 14 ⇒ x ≥ 7 is {7, 8, 9}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 6
(a) x ∈ {2, 4, 6, 9} and y ∈ {4, 6, 18, 27, 54}. Form all ordered pairs (x, y) such that x is a factor of y and x < y.
(b) Find the truth set of the inequality x > y + 2, where (x, y) ∈ {(1, 2), (2, 3), (5, 1), (7, 3), (5, 6)}
S Chand ICSE Maths Solutions:
(a) x ∈ {2, 4, 6, 9} and y ∈ {4, 6, 18, 27, 54}.
(x, y) = x is a factor of y and x < y.
2 is a factor of 4, 6, 18, 54 and 2 < 4, 2 < 6, 2 < 18, 2 < 54, then (x, y) forms the ordered pairs as (2, 4), (2, 6), (2, 18), (2, 54).
4 is a factor of 4 but 4 = 4, then (4, 4) is not in (x, y).
6 is a factor of 18, 54 and 6 < 18, 6 < 54, then (x, y) forms the ordered pairs as (6, 18), (6, 54).
9 is a factor of 18, 27, 54 and 9 < 18, 9 < 27, 9 < 54 then (x, y) forms the ordered pairs as (9, 18), (9, 27), (9, 54).
Thus, the solution set of (x, y) is {(2, 4), (2, 6), (2, 18), (2, 54), (6, 18), (6, 54), (9, 18), (9, 27), (9, 54)}.
(b) Given inequality is x > y + 2. It means x is greater than y + 2.
In {(1, 2), (2, 3), (5, 1), (7, 3), (5, 6)}, we see that (5, 1) and (7, 3) are two pairs which satisfy the given inequality.
Thus, the solution set of (x, y) is {(5, 1), (7, 3)}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 7
Find out the truth set of the following open sentences replacement sets are given
(i) 5/x > 7 ; {1, 2}
(ii) 5/x > 2 ; {1, 2, 3, 4, 5, 6}
(iii) x2 = 9 ; {-3, -2, -1, 1, 2, 3}
(iv) x + 1/x = 2 ; {0, 1, 2, 3}
(v) 3x2 < 2x ; {-4, -3, -2, -1, 0, 1, 2, 3, 4}
(vi) 2(x – 3) < 1 ; {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
S Chand ICSE Maths Solutions:
(i) Given replacement set is {1, 2}.
Now given inequality is 5/x > 7 ⇒ x < 5/7 ⇒ x < 0.71
Thus, the solution set of the given inequality is x ∈ φ.
(ii) Given replacement set is {1, 2, 3, 4, 5, 6}.
Now given inequality is 5/x > 2 ⇒ x < 5/2 ⇒ x < 2.5
Thus, the solution set of the given inequality is x ∈ {1, 2}.
(iii) Given replacement set is {-3, -2, -1, 1, 2, 3}.
Now given equation is x2 = 9 ⇒ x = 3 or -3.
Thus, the solution set of the given equation is x ∈ {-3, 3}.
(iv) Given replacement set is {0, 1, 2, 3}.
Now given equation is x + 1/x = 2 ⇒ (x2 + 1) = 2x ⇒ (x2 -2x + 1) = 0 ⇒ (x – 1)2 = 0 ⇒ (x – 1) = 0 ⇒ x = 1.
Thus, the solution set of the given equation is x ∈ {1}.
(v) Given replacement set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}.
Now given inequality is 3x2 < 2x ⇒ 3x2 – 2x < 0 ⇒ x(3x – 2) < 0 ⇒ 0 < x < 2/3 ⇒ 0 < x < 0.66
Thus, the solution set of the given inequality is x ∈ φ.
(vi) Given replacement set is {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Now given inequality is 2(x – 3) < 1 ⇒ x – 3 < 0.5 ⇒ x < 3.5.
Thus, the solution set of the given inequality is x ∈ {1, 2, 3}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 8
Statement: The sum of the lengths of any two sides of a triangle is always greater than the length of its third side.
Let x, x+1, x+2 be the lengths of the three sides of a triangle.
(i) Write down the three inequations in x, each of which represents the given statement.
(ii) List the set of possible values of x which satisfy all the three inequations obtained in your answer to part (i) above, given that x is an integer.
S Chand ICSE Maths Solutions:
The lengths of the three sides of a triangle are x, x+1, x+2.
(i)
Since the sum of the lengths of any two sides of a triangle is always greater than the length of its third side, we have three inequality as below.
x + (x + 1) > (x + 2) ⇒ 2x + 1 > x + 2 ⇒ x > 1 …(1)
x + (x + 2) > (x + 1) ⇒ 2x + 2 > x + 1 ⇒ x > -1 …(2)
(x + 1) + (x + 2) > x ⇒ 2x + 3 > x ⇒ x > -3 …(3)
On combining (1), (2), (3), we get x > 1.
(ii) Since replacement set of x is an integer, means x ∈ {…, -3, -2, -1, 0, 1, 2, 3, …}.
The solution set of x > 1 is x ∈ { 2, 3, 4, …}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 9
Answer True or False
(a) If x + 10 = y + 14, then x > y
(b) |-4| – 4 = 8
(c) If 10 – x > 3, then x < 7
(d) If p = q + 2, then p > q
(e) If a and b are two negative integers such that a < b, then 1/a < 1/b
(f) 3 ∈ {x : 3x – 2 ≥ 5}
S Chand ICSE Maths Solutions:
(a) x + 10 = y + 14 ⇒ x – y = 14 – 10 ⇒ x – y = 4 ⇒ x – y > 0 ⇒ x > y.
Thus, the given statement “If x + 10 = y + 14, then x > y” is TRUE.
(b) |-4| – 4 = 4 – 4 = 0
Thus, the given statement “|-4| – 4 = 8” is FALSE.
(c) 10 – x > 3 ⇒ 10 – 3 > x ⇒ 7 > x ⇒ x > 7
Thus, the given statement “If 10 – x > 3, then x < 7” is TRUE.
(d) p = q + 2 ⇒ p – q = 2 ⇒ p – q > 0 ⇒ p > q
Thus, the given statement “If p = q + 2, then p > q” is TRUE.
(e) a < b ⇒ 1/a > 1/b
Thus, the given statement “If a and b are two negative integers such that a < b, then 1/a < 1/b” is FALSE.
(f) 3x – 2 ≥ 5 ⇒ 3x ≥ 7 ⇒ x ≥ 7/3 ⇒ x ≥ 2.3
Thus, the given statement “3 ∈ {x : 3x – 2 ≥ 5}” is TRUE.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 10
Find the solution of the inequation 2 ≤ 2p – 3 ≤ 5. Hence graph the solution set on the number line.
S Chand ICSE Maths Solutions:
2 ≤ 2p – 3 ≤ 5 ⇒ 5 ≤ 2p ≤ 8 ⇒ 5/2 ≤ p ≤ 4 ⇒ 2.5 ≤ p ≤ 4
The solution on the number line is as below.

S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 11
If x is a negative integer, find the solution set of 2/3 + (x + 1)/3 > 0.
S Chand ICSE Maths Solutions:
2/3 + (x + 1)/3 > 0 ⇒ (x + 1)/3 > -2/3 ⇒ x + 1 > -2 ⇒ x > -3 …(1)
Since the replacement set of x is negative integer, it means x ∈ {…, -5, -4, -3, -2, -1}.
From (1), x ∈ {-2, -1}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 12
Write open mathematical sentences, using x for the variable whose graphs would be
S Chand ICSE Maths Solutions:
(i)
From the graph, we see that the shaded arrow is left of -2 (included) and all the real numbers are taken up to -2.
Thus, required mathematical sentence is {x : x ≤ -2 and x ∈ R}.
(ii)
From the graph, we see that the shaded arrow is left of 4 (included) and all the real numbers are taken up to 4.
Thus, required mathematical sentence is {x : x ≤ 4 and x ∈ R}.
(iii)
From the graph, we see that the solid circles are at 4 and 5 and only natural numbers are taken.
Thus, required mathematical sentence is {x : 4 ≤ x ≤ 5 and x ∈ N}.
(iv)
From the graph, we see that the solid circles are at 1, 3 and 5 and only natural numbers are taken.
Thus, required mathematical sentence is {x : 1 ≤ x ≤ 5 and x ∈ N}.
(v)
From the graph, we see that the shaded arrow is right of -2 (excluded) and all the real numbers are ahead of -2.
Thus, required mathematical sentence is {x : x > -2 and x ∈ R}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 13
Answer TRUE or FALSE:
(i) If 2 – x < 0, then x > 2.
(ii) The graph of the inequations y ≤ 2x includes the origin.
S Chand ICSE Maths Solutions:
(i) 2 – x < 0 ⇒ 2 < x.
Thus, the given statement is TRUE.
(ii) On putting x = 0 and y = 0 in y ≤ 2x, we get that 0 = 0, which is true.
Thus, the given statement is TRUE.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 14
If 25 – 4x ≤ 16, then find
(i) the smallest value of x when x is real number.
(ii) the smallest values of x when x is an integer.
S Chand ICSE Maths Solutions:
25 – 4x ≤ 16 ⇒ 25 – 16 ≤ 4x ⇒ 9 ≤ 4x ⇒ x ≥ 9/4.
(i) Thus, the smallest value of x is 9/4 = 2 1/4.
(ii) The smallest integer greater than x ≥ 9/4 is 3.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 15
Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9}, find the values of x for which -3 < 2x – 1< x + 4
S Chand ICSE Maths Solutions:
Given replacement set is x ∈ {1, 2, 3, 4, 5, 6, 7, 9}.
Given inequation is -3 < 2x – 1 < x + 4.
On solving -3 < 2x – 1 ⇒ 2x > -3 + 1 ⇒ 2x > -2 ⇒ x > -1 … (1)
On solving 2x – 1 < x + 4 ⇒ 2x – x < 1 + 4 ⇒ x < 5 …(2)
From (1) and (2), we get -1 < x < 5.
Thus, the solution set of the given inequation is x ∈ {1, 2, 3, 4}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 16
Solve the inequality 2x – 10 < 3x – 15
S Chand ICSE Maths Solutions:
Given inequality is 2x – 10 < 3x – 15
⇒ 2x – 3x < 10 – 15
⇒ -x < -5
⇒ x > 5
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 17
Solve the inequation 3 – 2x ≥ x – 12, given that x ∈ N.
S Chand ICSE Maths Solutions:
Given inequation is 3 – 2x ≥ x – 12
⇒ -x – 2x ≥ -3 – 12
⇒ -3x ≥ -15
⇒ x ≤ 5
Since the replacement of x is natural number, then the solution set of the given inequation is
x ∈ {1, 2, 3, 4, 5}.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 18
x ∈ {real numbers} and -1 < 3 – 2x ≤ 7, evaluate x and represent it on number line.
S Chand ICSE Maths Solutions:
Given inequation is -1 < 3 – 2x ≤ 7
From -1 < 3 – 2x,
⇒ -1 < 3 – 2x ⇒ -1 – 3 < – 2x ⇒ -4 < -2x ⇒ 2x < 4 ⇒ x < 2 …(1)
and 3 – 2x ≤ 7
⇒ 3 – 7 ≤ 2x ⇒ -4 ≤ 2x ⇒ -2 ≤ x …(2)
On combining (1) and (2), we get -2 ≤ x < 2.
The graph of this inequation is
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 19
Find the range of values of x which satisfies and graph these values of x on number line.
S Chand ICSE Maths Solutions:
Given inequation is
On simplifying, we get
Now the graph of these values of x is as below.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 20
Solution and graph the solution set of
(a)
(b)
S Chand ICSE Maths Solutions:
(a) Given inequation is
On solving first inequation, we get 6 ≥ 2 – x ⇒ x ≥ 2 – 6 ⇒ x ≥ -4 … (1)
On solving second inequation, we get x/3 + 2 < 3 ⇒ x/3 < 3 – 2 ⇒ x/3 < 1 ⇒ x < 3 … (2)
On combining (1) and (2), we get -4 ≤ x < 3.
The graph of this inequation is
(b) Given inequation is
On solving first inequation, we get
x/2 < (6 – x)/4 ⇒ 2x < 6 – x ⇒ 3x < 6 ⇒ x < 2… (1)
On solving second inequation, we get
(2 – x)/6 < (7 – x)/9 ⇒ 3(2 – x) < 2(7 – x) ⇒ 6 – 3x < 14 – 2x ⇒ x > -8 … (2)
On combining (1) and (2), we get -8 < x < 2.
The graph of this inequation is
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 21
Find the range of values of x which satisfy
Graph these values of x on real number line.
S Chand ICSE Maths Solutions:
Given inequation is
On simplifying,we get
Graph of these values of x on number line is as below.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 22
Write down the range of real values of x for which the inequation x > 3 and -2 ≤ x < 5 are both true.
S Chand ICSE Maths Solutions:
Graphing the given inequations x > 3 and -2 ≤ x < 5 on same number line, we get
Thus, we get 3 < x < 5.
S Chand ICSE Solutions for Class 10 Maths Exercise 4: Ques No 23
Solve and graph the solution set of 3x – 4 > 11 or 5 – 2x ≥ 7; x ∈ R.
S Chand ICSE Maths Solutions:
On solving the first inequation, we get 3x – 4 > 11 ⇒ 3x > 15 ⇒ x > 5 …(1)
On solving the second inequation, we get 5 – 2x ≥ 7 ⇒ – 2x ≥ 2 ⇒ x ≤ 1 …(2)
On combining (1) and (2), we get x ≤ 1 or x > 5.