S Chand ICSE Maths Solutions for Class 10 Chapter 4 Linear Inequations in One Variables
Hi students, Welcome to Amans Maths Blogs (AMB). In this post, you will get S Chand ICSE Maths Solutions for Class 10 Chapter 4 Linear Inequations in One Variable Reviosion Exercise. This is the fourth chapter ‘Linear Inequations in One Variables‘ included in ICSE 2020 Class 10 Maths syllabus.
Read : Linear Inequalities Class 10 ICSE Maths Notes PDF
S Chand ICSE Maths Solutions for Class 10 Chapter 4 Revision Exercise
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 1
Solve the following inequation and graph the solution on set on number line.
2x – 3 < x + 2 ≤ 3x + 5, x ∈ R.
S Chand ICSE Maths Solutions:
Given that 2x – 3 < x + 2 ≤ 3x + 5. Then
Inequation 1: 2x – 3 < x + 2 ⇒ 2x – x < 3 + 2 ⇒ x < 5 …(1)
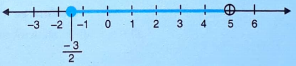
Inequation 2: x + 2 ≤ 3x + 5 ⇒ 2 – 5 ≤ 3x – x ⇒ 2x ≥ -3 ⇒ x ≥ -3/2 …(2)
From (1) and (2), we get -3/2 ≤ x < 5.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 2
Solve the inequation : 12 + 1 5/6 x ≤ 5 + 3x, x ∈ R. Represent the solution on number line.
S Chand ICSE Maths Solutions:
Given that 12 + 1 5/6 x ≤ 5 + 3x. Then
12 + 11x/6 ≤ 5 + 3x ⇒ 11x/6 – 3x ≤ 5 – 12 ⇒ -7x/6 ≤ -7 ⇒ x ≥ 6
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 3
Solve the inequation : -3 ≤ 3 – 2x < 9, x ∈ R. Represent the solution on number line.
S Chand ICSE Maths Solutions:
Given that -3 ≤ 3 – 2x < 9. Then
Inequation 1: -3 ≤ 3 – 2x ⇒ 2x ≤ 3 + 3 ⇒ 2x ≤ 6 ⇒ x ≤ 3 …(1)
Inequation 2: 3 – 2x < 9 ⇒ – 2x < 9 – 3 ⇒ – 2x < 6 ⇒ x > -3 …(2)
From (1) and (2), we get -3 < x ≤ 3.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 4
Find the value of x which satisfies the inequation: -2 ≤ 1/2 – 2x/3 ≤1 5/6, x ∈ N. Graph the solution on number line.
S Chand ICSE Maths Solutions:
Given that -2 ≤ 1/2 – 2x/3 ≤1 5/6. Then
Inequation 1: -2 ≤ 1/2 – 2x/3 ⇒ 2x/3 ≤ 1/2 + 2 ⇒ 2x/3 ≤ 5/2 ⇒ x ≤ 15/4 …(1)
Inequation 2: 1/2 – 2x/3 ≤ 1 5/6 ⇒ – 2x/3 ≤ 11/6 – 1/2 ⇒ – 2x/3 ≤ 4/3 ⇒ x ≥ -2 …(2)
From (1) and (2), we get -2 ≤ x ≤ 15/4. Since x ∈ N, x = 1, 2, 3.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 5
Solve the following inequation and graph the solution on set on number line.
2x – 5 ≤ 5x + 4 < 11, x ∈ R
S Chand ICSE Maths Solutions:
Given that 2x – 5 ≤ 5x + 4 < 11. Then
Inequation 1: 2x – 5 ≤ 5x + 4 ⇒ 2x – 5x ≤ 4 + 5 ⇒ -3x ≤ 9 ⇒ x ≥ -3 …(1)
Inequation 2: 5x + 4 < 11 ⇒ 5x ≤ 11 – 4 ⇒ 5x ≤ 7 ⇒ x ≤ 7/5 …(2)
From (1) and (2), we get -3 ≤ x ≤ 7/5.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 6
Solve 2 ≤ 2x – 3 ≤ 5, x ∈ R and mark it on number line.
S Chand ICSE Maths Solutions:
Given that 2 ≤ 2x – 3 ≤ 5. Then
Inequation 1: 2 ≤ 2x – 3 ⇒ 2 + 3 ≤ 2x ⇒ 5 ≤ 2x ⇒ x ≥ 5/2 …(1)
Inequation 2: 2x – 3 ≤ 5 ⇒ 2x ≤ 5 + 3 ⇒ 2x ≤ 8 ⇒ x ≤ 4 …(2)
From (1) and (2), we get 5/2 ≤ x ≤ 4.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 7
Given that x ∈ I (Integer), solve the inequation and graph the solution on the number line, 3 ≥ (x – 4)/2 + x / 3 ≥ 2.
S Chand ICSE Maths Solutions:
Given that 3 ≥ (x – 4)/2 + x / 3 ≥ 2 ⇒ 2 ≤ (x – 4)/2 + x / 3 ≤ 3. Then
Inequation 1: 2 ≤ (x – 4)/2 + x / 3 ⇒ 2 ≤ (3x – 12 + 2x) / 6 ⇒ 12 ≤ 5x – 12 ⇒ 24 ≤ 5x ⇒ x ≥ 24/5 …(1)
Inequation 2: (x – 4)/2 + x / 3 ≤ 3 ⇒ (5x – 12)/6 ≤ 3 ⇒ 5x ≤ 18 + 12 ⇒ x ≤ 6 …(2)
From (1) and (2), we get 24/5 ≤ x ≤ 6. Since x ∈ I (Integer), x = 5, 6.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 8
Given that x ∈ R, solve the following inequality and graph the solution on the number line, -1 ≤ 3 + 4x < 23.
S Chand ICSE Maths Solutions:
Given that -1 ≤ 3 + 4x < 23. Then
Inequation 1: -1 ≤ 3 + 4x ⇒ -1 – 3 ≤ 4x ⇒ -4 ≤ 4x ⇒ x ≥ -1 …(1)
Inequation 2: 3 + 4x < 23 ⇒ 4x < 20 ⇒ x < 5 …(2)
From (1) and (2), we get -1 ≤ x < 5.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 9
Solve the following inequation and graph the solution on the number line -2 2/3 ≤ x + 1/3 < 3 1/3, x ∈ R.
S Chand ICSE Maths Solutions:
Given that -2 2/3 ≤ x + 1/3 < 3 1/3. Then
Inequation 1: -2 2/3 ≤ x + 1/3 ⇒ -8/3 ≤ x + 1/3 ⇒ -9/3 ≤ x ⇒ x ≥ -3 …(1)
Inequation 2: x + 1/3 < 3 1/3 ⇒ x < 10/3 – 1/3 ⇒ x < 3 …(2)
From (1) and (2), we get -3 ≤ x < 3.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 10
Solve the given inequation and graph the solution on the number line 2y – 3 ≤ y + 1 < 4y + 7, y ∈ R.
S Chand ICSE Maths Solutions:
Given that 2y – 3 ≤ y + 1 < 4y + 7. Then
Inequation 1: 2y – 3 ≤ y + 1 ⇒ 2y – y ≤ 1 + 3 ⇒ y ≤ 4 …(1)
Inequation 2: y + 1 < 4y + 7 ⇒ y – 4y < 7 – 1 ⇒ -3y < 6 ⇒ y > -2 …(2)
From (1) and (2), we get -2 < y ≤ 4.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 11
Solve the given inequation and represent the solution on the number line -3 + x ≤ 8x/3 + 2 ≤ 14/3 + 2x, where x ∈ I.
S Chand ICSE Maths Solutions:
Given that -3 + x ≤ 8x/3 + 2 ≤ 14/3 + 2x. Then
Inequation 1: -3 + x ≤ 8x/3 + 2 ⇒ x – 8x/3 ≤ 2 + 3 ⇒ -5x/3 ≤ 5 ⇒ x ≥ -3 …(1)
Inequation 2: 8x/3 + 2 ≤ 14/3 + 2x ⇒ 8x/3 – 2x ≤ 14/3 – 2 ⇒ 2x/3 ≤ 8/3 ⇒ x ≤ 4 …(2)
From (1) and (2), we get -3 ≤ x ≤ 4. Since x ∈ I, x = -3, -2, -1, 0, 1, 2, 3, 4.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 12
Solve the given inequation and represent the solution on the number line -3 < – 1/2 – 2x/3 ≤ 5/6, where x ∈ R.
S Chand ICSE Maths Solutions:
Given that -3 < – 1/2 – 2x/3 ≤ 5/6. Then
Inequation 1: -3 < – 1/2 – 2x/3 ⇒ 2x/3 ≤ -1/2 + 3 ⇒ 2x/3 ≤ 5/2 ⇒ x ≤ 15/4 …(1)
Inequation 2: – 1/2 – 2x/3 ≤ 5/6 ⇒ -2x/3 ≤ 5/6 + 1/2 ⇒ -2x/3 ≤ 8/6 ⇒ x ≥ -2 …(2)
From (1) and (2), we get -2 ≤ x ≤ 15/4.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 13
Solve the given inequation and represent the solution on the number line 2x – 5 ≤ 5x + 4 < 11, where x ∈ I.
S Chand ICSE Maths Solutions:
Given that 2x – 5 ≤ 5x + 4 < 11. Then
Inequation 1: 2x – 5 ≤ 5x + 4 ⇒ 2x – 5x ≤ 5 + 4 ⇒ -3x ≤ 9 ⇒ x ≥ -3 …(1)
Inequation 2: 5x + 4 < 11 ⇒ 5x < 11 – 4 ⇒ 5x < 7 ⇒ x < 7/5 …(2)
From (1) and (2), we get -3 ≤ x < 7/5. Since x ∈ I, so x = -3, -2, -1, 0, 1.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 14
Solve the given inequation and represent the solution on the number line 4x – 19 < 3x/5 – 2 ≤ -2/5 + x, where x ∈ R.
S Chand ICSE Maths Solutions:
Given that 4x – 19 < 3x/5 – 2 ≤ -2/5 + x. Then
Inequation 1: 4x – 19 < 3x/5 – 2 ⇒ 4x – 3x/5 ≤ 19 – 2 ⇒ 17x/5 ≤ 17 ⇒ x ≤ 5 …(1)
Inequation 2: 3x/5 – 2 ≤ -2/5 + x ⇒ 3x/5 – x ≤ -2/5 + 2 ⇒ -2x/5 ≤ 8/5 ⇒ x ≥ -4 …(2)
From (1) and (2), we get -4 ≤ x ≤ 5.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 15
Solve the given inequation and represent the solution on the number line -x/3 ≤ x/2 – 1 1/3 < 1/6, where x ∈ R.
S Chand ICSE Maths Solutions:
Given that -x/3 ≤ x/2 – 1 1/3 < 1/6. Then
Inequation 1: -x/3 ≤ x/2 – 1 1/3 ⇒ -x/3 – x/2 ≤ -4/3 ⇒ -5x/6 ≤ -4/3 ⇒ x ≥ 8/5 ⇒ x ≥ 1.6 …(1)
Inequation 2: x/2 – 1 1/3 < 1/6 ⇒ x/2 < 1/6 + 4/3 ⇒ x/2 < 9/6 ⇒ x < 3 …(2)
From (1) and (2), we get 1.6 ≤ x < 3.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 16
Find the value of x, which satisfy the inequation -2 5/6 < 1/2 – 2x/3 ≤ 2, where x ∈ W. Graph the solution set on the number line.
S Chand ICSE Maths Solutions:
Given that -2 5/6 < 1/2 – 2x/3 ≤ 2. Then
Inequation 1: -2 5/6 < 1/2 – 2x/3 ⇒ -17/6 < 1/2 – 2x/3 ⇒ 2x/3 < 1/2 + 17/6 ⇒ 2x/3 < 20/6 ⇒ x < 5 …(1)
Inequation 2: 1/2 – 2x/3 ≤ 2 ⇒ -2x/3 ≤ 2 + 1/2 ⇒ -2x/3 ≤ 5/2 ⇒ x ≥ -15/4 …(2)
From (1) and (2), we get -15/4 ≤ x < 5. Since x ∈ W, so x = 0, 1, 2, 3, 4.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 17
Solve the given inequation and represent the solution on the number line 13x – 5 < 15x + 4 < 7x + 12, where x ∈ R.
S Chand ICSE Maths Solutions:
Given that 13x – 5 < 15x + 4 < 7x + 12. Then
Inequation 1: 13x – 5 < 15x + 4 ⇒ 13x – 15x < 4 + 5 ⇒ -2x < 9 ⇒ x > -9/2 ⇒ x > -4.5 …(1)
Inequation 2: 15x + 4 < 7x + 12 ⇒ 15x – 7x < 12 – 4 ⇒ 8x < 8 ⇒ x < 1 …(2)
From (1) and (2), we get -4.5 < x < 1.
Now, the graph of the solution on number line is below.
S Chand ICSE Solutions for Class 10 Maths Linear Inequations Revision Exercise: Ques No 18
Solve the given inequation and represent the solution on the number line -3(x – 7) ≥ (15 – 7x) > (x + 1)/3, where x ∈ R.
S Chand ICSE Maths Solutions:
Given that -3(x – 7) ≥ (15 – 7x) > (x + 1)/3. Then
Inequation 1: -3(x – 7) ≥ (15 – 7x) ⇒ -3x + 21 ≥ 15 – 7x ⇒ -3x + 7x ≥ 15 – 21 ⇒ 4x ≥ -6 ⇒ x ≥ -3/2 …(1)
Inequation 2: 15 – 7x > (x + 1)/3 ⇒ 3(15 – 7x) > x + 1 ⇒ 45 – 21x > x + 1 ⇒ 44 > 22x ⇒ x < 2 …(2)
From (1) and (2), we get -3/2 ≤ x < 2.
Now, the graph of the solution on number line is below.