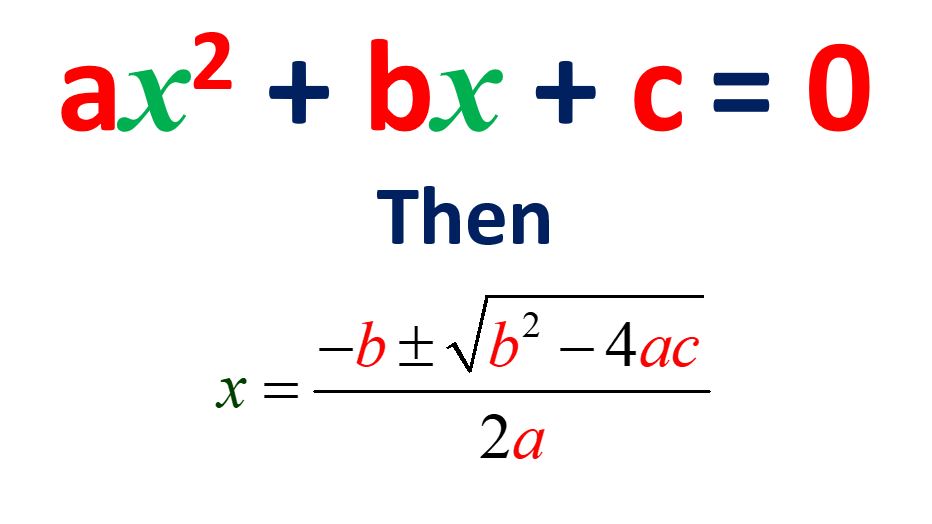Hi students, Welcome to Amans Maths Blogs (AMB). In this article, you will get Quadratic Equations Class 10 Maths Revision Notes Chapter 5 PDF.
Quadratic Polynomials
A polynomial of the form of p(x) = ax2 + bx + c is known as quadratic polynomial, where a, b, c are real and a ≠ 0.
For example: p(x) = 3x2 + 5x – 2, here a = 3, b = 5 and c = -2.
Quadratic Equations
An equation in the form of ax2 + bx + c = 0 is known as quadratic equation, where a, b, c are real and a ≠ 0.
For example: 3x2 + 5x – 2 = 0, here a = 3, b = 5 and c = -2.
Solving Quadratic Equations by Factorization
To solve a quadratic equation by factorization, we do the following steps:
Step 1 : Express the equation in the form of ax2 + bx + c = 0.
Step 2 : Factorize ax2 + bx + c using middle term splitting method.
Step 3 : Put each factor equal to zero.
Step 4 : Solve each equation.
Equations Reducible to Quadratic Equations
An equation in the form of ax2 + bx + c = 0 is known as quadratic equation, where a, b, c are real and a ≠ 0.
In some questions, the given equations are not in form of ax2 + bx + c = 0. Then, to solve such type of equations, first we need to reduce the given equation in form of quadratic equation ax2 + bx + c = 0 by using suitable algebraic transformation and then solve it.
Solving Quadratic Equation by Quadratic Formula
An equation in the form of ax2 + bx + c = 0 is known as quadratic equation, where a, b, c are real and a ≠ 0.
To solve quadratic equations, there are two methods :
2. Using Quadratic Formula
In this exercise, the quadratic equations are solved by using the quadratic formula.
Proof of Quadratic Formula
Let the quadratic equation is ax2 + bx + c = 0, where a ≠ 0. We need to find the value of x.
ax2 + bx + c = 0
⇒ ax2 + bx = – c [Transposing constant term c to RHS]
⇒ x2 + (b/a)x = – c/a [Dividing both sides by a to make coefficient of x2 = 1]
⇒ x2 + (b/a)x + b2/4a2 = b2/4a2 – c/a [Adding both sides by b2/4a2]
⇒ x2 + 2(b/2a)x + b2/4a2 = (b2 – 4ac)/4a2
⇒ (x + b/2a)2 = (b2 – 4ac)/4a2
⇒ (x + b/2a) = ± √(b2 – 4ac)/2a
⇒ x = – b/2a ± √(b2 – 4ac)/2a
⇒ x = – b ± √(b2 – 4ac)]/2a.
Therefore, if the quadratic equation ax2 + bx + c = 0, then the value of x is x = [- b ± √(b2 – 4ac)]/2a. This is known as Quadratic Formula.
Hence, there are two values of x as x = [- b + √(b2 – 4ac)]/2a or x = [- b + √(b2 – 4ac)]/2a.
Discriminant of Quadratic Equations
An equation in the form of ax2 + bx + c = 0 is known as quadratic equation, where a, b, c are real and a ≠ 0.
Then the value of x is x = [- b ± √(b2 – 4ac)]/2a. This is known as Quadratic Formula.
Hence, there are two values of x as x = [- b + √(b2 – 4ac)]/2a or x = [- b + √(b2 – 4ac)]/2a.
Now, in x = [- b ± √(b2 – 4ac)]/2a, the term under square root, that is (b2 – 4ac) is known as the discriminant of the quadratic equation of ax2 + bx + c = 0 and it is denoted by D.
Thus, D = b2 – 4ac.
Nature of Roots of Quadratic Equations
The nature of the roots determines the types of the roots of quadratic equation of ax2 + bx + c = 0, whether the roots are real or imaginary and if the roots are real, then it will be rational or irrational and equal or unequal.
Since D = b2 – 4ac is in quadratic formula x = [- b ± √(b2 – 4ac)]/2a, then the value of the discriminant D = b2 – 4ac determines the nature of the roots of quadratic equations.
You don’t need to solve the quadratic equation of ax2 + bx + c = 0. You just need to find the value of its discriminant D = b2 – 4ac.
How To Determine Nature of Roots of Quadratic Equations
If the discriminant D = b2 – 4ac is positive (means, D > 0), then the roots of quadratic equation are REAL and DISTINCT.
If the discriminant D = b2 – 4ac is positive and perfect square, then the roots of quadratic equation are REAL, RATIONAL and DISTINCT.
If the discriminant D = b2 – 4ac is positive and NOT a perfect square, then the roots of quadratic equation are REAL, IRRATIONAL and DISTINCT.
If the discriminant D = b2 – 4ac is zero (means, D = 0), then the roots of quadratic equation are REAL and EQUAL. And, Root will be α = β = -b/2a.
If the discriminant D = b2 – 4ac is negative (means, D < 0), then the roots of quadratic equation are NOT REAL , it means the roots are IMAGINARY.
Summary of the nature of the roots of quadratic equation is as below.
Quadratic Equations Word Problems
In word problems, first we need to make a quadratic equation according to the given question and then we need to solve them.
Read : S Chand Class 10 ICSE Maths Quadratic Equations Exercise 5A Solutions PDF
Read : S Chand Class 10 ICSE Maths Quadratic Equations Exercise 5B Solutions PDF
Read : S Chand Class 10 ICSE Maths Quadratic Equations Exercise 5C Solutions PDF
Read : S Chand Class 10 ICSE Maths Quadratic Equations Exercise 5D Solutions PDF
Read : S Chand Class 10 ICSE Maths Quadratic Equations Exercise 5E Solutions PDF
Read : S Chand Class 10 ICSE Maths Quadratic Equations Revision Exercise Solutions PDF