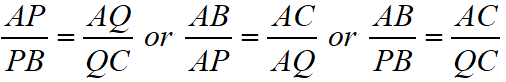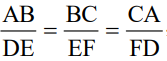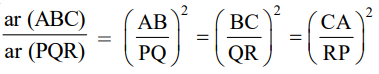Hi students, Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get Similar Triangles CBSE NCERT Notes Class 10 Maths Chapter 6 PDF. You can download this PDF and save it in your mobile device or laptop etc.
Similar Triangles CBSE NCERT Notes Class 10 Maths Chapter 6 PDF
Similar Figures
Two figures having the same shape (and not necessarily the same size) are called similar figures.
Two similar figures have the same shape but not necessarily the same size.
Therefore, all circles are similar. all squares are similar and all equilateral triangles are similar.
All congruent figures are similar but the similar figures need not be congruent.
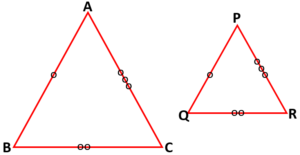
Two polygons of the same number of sides are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).
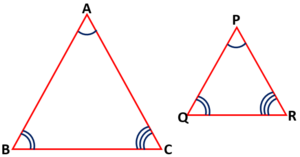
Similar Triangles
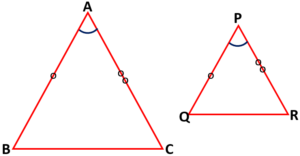
Two triangles are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).
Similar triangles are also called equiangular triangles.
Basic Proportionality Theorem (BPT) or Theles Theorem
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
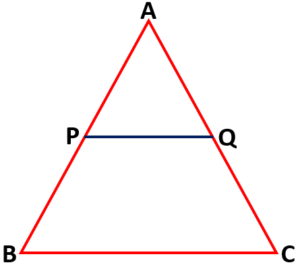
Thus, in triangle ABC, if PQ || BC, then
Class 10 Maths Chapter 6 Examples 1:
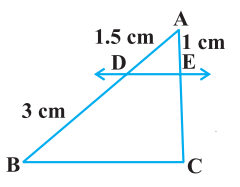
Find the value of EC in the figure below, if DE || BC.
Using BPT, we have AD/DB = AE/EC.
Since AD = 1.5, DB = 3 and AE = 1.
Then, 1.5/3 = 1/EC ⇒ EC = 2
Criteria for Similarity Triangles
Two triangles are similar, if (i) their corresponding angles are equal and (ii) their corresponding sides are in the same ratio (or proportion).
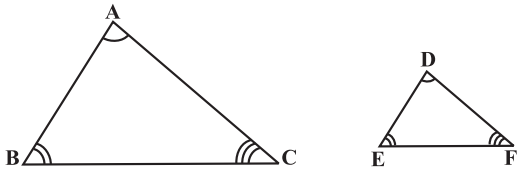
In Δ ABC and Δ DEF, if
(i) ∠ A = ∠ D, ∠ B = ∠ E, ∠ C = ∠ F and
(ii)
then the two triangles are similar.
Based on these, there are three criteria for similarity of triangles
| Similar Triangles Criteria | |||||||
|---|---|---|---|---|---|---|---|
| SSS | The corresponding sides of two triangles are proportional. | ||||||
| SAS | One pair of corresponding sides are proportional and the included angles are equal. | ||||||
| AA | Two triangles are equiangular. | ||||||
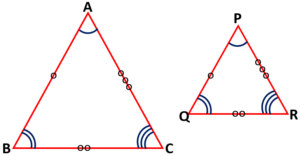
AAA or AA (Angle-Angle) Similarity
If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.
In Δ ABC and Δ PQR, if ∠ A = ∠ P and ∠ B = ∠ Q,
then Δ ABC and Δ PQR are similar (ΔABC ~ Δ PQR).
And hence, we have result AB/PQ = BC/QR = AC/PR.
Class 10 Maths Chapter 6 Examples 2:
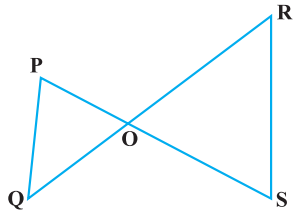
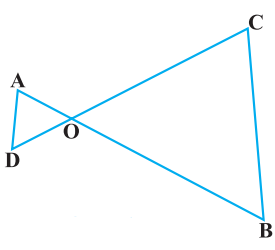
In the given figure below, if PQ || RS, prove that Δ POQ ~ Δ SOR.
Since ∠POQ = ∠SOR (vertically opposite angles are equal) and ∠QPO = ∠RSO (alternate angles are equal), by AA similarity, we get Δ POQ ~ Δ SOR.
SSS (Side-Side-Side) Similarity
If in two triangles, sides of one triangle are proportional to (i.e., in the same ratio of ) the sides of the other triangle, then their corresponding angles are equal and hence the two triangles are similar.
In Δ ABC and Δ PQR, if AB/PQ = BC/QR = AC/PR,
then Δ ABC and Δ PQR are similar (ΔABC ~ Δ PQR).
And hence, we have result ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R.
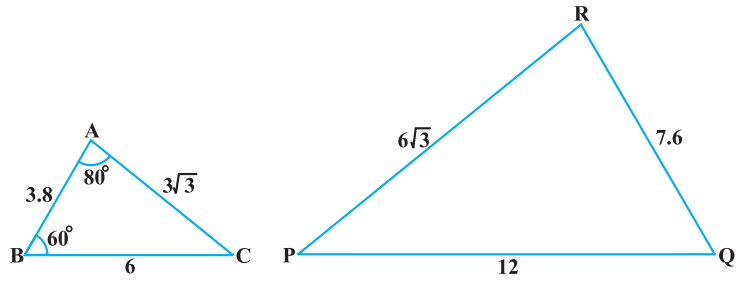
Class 10 Maths Chapter 6 Examples 3:
In the given figure below, find ∠ P.
Since
Thus, ∠ P = ∠ C = 180° – ∠ A – ∠ B = 180° – 80° – 60° = 40°
SAS (Side-Angle-Side) Similarity
If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional, then the two triangles are similar.
In Δ ABC and Δ PQR, if ∠A = ∠P and AB/PQ = AC/PR,
then Δ ABC and Δ PQR are similar (ΔABC ~ Δ PQR).
And hence, we have result , ∠B = ∠Q, ∠C = ∠R and AB/PQ = BC/QR = AC/PR.
Class 10 Maths Chapter 6 Examples 4:
In the given figure below, if OA . OB = OC . OD, then prove that ∠ A = ∠ C and ∠ B = ∠ D.
Since OA . OB = OC . OD ⇒ OA / OC = OD / OB and ∠ AOD = ∠ COB (Vertically opposite angles).
By SAS similarity, we get Δ AOD ~ Δ COB. Thus, ∠ A = ∠ C and ∠ D = ∠ B.
Area of Similar Triangles
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Since it is given two triangles ABC and PQR such that Δ ABC ~ Δ PQR, then
Class 10 Maths Chapter 6 Examples 5:
If the sides of two similar triangles are in the ratio 4 : 9, then find the ratio of areas of these triangles.
Required ratio = √(4/9) = 4/3
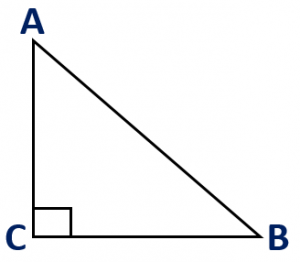
Pythagorus Theorem
If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In right triangle ABC with C = 90 degree, AB2 = AC2 + BC2.
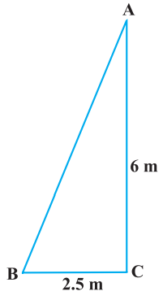
Class 10 Maths Chapter 6 Examples 6:
A ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall and its top reaches a window 6 m above the ground. Find the length of the ladder.
From Pythagoras Theorem, we have
AB2 = BC2 + CA2 = (2.5)2 + (6)2 = 42.25 ⇒ AB = 6.5
Click below to get CBSE Class 10 Maths Chapter wise Revision Notes PDF.