Hi students, Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get Areas Related to Circles CBSE NCERT Notes Class 10 Maths Chapter 12 PDF. You can download this PDF and save it in your mobile device or laptop etc.

Areas Related to Circles CBSE NCERT Notes Class 10 Maths Chapter 12 PDF

Perimeter or Circumference of Circle

The circumference of a circle whose radius is r is C = 2πr.

Class 10 Maths Chapter 12 Examples 1:

The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.

Given that r₁ = 19 and r₂ = 9.

Now, C = C₁ + C₂ ⇒ 2πr = 2πr₁ + 2πr₂ ⇒ r = r₁ + r₂ = 28 cm.

Area of Circle

The area of a circle with radius r is A = πr².

Class 10 Maths Chapter 12 Examples 2:

The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.

Given that r₁ = 8 and r₂ = 6.

Now, A = A₁ + A₂ ⇒ πr² = πr₁² + πr₂²

⇒ r² = r₁² + r₂² ⇒ r² = 64 + 36 = 100 ⇒ r = 10 cm

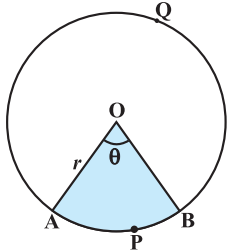
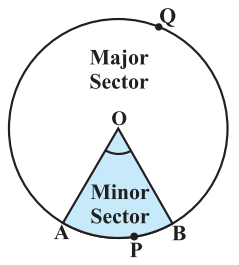
Sector of Circle

The portion of the circular region enclosed by two radii and the corresponding arc is called a sector of the circle.

Shaded region OAPB is a sector of the circle with centre O and ∠ AOB is called the angle of the sector.

Unshaded region OAQB is also a sector of the circle.

From the figure below, OAPB is called the minor sector and OAQB is called the major sector

Area of Sector of Circle

Area of sector of a circle with radius r is πr²θ/360^o.

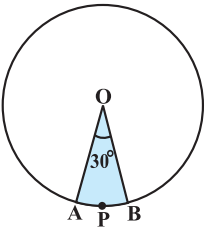
Class 10 Maths Chapter 12 Examples 3:

Find the area of the sector of a circle with radius 4 cm and of angle 30°. 

Required area of sector of Circle = πr²θ/360^o = 3.14 × 16 × 30/360 = 4.19 cm².  

Length of Arc of Sector of Circle

Length of an arc of sector of a circle with radius r is 2πrθ/360^o.

Class 10 Maths Chapter 12 Examples 4:

In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find the length of the arc.

Length of an arc of sector of a circle with radius L = 2πrθ/360^o = 2 × 22/7 × 21 × 60 / 360 = 22 cm.

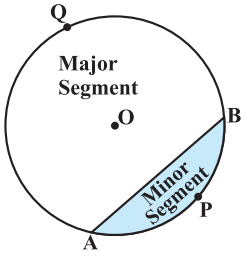
Segment of Circle

The portion of the circular region enclosed between a chord and the corresponding arc is called a segment of the circle.

Shaded region APB is a segment of the circle with centre O.

Unshaded region AQB is also a segment of the circle.

From the figure below, APB is called the minor segment and AQB is called the major segment.

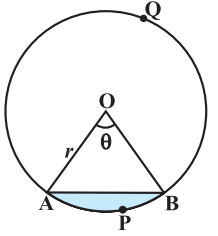
Area of Segment of Circle

Area of the segment APB

= Area of the sector OAPB – Area of Δ OAB

= πr²θ/360^o – (r²sinθ)/2

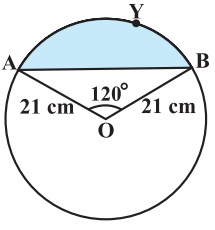
Class 10 Maths Chapter 12 Examples 5:

Find the area of the segment AYB as shown in figure below. 

Area of the segment AYB

= Area of sector OAYB – Area of Δ OAB

= πr²θ/360^o – (r²sinθ)/2

= 22/7 × 21 × 21 × 120/360 – (21 × 21 × sin120)/2

= 462 – (441 × √3 / 2)/2

= 462 – 441√3/4

Area of Combination of Plane Figures

In this, we need to find the area of shaded regions. 

Class 10 Maths Chapter 12 Examples 6:

Find the area of the shaded region in figure below, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.  

Using Pythagoras theorem, QR² = PQ² + RP² = 576 + 49 = 625

⇒ QR = 25 ⇒ Radius of circle, r = QR/2 = 25/2  

Shaded region = Area of Semi-Circle – Area of Right Angle Triangle

= πr²/2 – 1/2 × 24 × 7

= 625π/2 – 91

Click below to get CBSE Class 10 Maths Chapter wise Revision Notes PDF.