Hi students, Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get Surface Areas and Volumes CBSE NCERT Notes Class 10 Maths Chapter 13 PDF. You can download this PDF and save it in your mobile device or laptop etc.
Surface Areas and Volumes CBSE NCERT Notes Class 10 Maths Chapter 13 PDF
Cuboid
There are following formulas for cuboid.
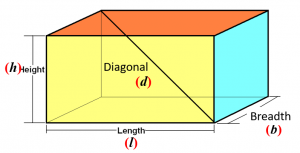
1. Lateral Surface Area (LSA) = 2h(l + b)
2. Total Surface Area (TSA) = 2(lb + bh + hl)
3. Volume (V) = lbh
4. Diagonal (d) = √(l2 + b2 + h2)
Class 10 Maths Chapter 13 Examples 1:
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs 10 per m2 is Rs 15000, find the height of the hall.
Area of Four walls = 15000/10 = 1500
⇒ 2h(l + b) = 1500
⇒ h × 250 = 1500
⇒ h = 1500/250 = 6 m
Cube
There are following formulas for cube.
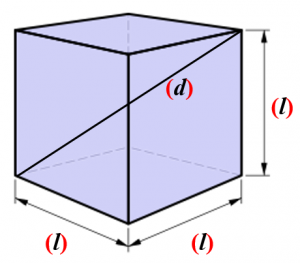
1. Lateral Surface Area (LSA) = 4l2
2. Total Surface Area (TSA) = 6l2
3. Volume (V) = l3
4. Diagonal (d) = l√3
Class 10 Maths Chapter 13 Examples 2:
A cubical box has each edge 10 cm. Find the length of its diagonal.
Since l = 10. Thus, the length of the diagonal is d = 10√3.
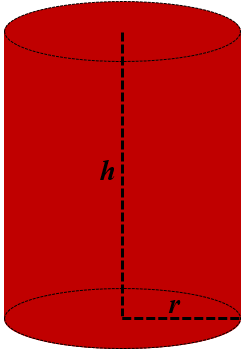
Cylinder (Closed at Both Ends)
There are following formulas for cylinder, which are closed at both ends.
1. Curved Surface Area (CSA) = 2πrh
2. Total Surface Area (TSA) = 2πrh + πr2 + πr2 = 2πr(h + r)
3. Volume (V) = πr2h
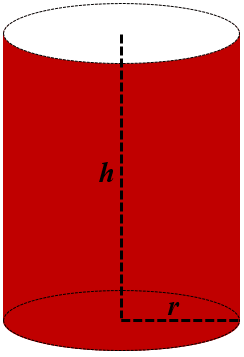
Cylinder (Open at Top)
There are following formulas for cylinder which are open at both ends.
1. Curved Surface Area (CSA) = 2πrh
2. Total Surface Area (TSA) = 2πrh + πr2 = πr(2h + r)
3. Volume (V) = πr2h
Hollow Cylinder (Open at Both Ends)
There are following formulas for cylinder which are open at both ends (example: Pipe).
1. External Curved Surface Area (ECSA) = 2πRh
2. Internal Curved Surface Area (ICSA) = 2πrh
3. Circular Area of Top or Bottom = π(R2 – r2)
4. Total Surface Area (TSA) = 2πRh + 2πrh + 2π(R2 – r2) = πr(2h + r)
5. Volume (V) = πR2h – πr2h
Class 10 Maths Chapter 13 Examples 3:
The curved surface area of a right circular cylinder of height 14 cm is 88 cm2. Find the diameter of the base of the cylinder.
Since CSA = 88
⇒ 2πrh = 88
⇒ 2 × 22/7 × r × 14 = 88
⇒ r = 1
Thus, required diameter of the cylinder is d = 2r = 2 cm.
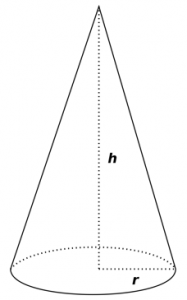
Cone
There are following formulas for cone.
1. Slant height (l) = √(r2 + h2)
2. Curved Surface Area (CSA) = πrl
3. Total Surface Area (TSA) = πrl + πr2 = πr(l + r)
4. Volume (V) = (1/3)πr2h
Class 10 Maths Chapter 13 Examples 4:
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 28 m.
Since l = 21 and r = d/2 = 14
Thus, TSA = πr(l + r) = 22/7 × 12 × (21 + 14) = 22 × 12 × 5 = 1320 m2.
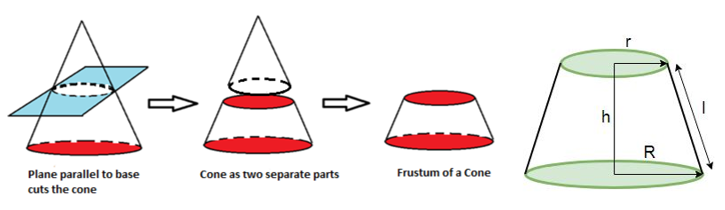
Frustum of Cone
There are following formulas for cone.
1. Slant height (l) = √(h2 + (R – r)2)
2. Curved Surface Area (CSA) = π(R + r)l
3. Total Surface Area (TSA) = π(R + r)l + πr2 + πR2
4. Volume (V) = (1/3)π(R2 + r2 + rR)h
Class 10 Maths Chapter 13 Examples 5:
Find the volume of the frustum of cone whose base and top radius is 5 mm and 2 mm respectively. The height of the frustum of cone is 15 mm.
Volume (V) = (1/3)π(R2 + r2 + rR)h = 1/3 × 22/7 × (25 + 4 + 10) × 15 = 612.3 mm2.
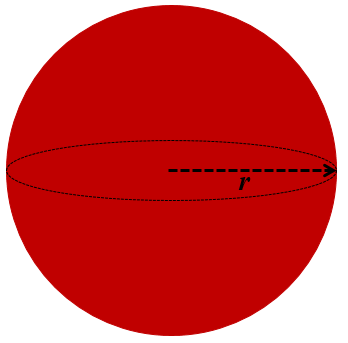
Sphere
There are following formulas for sphere.
1. Surface Area (SA) = 4πr2
2. Volume (V) = (4/3)πr3
Class 10 Maths Chapter 13 Examples 6:
Find the surface area of a sphere of radius 7 cm
SA = 4πr2 = 4 × 22/7 × 7 × 7 = 616 cm2.
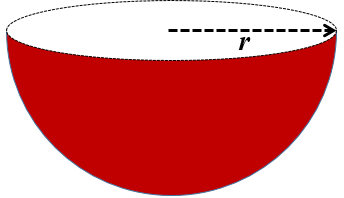
Hemi-Sphere
There are following formulas for hemisphere.
1. Curved Surface Area (CSA) = 2πr2
2. Total Surface Area (TSA) = 3πr2
3. Volume (V) = (2/3)πr3
Class 10 Maths Chapter 13 Examples 7:
Find the volume of a hemisphere of radius 7 cm
V = (2/3)πr3 = 4/3 × 22/7 × 7 × 7 × 7 = 718.66 cm3.
Combination of Solids
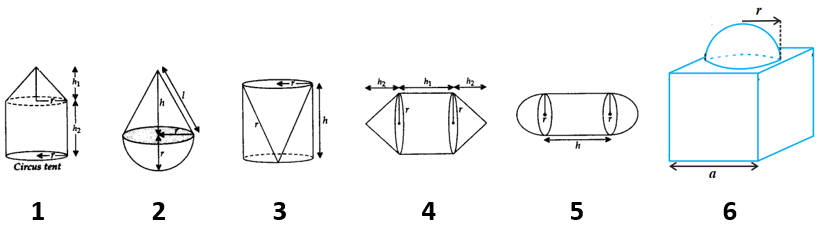
If two or more solids are combined. Here, you will get some examples of combination of solids.
Surface Areas of Combination of Above Solids
For Solid Figure 1 : Cone on Cylinder
TSA of Solid 1 = CSA of Cone + CSA of Cylinder + Area of Circular Base = πrl + 2πrh2 + πr2
For Solid Figure 2 : Cone on Hemisphere
TSA of Solid 2 = CSA of Cone + CSA of Hemisphere = πrl + 2πr2
For Solid Figure 3 : Conical Cavity in Cylinder
TSA of Solid 3 = CSA of Cylinder + Area of Base of Cylinder + CSA of Cone = 2πrh + πr2 + πrl
For Solid Figure 4 : Cones on Both Ends of Cylinder
TSA of Solid 4 = CSA of Two Cones + CSA of Cylinder = 2πrl + 2πrh1
For Solid Figure 5 : Hemispheres on Both Ends of Cylinder
TSA of Solid 5 = CSA of Two Hemispheres + CSA of Cylinder = 2πrh + 4πr2
For Solid Figure 6 : Hemispheres on Cubes
TSA of Solid 6
= TSA of Cube – Area of Hemisphere Face + CSA of Hemisphere = 6a2 – πr2 + 2πr2 = 6a2 + πr2
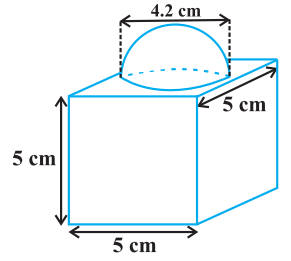
Class 10 Maths Chapter 13 Examples 8:
Find the total surface area of the solids given as below.
Surface Area
= TSA of Cube – Base Area of Hemisphere + CSA of Hemisphere
= (6 × 5 × 5) – πr2 + 2πr2
= (150 + πr2)
= 150 + 22/7 × 4.2/2 × 4.2/2
= 163.86 cm2.
Volumes of Combination of Above Solids
For Solid Figure 1 : Cone on Cylinder
Volume of Solid 1 = Volume of Cone + Volume of Cylinder = (1/3)πr2h1 + πr2h2
For Solid Figure 2 : Cone on Hemisphere
Volume of Solid 2 = Volume of Cone + Volume of Hemisphere = (1/3)πr2h + (4/3)πr3
For Solid Figure 3 : Conical Cavity in Cylinder
Volume of Solid 3 = Volume of Cylinder – Volume of Cone = πr2h – (1/3)πr2h = (2/3)πr2h
For Solid Figure 4 : Cones on Both Ends of Cylinder
Volume of Solid 4 = Volume of Two Cones + Volume of Cylinder = (2/3)πr2h2 + πr2h1
For Solid Figure 5 : Hemispheres on Both Ends of Cylinder
Volume of Solid 5 = Volume of Two Hemisphere + Volume of Cylinder = (4/3)πr3 + πr2h
For Solid Figure 6 : Hemispheres on Cubes
Volume of Solid 6 = Volume of Cube + Volume of Hemisphere = a3 + (4/3)πr3
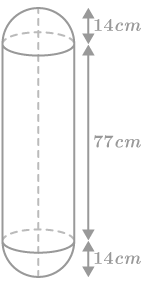
Class 10 Maths Chapter 13 Examples 9:
A solid is composed of a cylinder with hemispherical ends. If the total height of the solid is 105 cm and the radius of the hemispherical ends is 14 cm, find the volume of the solid.
Radius of the hemispherical ends = radius of the cylinder = 14 cm.
Volume = Volume of Two Hemisphere + Volume of Cylinder
= (4/3)πr3 + πr2h
= (4/3) × 22/7 × 143 + 22/7 × 142 × 77
= 22/7 × 14 × 14 × [4/3 × 14 + 77]
= 44 × 14 × 287/3
= 58930.67 cm3.
Click below to get CBSE Class 10 Maths Chapter wise Revision Notes PDF.