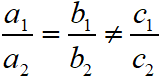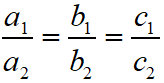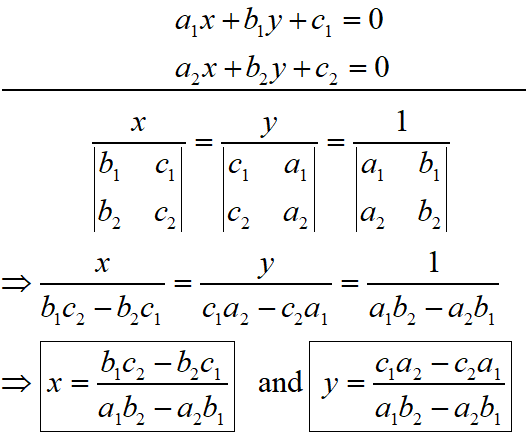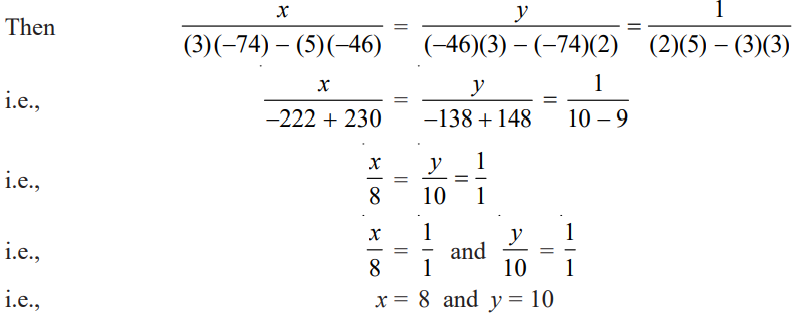Hi students, Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get Pair of Linear Equations in Two Variables CBSE Notes Class 10 Maths Chapter 3 PDF. You can download this PDF and save it in your mobile device or laptop etc.
Pair of Linear Equations in Two Variables CBSE Notes Class 10 Maths Chapter 3
Linear Equation in Two Variables
An equation in the form of ax + by + c = 0, where a, b and c are real numbers, and a and b are not both zero, is called a linear equation in two variables x and y.
The graph of a linear equation is a straight line.
Every solution of the linear equation is a point on the line representing it.
Each solution (x, y) of a linear equation in two variables, ax + by + c = 0, corresponds to a point on the line representing the equation, and vice versa.
Class 10 Maths Chapter 3 Examples 1:
Check whether the point (1, 1) lies on the line represented by the linear equation 2x + 3y = 5.
Put x = 1 and y = 1 in LHS of the given equation.
LHS = 2(1) + 3(1) = 2 + 3 = 5 = RHS.
Thus, the point (1, 1) lies on the line 2x + 3y = 5.
Class 10 Maths Chapter 3 Examples 2:
Check whether the point (1, 7) lies on the line represented by the linear equation 2x + 3y = 5.
Put x = 1 and y = 2 in LHS of the given equation.
LHS = 2(1) + 3(2) = 2 + 6 = 8 ≠ RHS.
Thus, the point (1, 7) does not lie on the line 2x + 3y = 5.
Linear Equation in Two Variables
The standard form of linear equations is
a1x + b1y + c1 = 0 and
a2x + b2y + c2 = 0.
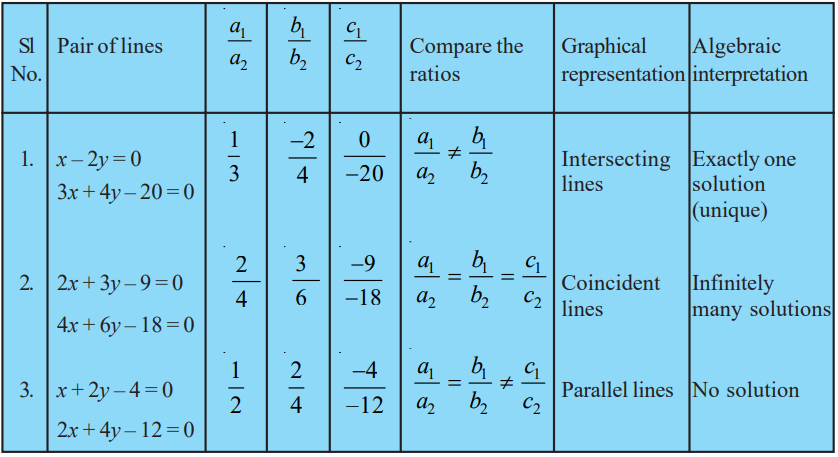
Condition of Solvability
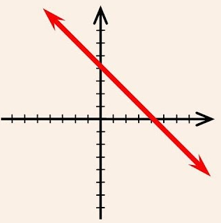
For Unique Solution (Only One Solution) or Consistent System of Equations, in this case the graph of the linear equations is intersected lines.
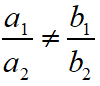
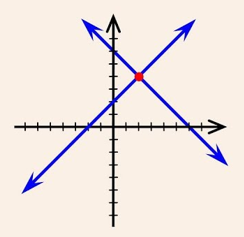
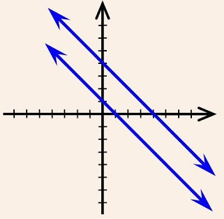
For No Solution or Inconsistent System of Equations, in this case the graph of the linear equations is parallel lines.
For Many Solution or Consistent System of Equations, in this case the graph of the linear equations is coincident lines.
Class 10 Maths Chapter 3 Examples 3:
What kind of pair of the following linear equations are geometrically?
(1) x – 2y = 0 and 3x + 4y – 20 = 0
(2) 2x + 3y – 9 = 0 and 4x + 6y – 18 = 0
(3) x + 2y – 4 = 0 and 2x + 4y – 12 = 0
Graphical Method of Solving of Linear Equation in Two Variables
The standard form of linear equations is a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0.
In graphical method, the graphs of the linear equations are drawn and the solution of the linear equations is the point where both the graph of linear equations are intersect each other if they are consistent.
Class 10 Maths Chapter 3 Examples 4:
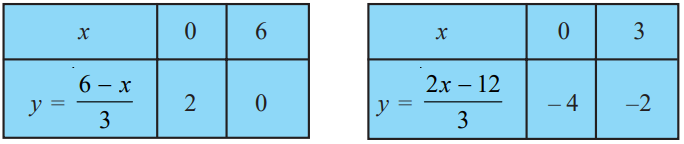
Solve the following linear of equation in two variables by graphical method:
x + 3y = 6 and 2x – 3y = 12
To drawn the graph of the given linear equations, we need to make a table as below.
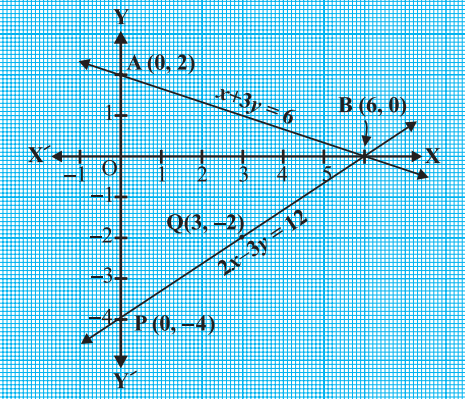
Plot the points A(0, 2), B(6, 0), P(0, – 4) and Q(3, – 2) on graph paper, and join the points to form the lines AB and PQ as shown in figure below.
We observe that there is a point B (6, 0) common to both the lines AB and PQ.
So, the solution of the pair of linear equations is x = 6 and y = 0.
Algebraic Method of Solving of Linear Equation in Two Variables
The standard form of linear equations is a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0.
These two equations can be solved by method of substitutions, elimination and cross multiplications.
Let understand it by examples
Class 10 Maths Chapter 3 Examples 5:
Solve the following pair of equations by substitution method
7x – 15y = 2 …(1)
and x + 2y = 3 …(2)
From (2), we get x = 3 – 2y … (3)
Substitute the value of x in Equation (1), we get
7(3 – 2y) – 15y = 2
⇒ 21 – 14y – 15y = 2
⇒ – 29y = –19
⇒ y = 19/29
Substituting this value of y in Equation (3), we get x = 49/29.
Thus, the solution of the given equations is x = 49/29 and y = 19/29.
Class 10 Maths Chapter 3 Examples 6:
Solve the following pair of equations by elimination method.
9x – 4y = 2000 …(1)
and 7x – 3y = 2000 …(2)
From (1) × 3 – (2) × 4, we get
⇒ (28x – 27x) – (12y – 12y) = 8000 – 6000
⇒ x = 2000
From (1)
9(2000) – 4y = 2000 ⇒ y = 4000.
Thus, x = 2000 and y = 4000.
Cross Multiplication Method of Solving of Linear Equation in Two Variables
The cross multiplication method for solving linear equations in two variables is as below.
Class 10 Maths Chapter 3 Examples 7:
Solve the following pair of equations by cross multiplication method.
2x + 3y = 46 …(1)
and 3x + 5y = 74 …(2)
To solve the equations by the cross-multiplication method, RHS must be zero.
2x + 3y – 46 = 0
3x + 5y – 74 = 0
Equation Reducible to Linear Equation in Two Variables
There are several situations which can be mathematically represented by two equations that are not linear to start with. But we alter them so that they are reduced to a pair of linear equations.
Class 10 Maths Chapter 3 Examples 8:
Solve the pair of equations: 2/x + 3/y = 13 and 5/x – 4/y = -2.
Given that
Let 1/x = p and 1/y = q. Then,
2p + 3q = 13 …(3)
and 5p – 4q = – 2 …(4)
Solving these two equations, we get p = 2, q = 3.
Thus, x = 1/p = 1/2 and y = 1/q = 1/3
Click below to get CBSE Class 10 Maths Chapter wise Revision Notes PDF.