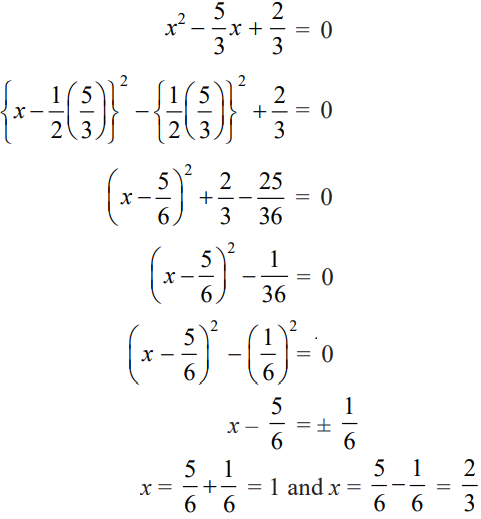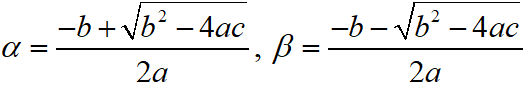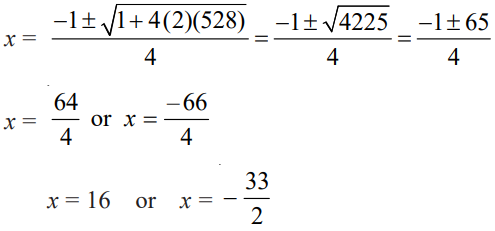Hi students, Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get Quadratic Equations CBSE Notes Class 10 Maths Chapter 4 PDF. You can download this PDF and save it in your mobile device or laptop etc. 

Quadratic Equations CBSE Notes Class 10 Maths Chapter 4

Quadratic Equations

The standard form of a quadratic polynomial is p(x) = ax² + bx + c. Then, ax² + bx + c = 0 is the general equation of quadratic equations, where a, b and c are real and a 0.

Since the degree of a quadratic equation is two, then the quadratic equation is satisfied by exactly two roots which may be real of imaginary.

Class 10 Maths Chapter 4 Examples 1: 

Check whether the equation x³ – 4x² – x + 1 = (x – 2)³ is quadratic or not.

x³ – 4x² – x + 1 = (x – 2)³

⇒ x³ – 4x² – x + 1 = x³ – 8 – 6x² + 12x

⇒ – 4x² – x + 1 = – 8 – 6x² + 12x

⇒ 2x² – 13x + 9 = 0

It is of the form ax² + bx + c = 0. So, the given equation is a quadratic equation. 

Solution of Quadratic Equations : By Factorization

A real number x = α is a root of the quadratic equation ax² + bx + c = 0, a ≠ 0 if α satisfies the quadratic equation it means, a α² + bα + c = 0.

Class 10 Maths Chapter 4 Examples 2: 

Find the roots of the following quadratic equations by factorization: x² – 3x – 10 = 0.

x² – 3x – 10 = 0

⇒ x² – 5x + 2x – 10 = 0

⇒ x(x – 5) + 2(x – 5) = 0

⇒ (x + 2)(x – 5) = 0

⇒ x = -2 or 5

Solution of Quadratic Equations : By Method of Completing Square

Class 10 Maths Chapter 4 Examples 2: 

Find the roots of the following quadratic equations by method of completing the square: 3x² – 5x + 2 = 0.

Given that 3x² – 5x + 2 = 0

Solution of Quadratic Equations : By Quadratic Formula

The roots of the quadratic equation ax² + bx + c = 0 are

Thus, the sum of the roots is α + β = -b/a and the product of the roots is αβ = c/a.

Class 10 Maths Chapter 4 Examples 3: 

Solve the quadratic equation 2x² + x – 528 = 0 by using quadratic formula.

Given that a = 2, b = 1 and c = -528

Nature of Roots of Quadratic Equations

In a quadratic equation ax² + bx + c = 0, the value D = b² – 4ac is known as discriminant of the quadratic equation.

The nature of the roots of the quadratic equation depends on the discriminant.

Case I: When D > 0

In this case, the roots α and β of the quadratic equation are real and unequal.

Case II: When D = 0

In this case, the roots α and β of the quadratic equation are real and equal.

Case III: When D < 0

In this case, the roots α and β of the quadratic equation are imaginary and distinct.

Class 10 Maths Chapter 4 Examples 4: 

Find the nature of the roots of the quadratic equation 2x² – 4x + 3 = 0.

Given that a = 2, b = -4 and c = 3.

Since the discriminant b² – 4ac = (– 4)² – (4 × 2 × 3) = 16 – 24 = – 8 < 0

Thus, So, the given equation has no real roots.

Class 10 Maths Chapter 4 Examples 5: 

Find the values of k for each of the quadratic equation 2x² + kx + 3 = 0, so that they have two
equal roots.

Given that a = 2, b = k and c = 3.

Since the given equation has equal roots, then

D = b² – 4ac = 0

⇒ k² – (4 × 2 × 3) = 0

⇒ k² = 24

⇒ k = 2√3.

Click below to get CBSE Class 10 Maths Chapter wise Revision Notes PDF.