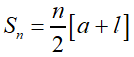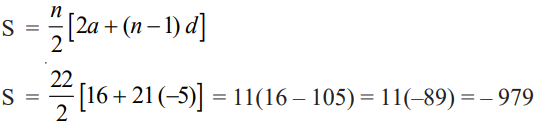Hi students, Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get Arithmetic Progressions CBSE Notes Class 10 Maths Chapter 5 PDF. You can download this PDF and save it in your mobile device or laptop etc. 

Arithmetic Progressions CBSE Notes Class 10 Maths Chapter 5 PDF

Arithmetic Progression

An arithmetic progression is a list of numbers in which each term is obtained by adding a fixed number to the preceding term except the first term. This fixed number is called the common difference of the AP and the common difference of AP can be positive, negative or zero. 

If the sequence t₁, t₂, t₃, …, t_n-1, t_n are in AP, then t₂ – t₁ = t₃ – t₂ = t₄ – t₃ = … = t_n – t_n-1 = d (common difference).

The sequence a, a + d, a + 2d, a + 3d, . . . represents an arithmetic progression where a is the first term and d the common difference. This is called the general form of an AP.

Class 10 Maths Chapter 5 Examples 1: 

Write first four terms of the AP, when the first term a = 10 and the common difference d = 10.

The arithmetic progression is

a, a + d, a + 2d, a + 3d, . . . ⇒ 10, 20, 30, 40, …

Class 10 Maths Chapter 5 Examples 2: 

Check whether the sequence 2, 4, 8, 16, . . . is in AP or not.

4 – 2 ≠ 8 – 4. Thus, the given sequence is NOT in AP.

Class 10 Maths Chapter 5 Examples 3: 

For the AP, 0.6, 1.7, 2.8, 3.9, . . ., write the first term and the common difference.

The first term of the AP is a = 0.6 and the common difference is d = 1.7 – 0.6 = 1.1.

n^th Term of General Term of an AP

If the sequence t₁, t₂, t₃, …, t_n-1, t_n are in AP, then the general term of the AP is t_n = a + (n – 1)d, where a is the first term (a = t₁) and d is the common difference (d = t₂ – t₁ = t₃ – t₂ = … etc). 

n^th Term of General Term of an AP from Last

Let a be the first term (a = t₁) and d be the common difference (d = t₂ – t₁ = t₃ – t₂ = … etc) of an AP having total N terms. Then, the n^th term from the end or last of the AP is the (N – n + 1)^th term from the beginning of the AP. 

Class 10 Maths Chapter 5 Examples 4: 

Find the 10th term of the AP : 2, 7, 12, . . .

Given that a = 2, d = 7 – 2 = 5.

Since t_n = a + (n – 1)d

⇒ t₁₀ = 2 + (10 – 1)(5) = 2 + 9 × 5 = 2 + 45 = 47

Class 10 Maths Chapter 5 Examples 5: 

Check whether 301 is a term of the list of numbers 5, 11, 17, 23, . . .

t_n = a + (n – 1)d

⇒ 301 = 5 + (n – 1)6

⇒ 301 = 5 + 6n – 6

⇒ 301 = 6n – 1

⇒ 6n = 302

⇒ n = 151/3 (Not Natural number).

Thus, 301 is not a term of the given sequence.

Class 10 Maths Chapter 5 Examples 6: 

Which term of the AP : 21, 18, 15, . . . is – 81?

Given that a = 21, d = 18 – 21 = -3.

Since t_n = a + (n – 1)d

⇒ –81 = 21 + (n – 1)(-3)

⇒ –81 = 21 – 3n + 3

⇒ 3n = 24 + 81 = 105

⇒ 3n = 105

⇒ n = 105 / 3 = 35

Sum of n Terms of an AP

Let a be the first term (a = t₁) and d be the common difference (d = t₂ – t₁ = t₃ – t₂ = … etc) of an AP having total n terms. Then, the sum of n terms of AP is 

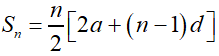
If the last term or n^th term of the AP is known, then the sum of n terms of AP is 

The sum of first n natural numbers is S = 1 + 2 + 3 + … + n = n(n + 1)/2.

Class 10 Maths Chapter 5 Examples 7: 

Find the sum of the first 22 terms of the AP : 8, 3, –2, . . ..

Given that a = 8, d = 3 – 8 = –5, n = 22.

Class 10 Maths Chapter 5 Examples 8: 

Find the sum of the first 1000 positive integers.

Required sum S = 1 + 2 + 3 + … + 1000 = 1000(1000 + 1)/2 = 500 × 1001 = 500500. 

Click below to get CBSE Class 10 Maths Chapter wise Revision Notes PDF.