Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Practice Test 30 Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Math Practice Test 30 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
Marty is planning which crops to plant on his farm for the upcoming season. He has enough seed to plant 4 acres of wheat and 7 acres of soybeans, but the total area of farmland he owns is only 9 acres. He earns $90 per acre for every acre of wheat planted and $120 for every acre of soybeans planted, and he must pay a 10% tax on all money he earns from selling his crops. What is the maximum profit, in dollars, that Marty can earn from planting wheat and soybeans this season?
Show/Hide Answer Key
Correct Answer: 918
To find the maximum profit, maximize the number of acres of soybeans Marty plants since soybeans bring in more money per acre than does wheat. At most, Marty can plant 7 acres of soybeans. Therefore, the most money he can make on soybeans is 7 × 120 = 840. He then has 9 – 7 = 2 acres left on which to plant wheat. The money he makes from this wheat is 2 × 90 = 180. The total amount Marty makes before taxes is therefore 840 + 180 = 1,020. The tax on this money equals 1,020 × 0.10 = 102. Subtract the amount Marty pays in taxes to get 1,020 – 102 = 918 profit. The correct answer is 918.
SAT Math Practice Online Test Question No 2:
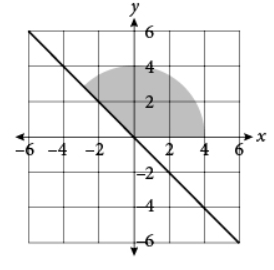
What are the area of the shaded region of the circle, bound by the x-axis and the line y = – x, rounded to the nearest whole number?
Show/Hide Answer Key
Correct Answer: 19
The formula for the area of a circle is A = πr2. If a full circle was shown, its radius would be 4, so the area of the full circle would be A = π42 = 16π. The interior angle of the fraction of the circle shown can be calculated as 90 + 45 = 135 degrees. Therefore, the figure shown is 135/360 of the area of a full circle. The area of the figure can be calculated as 135/360 (16π) = 0.375(16π) = 6π ≈ 18.8 ≈ 19. The correct answer is 19.
SAT Math Practice Online Test Question No 3:
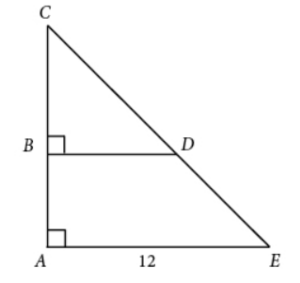
In the figure, AC is bisected by BD. If BC is 7, then what is the length of BD?
Show/Hide Answer Key
Correct Answer: 6
The two triangles share three angles, thus they are similar. AC is twice the length of BC because it is bisected by BD. This relationship is constant between the two similar triangles. Therefore, BD is half of AE: 12 ÷ 2 = 6.
SAT Math Practice Online Test Question No 4:
The daily recommended serving of protein is 50 grams. A nutritional bar contains 32% of the daily recommended serving of protein and 10% of the daily recommended serving of fat. If the nutritional bar contains 700% more grams of protein than grams of fat, what is the daily recommended serving of fat, in grams? (Disregard units when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 20
First, determine the grams of protein in the bar. If the bar contains 32% of the daily recommended serving of protein, and the daily recommended serving of protein is 50 grams, then the bar contains 0.32× 50 = 16 grams of protein. Next, determine the grams of fat in the bar by using the percent change equation: percent change = difference/original x 100.
The percent change is 700, and the original is the grams of fat (because percent more means the original is the smaller number), which means 700 = (16 – x)/x x 100.
Divide both sides by 100: 7 = (16 – x)/x.
Multiply both sides by x to get 7 x = 16 – x . Add x to both sides to get 8 x = 16. Divide both sides by 8 and you find x = 2. That is the number of grams of fat in the bar. To find the daily recommended serving of fat, translate English to math. 2 is 10% of the daily recommended serving, so if the daily recommended serving is y, 2 = 0.10y. Divide both sides by 0.10, and you find that the daily recommended serving of fat is 20.
SAT Math Practice Online Test Question No 5:
Set R consists of all the one-digit prime numbers. Set S contains all of the elements of Set R, as well as an additional positive integer, x.
If the sum of all of the elements of Set S is 30, what is the value of x2 – 11x – 25?
Show/Hide Answer Key
Correct Answer: 1
First, you need to determine the content of Set R . If Set R consists of all the one-digit prime numbers, then R = {2, 3, 5, 7}. The sum of the elements of Set S would therefore be 2 + 3 + 5 + 7 + x = 30. Combine like terms: 17 + x = 30. Subtract 17 from both sides, and you find x = 13. Plug x = 13 into the equation and solve: (13) 2 – 11(13) – 25 = 1.
SAT Math Practice Online Test Question No 6:
Set R consists of all the one-digit prime numbers. Set S contains all of the elements of Set R, as well as an additional positive integer, x.
Michael wants to change the value of x so that the mean of Set S is equal to the median of Set S and for Set S to have no mode. What value of x would accomplish his goal?
Show/Hide Answer Key
Correct Answer: 8
The additional positive integer x cannot equal 2, 3, 5, or 7 (otherwise there would be a mode). Next, determine what the median could be for various ranges of x. If x is less than 2, then the set would be, in consecutive order, { x, 2, 3, 5, 7}, making the median 3. Try this set. If the median equals the mean, then the sum of the elements divided by 5 (the number of elements) must equal 3: (x + 2 + 3 + 5 + 7)/5 = 3.
Multiply both sides by 5 and combine like terms: x + 17 = 15. Subtract 17 from both sides, and you find x = −2. However, x must be a positive integer, so this doesn’t work. Try a new median. If x = 4, then the set is {2, 3, 4 ( x ), 5, 7), with a median of 4. However, the mean is (2 + 3 + 4 + 5 + 7)/5 = 5.25, not 4, so this doesn’t work. If x is 6 or greater, the set would either be {2, 3, 5, 6 ( x ), 7} or {2, 3, 5, 7, x }. In either case, the median is 5. Set up the average equal to the median of 5: (2 + 3 + 5 + 7 + x)/5 = 5. Multiply both sides by 5 and combine like terms: 17 + x = 25. Subtract 17 from both sides, and you find that x = 8.
SAT Math Practice Online Test Question No 7:
Dan orders a soccer jersey online. If the jersey costs 40 euros and one euro is worth 1.2 dollars, how many dollars did Dan pay for the jersey?
Show/Hide Answer Key
Correct Answer: 48
Set up a proportion: 1 euro/1.2 dollars = 40 euros/x dollars. Cross-multiply and get x = 1.2 × 40 = 48.
SAT Math Practice Online Test Question No 8:
An ice cream cart vendor sells 50 popsicles on an average fall day. During the summer, the ice cream cart vendor sells 7 less than twice as many popsicles per day as he does on the average fall day. How many popsicles does the ice cream cart vendor sell in 6 summer days?
Show/Hide Answer Key
Correct Answer: 558
During the summer the ice cream vendor sells an average of 2(50) – 7 = 93 popsicles per day. Over 6 summer days, 93 × 6 = 558 popsicles are sold. The correct answer is 558.
SAT Math Practice Online Test Question No 9:
1.3g + 1.7h = 5
3h = 20 + 13g
Based on the system of equations above, what is the value of h?
Show/Hide Answer Key
Correct Answer: 3.5
Get rid of the decimals in the first equation by multiplying the first equation by 10 to get 13 g + 17 h = 50. In the second equation, move all the variables to the left of the equal sign to get -13 g + 3 h = 20. Whenever there are two equations with the same two variables, they can be solved simultaneously by adding or subtracting them. The key is to get one variable to cancel out. Stack the equations on top of each other and add them.
13g + 17h = 50
-13g + 3h = 20
20h = 70
Therefore, h = 70/20. Because this number is too large to grid in, either reduce the fraction to 7/2 or convert the fraction to the decimal 3.5.
SAT Math Practice Online Test Question No 10:
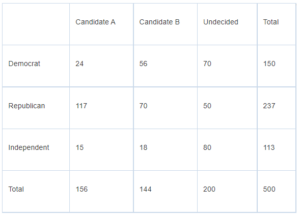
The table above illustrates the results of a political poll. Five hundred voters were first asked whether they were registered as Democrat, Republican, or Independent. The voters were then asked whether they planned to vote for Candidate A, for Candidate B, or were Undecided. What percent of the registered Democrats plan to vote for Candidate A? (Disregard the percent symbol when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 16
To find the percent of registered democrats planning to vote for candidate A, divide the number of Democrats planning to vote for candidate A by the total number of registered democrats: 24/150 = 0.16 = 16%, which makes 16 the correct answer.