Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Questions Test 31 Grid Ins Problems with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Math Questions Test 31 Grid Ins Problems with Answer Keys
SAT Math Practice Online Test Question No 1:
x ≥ 0
3y – 2x ≥ -12
2x + 5y ≤ 20
What is the area of the triangle formed in the xy -plane by the system of inequalities above?
Show/Hide Answer Key
Correct Answer: 30
Start by drawing the picture, as this question doesn’t provide one. To do so, change each of the equations into the slope-intercept form of an equation y = mx + b, where m is the slope and b is the y-intercept. The second equation becomes 3 y ≥ 2 x – 12, or y ≥ (2/3)x – 4. The third equation becomes 5 y ≤ -2 x + 20, or y ≤ (-2/5)x + 4. The ≥ sign in the second equation means that everything above the line should be shaded, and the ≤ sign in the third equation means that everything below that line should be shaded. To graph the first equation x ≥ 0, shade everything to the right of the y -axis. The resulting figure should look like this.
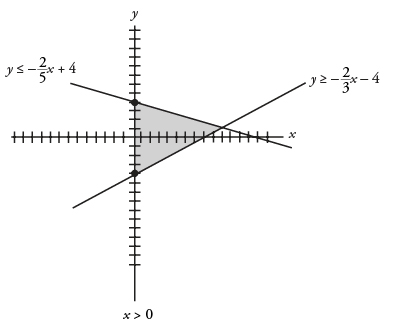
The formula for the area of a triangle is A = (1/2)b x h. It is easiest to think of the side that is along the y -axis as the base. That side goes from a y -coordinate of 4 to -4, for a length of 8. The height of the triangle is the x -coordinate of the point where the two slanted lines meet; set the two equations equal to find it. Start with (2/3)x – 4 = (-2/5)x + 4. and multiply everything by 15 to get 10 x – 60 = – 6 x + 60. Then add 6 x and 60 to both sides to get 16 x = 120, so x = 7.5, and the height is 7.5. The resulting figure should look like this.
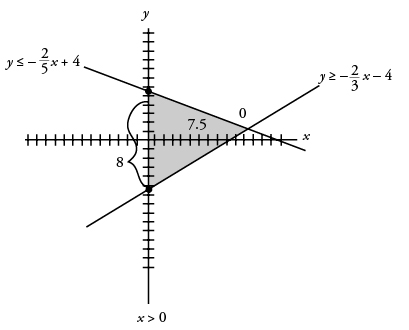
Plug the measurements for the base and the height into the area formula to get A = (1/2)(8)(7.5) = 30. The correct answer is 30.
SAT Math Practice Online Test Question No 2:
The Nile is a track and field athlete at North Sherahan High School. He hopes to qualify for the Olympic Games in his best field event, the javelin throw. He experiments with different javelin weights to build his arm strength and currently measures the results in feet.
The distance at which the Nile can throw a javelin is inversely proportional to the weight of that javelin. The Nile can throw a 1.5-pound javelin exactly 260 feet. How far would the Nile be able to throw a 2-pound javelin, in feet, assuming all other factors remain constant? (Disregard units when inputting your answer.)
Show/Hide Answer Key
Correct Answer: 195
Use the definition of inverse proportion: x1 y1 = x2 y2 . Plug in 1.5 for x1 , 260 for y1 , 2 for x2 , and solve for y2 : (1.5)(260) = (2)( y2 ); 390 = 2 y2 . Divide both sides by 2, and you find y2 = 195.
SAT Math Practice Online Test Question No 3:
At a certain restaurant, milkshakes cost $4 and cheeseburgers cost $6. If Al buys 1 milkshake and x cheeseburgers and spends at least $30 but no more than $46, what is one value of x?
Show/Hide Answer Key
Correct Answer: 5, 6 or 7
Work Bite-Sized Pieces and translate English to math.
If Al buys 1 milkshake and x cheeseburgers, then he spends 1 times the cost of a milkshake ($4) and x times the cost of a cheeseburger ($6), which translates to 4 + 6 x. This must be at least $30; “at least” translates to ≥ in math, so 4 + 6 x ≥ 30.
Subtract 4 from both sides to get 6 x ≥ 26. Divide both sides by 6 to get x ≥ 4.3. You can’t order a fractional number of cheeseburgers, so try 5 cheeseburgers. This would give a total of 4 + 6(5) = $34, which satisfies the question.
Input 5 as your answer. 6 and 7 are also acceptable answers, as those numbers of cheeseburgers will be $40 and $46, respectively.
SAT Math Practice Online Test Question No 4:
Age of the first fourteen Indian Prime Ministers upon taking office
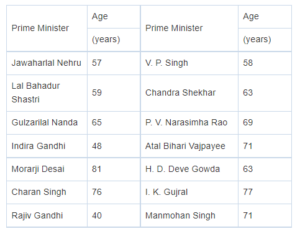
The table above shows the ages of the first 14 Indian prime ministers when they began terms in office. According to the table, what is the mean age, in years, of these prime ministers at the beginning of their terms? (Round your answer to the nearest tenth.)
Show/Hide Answer Key
Correct Answer: 64.1
To find the mean, find the sum of all the ages and divide by the number of people:
[57 + 59 + 65 + 48 + 81 + 76 + 40 + 58 + 63 + 69 + 71 + 63 + 77 + 71]/14 = 898/14 = 64.1
SAT Math Practice Online Test Question No 5:

A state highway department uses a salt storage enclosure that is in the shape of a cone, as shown above. If the volume of the storage enclosure is 48 π m 3, then what is the diameter of the base of the cone, in meters?
Show/Hide Answer Key
Correct Answer: 8
Use the Geometry Basic Approach.
First, write down the formula you need: the volume of a cone, which is V = (1/3)πr2 h. Plug-in what you know: 48π = (1/3)πr2(9).
Solve for r; start by combining like terms on the right: 48π = 3 πr2. Divide both sides by 3π : 16 = r2 . Take the square root of both sides, and you find r = 4.
Be careful! The question is asking for diameter, so double the radius to find the diameter is 8.
SAT Math Practice Online Test Question No 6:
Marginal cost is the increase or decrease in the total cost a business will incur by producing one more unit of a product or serving one more customer. Marginal cost can be calculated using the equation M = C₂ – C₁/Q₂ – Q₁, where M is the marginal cost, C1 is the total cost for Q1 units, and C2 is the total cost for Q2 units.
At Carol’s Steakhouse, the total cost of serving 150 customers per day is $900. Carol is interested in increasing her business but is concerned about the effect on marginal cost.
Carol calculates that the total cost of serving 200 customers per day would be $1,600. What is the marginal cost of this increase in customers?
Show/Hide Answer Key
Correct Answer: 14
Use the formula provided and the information is given.
If it costs $900 for 150 customers, then C1 = 900 and Q1 = 150. Similarly, if it would cost $1,600 for 200 customers, then C2 = 1,600 and Q2 = 200. Plug these values into the equation and solve: M = 1,600 – 900/200 – 150 = 700/50 = 14.
SAT Math Practice Online Test Question No 7:
A climate change panel estimates that New York City’s sea levels are rising at a rate of 1.2 inches every 10 years. According to the panel’s estimate, how long will it take, in years, for New York City’s sea levels to rise by 14.4 inches?
Show/Hide Answer Key
Correct Answer: 120
Set up a proportion: 1.2 inches/10 years = 14.4 inches/x years.
Cross-multiply to get 1.2 x = 144. Divide both sides by 1.2 and you get x = 120.
SAT Math Practice Online Test Question No 8:
A regional radio station sells time slots for advertisements in 30-second intervals. If the station airs advertisements for 220 minutes per day, every day of the week, what is the total number of 30-second advertisement time slots the station can sell for Thursday and Friday?
Show/Hide Answer Key
Correct Answer: 880
Over two days, the radio station airs a total of 220 × 2 = 440 minutes of advertisements. If each time slot is 30 seconds long, and each minute has 60 seconds, then there is time for 60 ÷ 30 = 2-time slots per minute, giving a total of 440 × 2 = 880-time slots over two days.
SAT Math Practice Online Test Question No 9:
c = 800t + 950
Swathi made an initial contribution to a Roth IRA retirement account. Each year thereafter she contributed a fixed amount to the account. The equation above models the amount c, in dollars, that Swathi has contributed after t yearly contributions. According to the model, how many dollars was Swathi’s initial contribution? (Disregard the $ sign when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 950
The initial contribution will be before any yearly contributions, so t = 0. If t = 0, then c = 800(0) + 950 = $950. Swathi’s initial contribution must therefore be $950.
SAT Math Practice Online Test Question No 10:
Mali is a landlocked country in western Africa. In 2015, its population was estimated to be 14.5 million. For the following 10 years, the population of Mali was projected to grow by 3 percent each year; this relationship can be modeled by the equation P = 14.5(r)y, where P is the population, in millions, y years after 2015.
What is the value of r in the equation above?
Show/Hide Answer Key
Correct Answer: 1.03
The given equation is the equation for exponential growth. The generic form of this equation is final amount = original amount (1 ± rate ) number of changes.
The rate of growth is 3 percent, which as a decimal is equal to 0.03. Because the question indicates that the population is growing, you need to add this to 1, so the value in the parenthesis, r, is 1 + 0.03 = 1.03.



