Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Practice Online Test 32 Grid Ins Questions with Answer Keys | SAT Online Classes AMBiPi.
SAT 2022 Math Practice Online Test 32 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
When (x2 + 2x – 3)(2x + 5) – (x + 1)(x – 1)(x + 3) is expressed in the form ax3 + bx2 + cx + d, what is the value of a + b + c + d ?
Show/Hide Answer Key
Correct Answer: 0
Start by multiplying the terms together. To multiply (x2 + 2 x – 3)(2 x + 5), multiply each term in the left parenthesis by each term in the right parenthesis to get 2x3 + 5x2 + 4x2 + 10x – 6x – 15.
Combine like terms to get 2x3 + 9x2 + 4x – 15. To multiply (x + 1)(x – 1)(x + 3), multiply only two sets of parentheses first, then multiply that product by the remaining parenthesis. You may notice that (x + 1)( x – 1) is a common quadratic, which equals x2 – 1. Then, multiply x2 – 1 by (x + 3).
As you did before, multiply each term in the first parenthesis by each term in the second to get x3 + 3x2 – x – 3. Now, you can calculate (2x3 + 9x2 + 4x – 15) – (x3 + 3x2 – x – 3).
You can distribute the negative sign into the second parenthesis: (2x3 + 9x2 + 4x – 15) + (- x3 – 3x2 + x + 3). Now you can combine like terms to get x3 + 6x2 + 5x – 12. This is in the form ax3 + bx2 + cx + d , so a = 1, b = 6, c = 5, and d = -12. This means a + b + c + d = 1 + 6 + 5 + (-12) = 0.
SAT Math Practice Online Test Question No 2:
The Nile is a track and field athlete at North Sherahan High School. He hopes to qualify for the Olympic Games in his best field event, the javelin throw. He experiments with different javelin weights to build his arm strength and currently measures the results in feet.
During his preparations, Nile realizes that the upcoming Olympic qualifying competition will be judged in meters, rather than feet or yards. The Nile wants to make sure he can throw the javelin the minimum required distance so he can advance in the competition. If his current best throw is 60 yards, and one yard is approximately 0.9144 meters, how much further, to the nearest yard, must he throw to achieve the minimum required distance of 68.58 meters to qualify for the Olympics? (Disregard units when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 15
Start by converting the qualifying distance of 68.58 meters into yards.
Set up a proportion of 1 yard/0.9144 meters = x yards/68.58 meters. Cross-multiply to get 0.9144 x = 68.58. Divide both sides by 0.9144 to find that the qualifying distance is 75 yards. If Nile’s current throw is 60 yards, he needs to throw 75 – 60 = 15 more yards.
SAT Math Practice Online Test Question No 3:
A bowl with 300 milliliters of water is placed under a hole where the rain gets in. If water drips into the bowl at a rate of 7 milliliters per minute, then how many milliliters of water will be in the bowl after 50 minutes?
Show/Hide Answer Key
Correct Answer: 650
Break the problem into Bite-Sized Pieces. First, determine how much water is added in 50 minutes. Rate = Amount/Time, so Rate × Time = Amount. 7 × 50 = 350 milliliters added over 50 minutes. Add this to the original 300 milliliters: 350 + 300 = 650.
SAT Math Practice Online Test Question No 4:
In one month, Rama and Siham ran for a total of 670 minutes. If Rama spent 60 fewer minutes running than Siham did, for how many minutes did Siham run?
Show/Hide Answer Key
Correct Answer: 365
To solve for Siham, translate from English to math and solve the system of equations.
Make the number of minutes Rama ran r and the number of minutes Siham ran s. If Rama and Siham ran for a total of 670 minutes, then the number of minutes Rama ran plus the number of minutes Siham ran equals 670, or r + s = 670.
For the second equation, Rama’s total amount of time was 60 minutes less than Sihams, so r = s – 60. Because you want to solve for s, you can substitute s – 60 for r in the first equation: (s – 60) + s = 670.
Combine like terms: 2 s – 60 = 670. Add 60 to both sides: 2 s = 730. Divide both sides by 2, and you get s = 365.
SAT Math Practice Online Test Question No 5:
Which f(x) = 1/[(x – 12)2 + 14(x – 12) + 49]
For what value of x is the function f above undefined?
Show/Hide Answer Key
Correct Answer: 5
For this function to be undefined, the denominator must be equal to 0. So, set the denominator equal to 0 and solve: (x – 12)2 + 14(x – 12) + 49 = 0 .
Start by FOILing the first parenthesis and distributing 14 in the second: x2 – 24x + 144 + 14x – 168 + 49 = 0 .
Combine like terms: x2 – 10x + 25 = 0. You might recognize this as a perfect square; it factors to (x – 5)(x – 5) = 0. Therefore, the value of x that makes function f undefined is 5.
SAT Math Practice Online Test Question No 6:
Marginal cost is the increase or decrease in the total cost a business will incur by producing one more unit of a product or serving one more customer. Marginal cost can be calculated using the equation M = C₂ – C₁/Q₂ – Q₁, where M is the marginal cost, C1 is the total cost for Q1 units, and C2 is the total cost for Q2 units.
At Carol’s Steakhouse, the total cost of serving 150 customers per day is $900. Carol is interested in increasing her business but is concerned about the effect on marginal cost.
Carol successfully increases her business to 200 customers per day. However, her total cost for doing so is 50% greater than the expected $1,600. What percent greater is the actual marginal cost than the expected marginal cost, to the nearest full percent? (Note: Ignore the percent sign when entering your answer. For example, if your answer is 326%, enter 326.)
Show/Hide Answer Key
Correct Answer: 114
Take this in Bite-Sized Pieces. If the actual cost is 50% greater than expected, and Carol expected the cost to be $1,600 (as question 37 tells us), then the actual cost was 1,600 + 0.50(1,600) = $2,400. This is the new value of C2 . Plug this value into the equation, using the same values as before for C1 , Q2 , and Q1 : M = 2,400 – 900/200 – 150 = 30.
To find the percent increase in marginal cost, use the equation percent change = difference/original x 100. So the percent change is (30 – 14)/14 x 100 = 114%.
SAT Math Practice Online Test Question No 7:
In the xy -plane, the point (2, 10) lies on the graph of the function f (x) = 2x2 + bx – 8. What is the value of b?
Show/Hide Answer Key
Correct Answer: 5
Because the point (2, 10) lies on the graph, you can make x = 2 and f (x) = 10 and solve for b : 10 = 2(2)2 + b (2) – 8; 10 = 8 + 2 b – 8; 10 = 2 b ; b = 5.
SAT Math Practice Online Test Question No 8:
A local frozen yogurt store views percentage rates of how many total viewers clicked on posts on its social media page. On the first 8 posts the store posted, the average (arithmetic mean) of the clicked-on percentage rates was 60%. What is the least value the page can receive for the 9th rating and still be able to have an average of at least 75% for the first 16 posts? (Disregard the % sign when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 20
Average is total/number of things, which can be rearranged as average × number of things = total . If the desired average for 16 posts is 75%, then the sum of all the scores must be 75 × 16 = 1,200%.
For the first 8 posts, there was a total of 60 × 8 = 480%, leaving 1,200 – 480 = 720% for the last 8 posts. If you want the least value for the 9th post, then you want to assume that the 10th-16th posts to be as high as possible, or 100%.
This would give 100 × 7 = 700% total for the last 7 posts, making the least value possible for the 9th post 720 – 700 = 20%.
SAT Math Practice Online Test Question No 9:
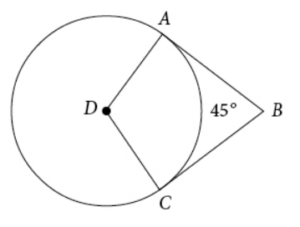
In the figure above, point D is the center of the circle, line segments AB and BC are tangent to the circle at points A and C, respectively, and the segments intersect at point B as shown. If the circumference of the circle is 64, what is the length of major arc AC ?
Show/Hide Answer Key
Correct Answer: 40
Arc is proportionate to the central angle: central angle/360° = arc/circumference.
For a major arc, you need to use the central angle measure that’s greater than 180° (the central angle measure that’s less than 180° is the minor arc). Therefore, here you need to find angle ADC (the angle from the minor arc) and subtract that from 360° to get the angle for the major arc.
To get angle ADC, consider quadrilateral ABCD. A quadrilateral has 360°. Because AB and CB are tangents to the circle, angles DAB and DCB are each 90°, leaving 360 – 90 – 90 – 45 = 135° for angle ADC. The angle you need to use to find the major arc is therefore 360 – 135 = 225°. Insert this into the proportion: 225°/360° = x/64, where x is the arc.
Cross-multiply to get 14,440 = 360 x. Divide both sides by 360 to get x = 40.
SAT Math Practice Online Test Question No 10:
Mali is a landlocked country in western Africa. In 2015, its population was estimated to be 14.5 million. For the following 10 years, the population of Mali was projected to grow by 3 percent each year; this relationship can be modeled by the equation P = 14.5(r)y , where P is the population, in millions, y years after 2015.
What is the projected population of Mali in 2022, in millions, to the nearest tenth of a million?
Show/Hide Answer Key
Correct Answer: 17.8
The year 2022 is 7 years after 2015, so y = 7. Put these into the equation to determine P : P = 14.5(1.03) 7 = 17.8.



