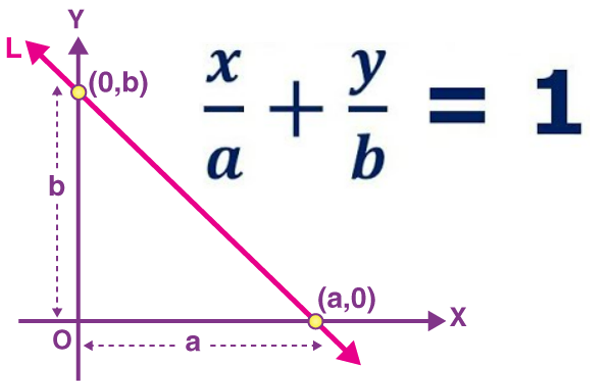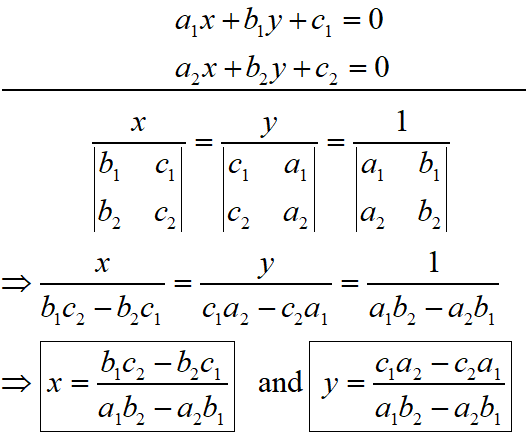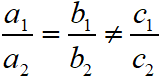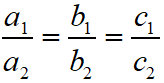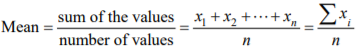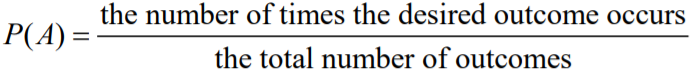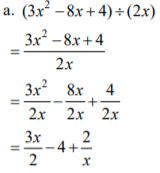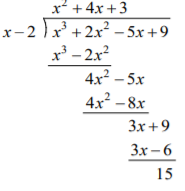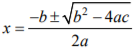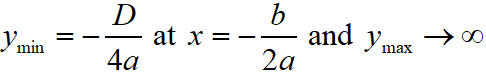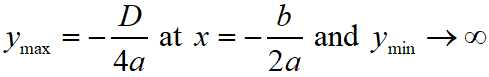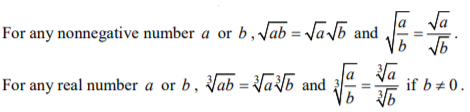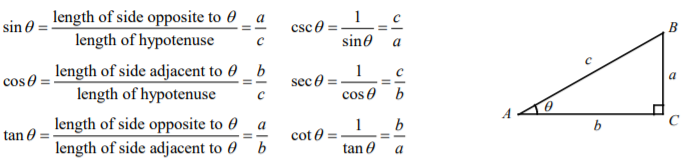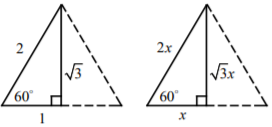Welcome to AMBiPi (Amans Maths Blogs).
Download this Article as PDF
NOTE : (Practice Questions are Given on Home Page of This Website.)
SAT 2023-24 Math Topics
In this article, you will get SAT Math Topics 2023-24 List PDF Download | SAT Math Online Crash Course AMBiPi. AMBiPi observes the pattern of SAT Math Section of SAT Past Papers from 2002 to 2021, there are following SAT Math Topics from where SAT Math Questions is asked in SAT Papers.
- Numerical Calculation
- Algebraic Problems in One Variables
- Solving Inequations
- Algebraic Word Problems
- Addition and Subtraction Methods
- Substitution Methods
- Transforming Equations with More than One Variables
- Parallel and Perpendicular Lines
- Equation of a Line
- Absolute Value Problems
- Graphing Inequalities
- Word Problems in Geometry
- Word Problems in Statistics
- Word Problems in Inequations
- Word Problems with Multi Variables
- Word Problems with Rational Expression
- Additional and Subtraction of Polynomials
- Multiplication of Polynomials
- Division of Polynomials
- Long Division of Polynomials
- Factoring Polynomials
- Factoring Quadratic Polynomials
- Special Products
- Equations with Radicals
- Simplifying Rational Expressions
- Conjugate and Rationalizing the Denominators
- Operations with Exponents
- Transformation of Graphs
- Transformation of Quadratic Functions
- Word Problems with Quadratic
- Volume of Solids
- Volume and Area
- Pythagorean Theorems and Special Right Triangles
- Congruent and Similar Triangle
- Triangles Theorems
- Tangent to Circles
- Arcs, Sectors and Central Angles
- Equation of Circles
- Sine Cosine of Complementary Angles
- Angles of Elevation and Depressions
- Simplifying Expression with Complex Numbers
- Bar Graphs and Pie Charts
- Analysis of Two Way Tables
- Measures of Central and Spread
- Scatter Plots
- Measures of Errors
- Independent and Dependent Events
- Time and Work Problems
- Ratios and Proportions and Percentage
- Mixture Problems
- Density
SAT 2023-24 Math Online Crash Course PDF
To master the above SAT Math Topics, you need a SAT Math Formulas Notes Reference Cheat Sheet Checklist. This SAT Math Formulas Reference Sheet PDF is equivalent to SAT Math Online Crash Course, which helps you to get 800 marks in SAT Math section.
In SAT exam, the math sections includes Heart of Algebra, Problem Solving and Data Analysis, Passport to Advance Math, Additional Topics in Math.
SAT Math Formula Sheet | Heart of Algebra
NOTE : (Practice Questions are Given on Home Page of This Website.)
In SAT Math Heart of Algebra, there are following SAT Math Topics are included. You need to read this SAT Math Formula Sheet carefully to become a master in Heart of Algebra topics of SAT Math. This SAT Math Algebra Formulas Notes is a last minute sat math formulas pdf.
- Number System
- Number Line
- Natural Numbers
- Whole Numbers
- Integers
- Positive Integers
- Negative Integers
- Consecutive numbers
- Consecutive Numbers Formula
- Rational Numbers
- Irrational Numbers
- Real Numbers
- Imaginary Numbers
- Complex Numbers
- Basic Algebra
- Variables
- Algebraic Expression
- PEDMAS or Order of Operations
- Simplifying Algebraic Expression
- Algebraic Identities
- Slope of Line
- Slope of Line
- Slope of Horizontal and Vertical Lines
- Parallel Lines
- Perpendicular Lines
- Equation of Line in Slope Intercept Form
- Equation of Line in Point Slope Form
- Equation of Line in Intercept Form
- Linear Equations
- Linear Equations
- Linear Equations in One Variables
- How To Solve Linear Equations in One Variables
- Linear Equations in Two Variables
- Solving System of Linear Equations in Two Variables
- Solving System of Linear Equations in Two Variables by Elimination Method
- Solving System of Linear Equations in Two Variables by Substitution Method
- Solving System of Linear Equations in Two Variables by Cross Multiplication Method
- Number of Solutions of System of Linear Equations in Two Variables
- Word Problems of System of Linear Equations in Two Variables
- Functions
- Linear Functions
- Value of Linear Functions
- Composition of Functions
- Average Rate of Change of Functions
- Average Rate of Change of Linear Functions
- Average Rate of Change of Non-Linear Functions
- Absolute Value of a Number
- Absolute Value Functions
- Inequalities
- What are Inequalities or Inequations?
- Intervals
- Properties of Inequality
- Solving Inequalities
- System of Linear Inequalities in One Variables
- System of Linear Inequalities in Two Variables
- Solving System of Linear Inequalities in Two Variables
- Absolute Value Inequalities
- Quadratic Inequalities
- Graphing System of Inequalities
Let’s learn these SAT math topics of Heart of Algebra, one by one.
Number System
In number system of SAT Algebra syllabus, you need to learn the concepts of number line, classification of numbers such as natural numbers, whole numbers, integers, rational and irrational numbers, real numbers etc.
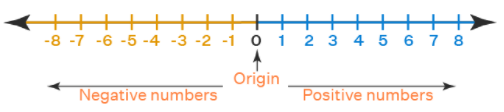
Number Line
A straight line on which the numbers are represented is called as Number Line. On this number line, there is a negative side, zero, and positive side.
All the numbers to the left of 0 are negative numbers and all the numbers to the right of 0 are all positive numbers.
Thus, you can say the numbers present on the right are larger than the numbers on their left.
Natural Numbers
Natural numbers are the counting numbers and it is right side of zero on number line.
Natural numbers are positive integer which starts from 1 to infinity.
The first 100 natural numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 and 100.
Whole Numbers
Whole numbers are the counting numbers and it is also right side of zero on number line.
Whole numbers are non-negative integer which starts from 0 to infinity.
All SAT Math Formulas : Integers
An integer is a number in which there is NO fractional or decimal part. The integers can be positive or negative. The set of integers includes positive integers, negative integers and zero.
The zero has no sign, it mean zero is neither positive nor negative.
Positive Integers
A positive integer is the numbers in the right side of zero on number line. The positive integers are also called as natural numbers.
Negative Integers
A negative integer is the numbers in the left side of zero on number line. The negative integers are negative of the natural numbers.
Consecutive Numbers
Consecutive numbers or integers is a group of numbers that follows a regular counting order or pattern where the difference between any two consecutive number is fixed.
For example: 1, 2, 3 are three consecutive numbers, 53,54, 55, 56, 57 are five consecutive numbers.
The number immediately before a number is called its predecessor. The number immediately after a number is called its successor.
Consecutive Numbers Formula
If n is the first number, then other consecutive numbers are (n + 1), (n + 2), (n + 3), … etc.
Even consecutive numbers formulas are 2n, (2n + 2), (2n + 4), (2n + 6), etc.
Even consecutive numbers formulas are (2n + 1), (2n + 3), (2n + 5), (2n + 7), etc.
Rational Numbers
A rational number that can be written in the form of p/q, where p and q are integers and q is not equal to 0.
For example: 1/2, -3/4 5/7 etc.
A fraction is a part of whole.
Therefore, a rational number can be positive or negative but a fraction is always positive.
In decimal expansion of rational number, a rational number is a terminating or non-terminating with recurring decimals numbers.
Irrational Numbers
An irrational number that is not a rational number. It means, an irrational number cannot be written in the form of ratio of integers.
For example: √2 and √3 etc. are irrational.
In decimal expansion of irrational number, an irrational number is a non-terminating or non-recurring decimals numbers.
Real Numbers
A real number is a set of rational and irrational numbers. All the numbers represented on number line are called real numbers.
For example: 3/5, -8/11, 12, -9, √2 and √3 etc. are real numbers.
Imaginary Numbers
An imaginary number is a number which is NOT a real number and hence it cannot be represented on number line.
The square of a real number is always positive whereas the square of an imaginary number is always negative.
The imaginary numbers are written as a real number multiplied with “i”, where “i” stands for IOTA and i = √(-1) or i2 = -1.
For example: 3i, -5i, (7/2)i etc.
Complex Numbers
A complex number is a combination of a real number and an imaginary number.
Hence, the complex number can be written in form of (a + bi), where “a” is a real part and “b” is an imaginary part.
For example: 1 + 3i, -5 + 8i, -3 – 6i etc.
Basic Algebra
In basic algebra of SAT Algebra syllabus, you need to learn the variables, constants, algebraic expression, order of operations, and algebraic identities.
Variables
A variable is an alphabet letter which represents an unknown value in algebra whose value can be found by performing algebraic operations.
For example: in the equation a + b = 5, a and b are variables.
When an equation includes a variable, which makes the equation is called solution to that equation.
Algebraic Expression
An algebraic expression is a mathematical statement in which variables, coefficient, constants and mathematical operators are there. For example: 12x + 5y + 9 is an algebraic expression in which 12 is coefficient of x, 5 is coefficient of y, 9 is a constant and “+” is a mathematical sign.
PEDMAS or Order of Operation
The PEDMAS is a concept that help us to simplify the math problems containing more than one mathematical operators. PEDMAS is an acronym whose full form is as below.
|
P → Parentheses ( ), { }, [ ]
|
|
E → Exponent or Index
|
|
D → Division (÷)
|
|
M → Multiplication (x)
|
|
A → Addition (+)
|
|
S → Subtraction (-)
|
For example: You need to simplify 2 – (12 x 3 + 5 – 6). What are the order of operations to be performed first; first we add or first we multiply or subtract? Hence, you need to use PEDMAS.
Simplifying Algebraic Expression
To simplify an algebraic expression, you need to combine the like terms. Like terms in algebraic expression are added or subtracted.
For example: 3x3 + 4x2 − 2x3 + 7x − x2 + 10 − 2x = (3x3 − 2x3) + (4x2 − x2) + (7x − 2x) + 10 = x3 + 3x2 + 5x + 10.
Algebraic Identities
To solve algebra questions, you need to learn algebraic identities. There are following algebraic identities.
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a + b)(a – b) = a2 – b2
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
- (a + b – c)2 = a2 + b2 + c2 + 2ab – 2bc – 2ca
- (a – b + c)2 = a2 + b2 + c2 – 2ab – 2bc + 2ca
- (a – b – c)2 = a2 + b2 + c2 – 2ab + 2bc – 2ca
- (- a + b + c)2 = a2 + b2 + c2 – 2ab + 2bc – 2ca
- (a + b)3 = a3 + b3 + 3ab(a + b)
- (a – b)3 = a3 – b3 – 3ab(a – b)
- a3 + b3 = (a + b)3 – 3ab(a + b) = (a + b)(a2 – ab + b2)
- a3 – b3 = (a – b)3 + 3ab(a – b) = (a – b)(a2 + ab + b2)
- a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
- If (a + b + c) = 0, then a3 + b3 + c3 = 3abc
Slope of Line
In slope of line of SAT Algebra syllabus, you need to learn finding the slope of a line, slopes of parallel lines and perpendicular lines, slope-intercept form of line, point slope of line, intercept form of line etc.
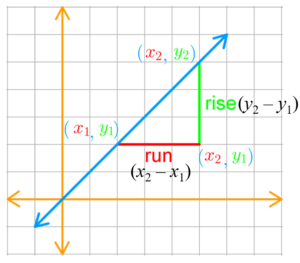
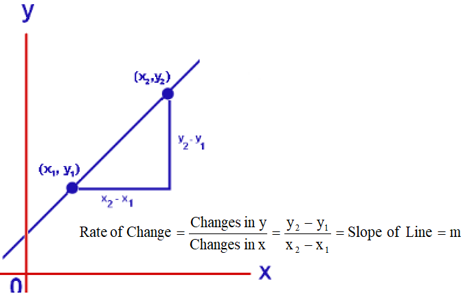
Slope of Line
The slope of a line that contains the point A(x1, y1) and B(x2, y2) is defined as
Slope (m) = Rise / Run = (Change in y) / (Change in x) = (y2 – y1) / (x2 – x1)
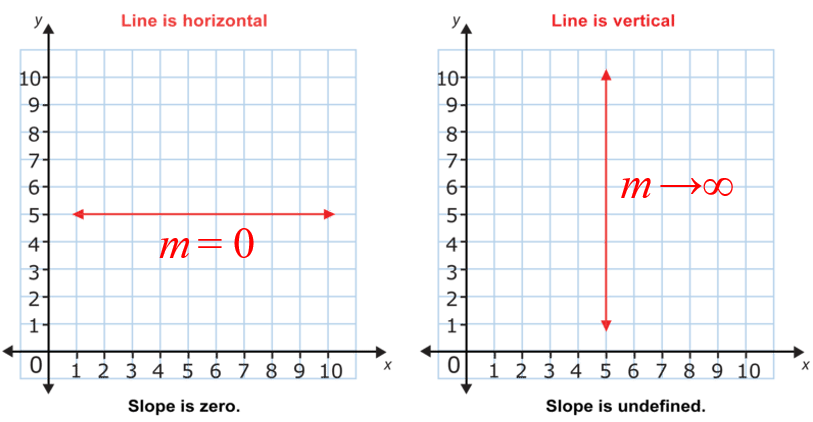
Slope of Horizontal and Vertical Line
When a line becomes horizontal, then the rise is zero, so the slope (m) = Rise / Run = 0. Hence, the slope of a horizontal line is zero.
When a line becomes vertical, then the run is zero, so the slope (m) = Rise / Run → ∞. Hence, the slope of a vertical line is infinity.
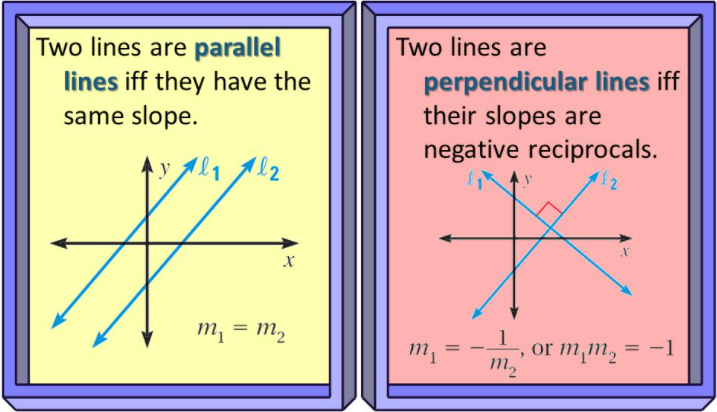
Parallel and Perpendicular Lines
If the line l1 has slope m1 and the line l2 has slope m2, then the lines l1 and l2 are parallel if m1 = m2.
If the line l1 has slope m1 and the line l2 has slope m2, then the lines l1 and l2 are perpendicular if m1m2 = -1.
Equation of a Line in Slope Intercept Form
If a line L makes an intercept length as b on y-axis with the slope m, then the line is in slope-intercept form and hence its equation is y = mx + b.
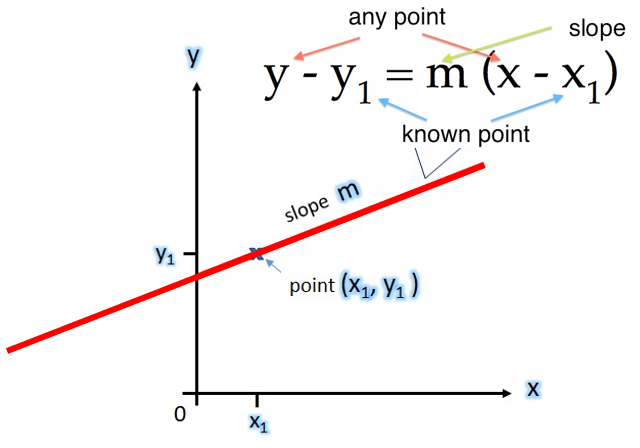
Equation of a Line in Point Slope Form
If a line L with the slope m and passes through the point (x1, y1), then the line is in point-slope form and hence its equation is y – y1 = m(x – x1).
Equation of a Line in Intercept Form
If a line L makes intercepts on both axes as a and b, then the equation of a line x/a + y/b = 1.
Equation of a Line in Standard Form
The standard form of equation of a line is ax + by + c = 0.
Linear Equations
In linear equation of SAT Algebra syllabus, you need to learn how to solve system of linear equations using elimination method, substitution method, cross multiplication method, graphical method and how to find number of solutions without solving the system of linear equations and word problems based on system of linear equations etc.
Linear Equations
An equation whose the degree of the variables is always 1 is known as linear equations. A linear equation is also called a one-degree equation.
Linear Equations in One Variable
A linear equation in which there is only one variable is known as linear equations in one variable. The standard form of linear equation in one variable is ax + b = 0, where x is a variable, a is coefficient of x and b is a constant term. For example: 3x + 6 = 0, -5x + 9 = 0 etc.
How to Solve Linear Equations in One Variable
To solve a linear equation in one variable, you need to perform the algebraic operation on both sides of the equation so that the variable is left on one side and all other terms in other side. Now, this value of x is the solution of the linear equation in one variable. Let’s understand with an example.
For example:
Solve 4x + 8 = 0.
Solution:
4x + 8 = 0
⇒ 4x = -8
⇒ x = -8/4
⇒ x = -2 is the solution of the given equations.
Linear Equations in Two Variables
A linear equation in which there are two variables is known as linear equations in two variables. The standard form of linear equation in two variable is ax + by + c = 0, where x and y are variables, a is coefficient of x, b is coefficient of y and c is a constant term.
For example: 3x + 6y + 11 = 0, -5x + 9y – 8 = 0 etc.
System of Linear Equations in Two Variables
A system of linear equations in two variables is of the form as below.
a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0
Solving System of Linear Equations in Two Variables
To solve the system of linear equations in two variables as a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0, there are three methods: elimination method, substitution method, cross multiplication method, graphical method.
Solving System of Linear Equations in Two Variables by Elimination Method
To solve the system of linear equations in two variables as a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 by elimination method, you need to equate the coefficients of any one variable and then eliminated by adding or subtracting the equations. After elimination, the final equation is of the form of linear equation in one variable which is very easy to solve by algebraic operations on both sides.
To understand the elimination method of solving system of linear equations, let’s solve the equations as below.
For example: Solve the system of equations as
Equation 1: 2x + 3y = 8
Equation 2: 3x + 2y = 7
From 2 × (Equation 1) – 3 × (Equation 2), you get
(4x + 6y) – (9x + 6y) = 16 – 21
⇒ -5x = -5
⇒ x = 1
Now, from Equation 1, you get
2(1) + 3y = 8
⇒ 3y = 8 – 2
⇒ 3y = 6
⇒ y = 6/3
⇒ y = 2
Hence, x = 1 and y = 2 are the solutions of given equation.
Solving System of Linear Equations in Two Variables by Substitutions Method
To solve the system of linear equations in two variables as a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 by substitution method, you need to find the value of one variable in terms of other variable from any one of the equation and then put this value in other equation. After this substitution, you will get a linear equation in one variable, which is very easy to solve by algebraic operations on both sides.
To understand the substitution method of solving system of linear equations, let’s solve the equations as below.
For example: Solve the system of equations as
Equation 1: 2x + 3y = 9
Equation 2: x – y = 3
From Equation 2, you get x = y + 3.
Now, put this value of x in Equation 1,
2(y + 3) + 3y = 9
⇒ 2y + 6 + 3y = 9
⇒ 5y = 3
⇒ y = 3/5 and then x = y + 3 = 3/5 + 3 = 18/5
Hence, x = 18/5 and y = 3/5 are the solution of given equations.
Solving System of Linear Equations in Two Variables by Cross Multiplication Method
To solve the system of linear equations in two variables as a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 by cross multiplication method, you need to do following steps.
Number of Solutions of System of Linear Equations in Two Variables
The standard form of linear equations is
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
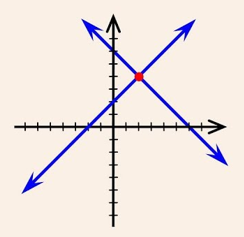
For Unique Solution (Only One Solution) or Consistent System of Equations, in this case the graph of the linear equations is intersected lines.
Required condition to be Unique solution is
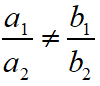
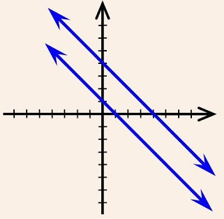
For No Solution or Inconsistent System of Equations, in this case the graph of the linear equations is parallel lines.
Required condition to be No solution is
For Many Solution or Consistent System of Equations, in this case the graph of the linear equations is coincident lines.
Required condition to be Many solution is
Word Problems on System of Linear Equations in Two Variables
To solve the system of linear equations in two variables,
- Read the word problem statement carefully and observe what is given and what is need to be found.
- Represent the unknown by the variables as x, y, …….
- Translate the given problem statement into mathematical statements.
- Form the linear equation in one variable according to requirement using the conditions given in the problems.
- Solve the equation for the unknown using elimination, substitution or cross multiplication methods
- Verify your answer satisfies the conditions of the problem.
Functions
In functions of SAT Algebra syllabus, you need to learn about linear functions, compositions of functions, rate of change and absolute value functions.
Linear Functions
A linear function is a linear polynomial of the form of (ax + b). The graph of a linear function is always a straight line. The linear function is denoted by f(x), g(x) or p(x) etc.
For example: f(x) = 3x + 5, g(t) = 9t – 11/5 etc.
Value of Linear Functions
The value of linear function f(x) = ax + b at x = k is when x is substituted with k in the linear function. It mean, the value of f(x) = ax + b at x = k is f(k) = ak + b.
For example: if f(x) = 9x – 7, then the value of the function at x = 2 is f(2) = 9(2) – 7 = 18 – 7 = 11.
Composition of Functions
The composition of functions is a composition of two functions in which the output of one function is the input for the second function.
The composition of functions f(x) and g(x) is fog(x) = f(g(x)) or gof(x) = g(f(x)).
For example:
If f(x) = 2x + 3 and g(x) = 5x – 7, then
fog(x) = f(g(x)) = 2(g(x)) + 3 = 2(5x – 7) + 3 = 10x – 14 + 3 = 10x – 11
gof(x) = g(f(x)) = 5(f(x)) – 7 = 5(2x + 3) – 7 = 10x + 15 – 7 = 10x + 8
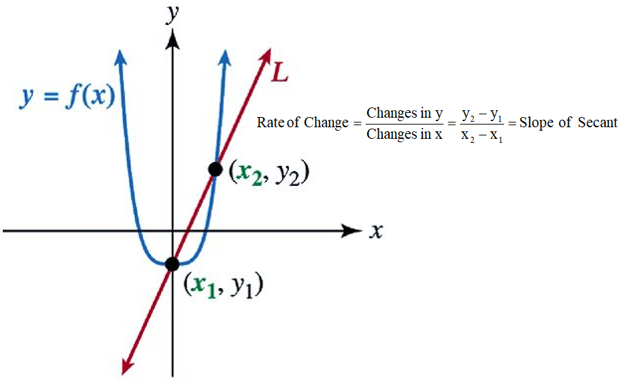
Average Rate of Change of Functions
The average rate of change of function y = f(x) on an interval x ∈ [a, b] is the measure of rate of changes of the variable y with respect to change of x.
Average Rate of Change of Linear Functions
Since the graph of a linear function is a straight line, then its average rate of change of a linear function y = f(x) is as below.
Thus, for a linear function y = ax + b, the average rate of change of linear function is slope of the line.
For example: in the equation of line y = 5x + 9, the rate of change is its slope which is equal to 5.
Average Rate of Change of Non-linear Functions
Since the graph of a non-linear function y = f(x) is not a linear, so in that case, the average rate of change of a non-linear function f(x) on an interval [a,b] is the slope of the secant line.
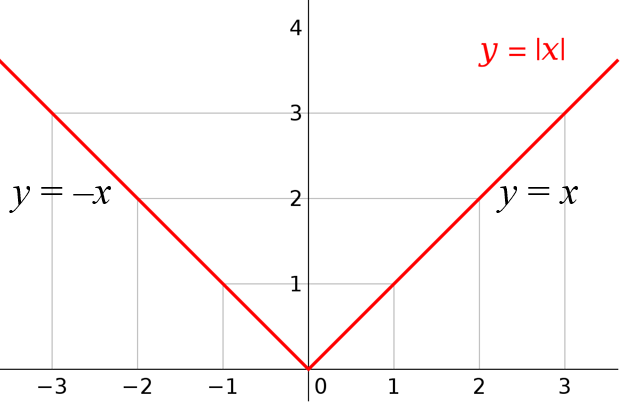
Absolute Value of Number
Absolute value of a number is its distance from zero on number line. The absolute value of a real number x is denoted by |x|.
For example: The number 5 is at a distance of 5 units from 0 and -5 is at a distance of 5 units from 0. Thus, |5| = 5 and |-5| = 5
Absolute Value Functions
The absolute value function y = |x| is defined as below.
For x ≥ 0, y = |x| = x , and
For x < 0, y = |x| = -x
Inequalities
In inequalities of SAT Algebra syllabus, you need to learn about intervals, linear inequalities, quadratic inequalities, absolute value inequalities.
What are Inequalities and Inequations?
The signs of < (Less than), ≤ (Less Than or Equal To), > (Greater Than), ≥ (Greater Than or Equal To) are called inequality and a mathematical statement which contains sign <, ≤, >, ≥ is called an inequation.
The inequality defines the comparison between two numbers or two mathematical statements
For example: 5x + 6 > 10, 3x/2 – 9 ≤ 5 etc.
Intervals
There are following types of intervals.
Open Interval : x ∈ (a, b) ⇒ a < x < b ⇒ x can take all real values after “a” till before “b”.
Close Interval : x ∈ [a, b] ⇒ a ≤ x ≤ b ⇒ x can take all real values from “a” to “b”.
Left Open Right Closed Interval : x ∈ (a, b] ⇒ a < x ≤ b ⇒ x can take all real values after “a” to “b”.
Left Close Right Open Interval : x ∈ [a, b) ⇒ a ≤ x < b ⇒ x can take all real values from “a” till before “b”.
Left Open Right Unbounded : x ∈ (a, ∞) ⇒ x > a ⇒ x can take all real values after “a” tending to infinity.
Left Close Right Unbounded : x ∈ [a, ∞) ⇒ x ≥ a ⇒ x can take all real values from “a” tending to infinity.
Left Unbounded Right Open : x ∈ (-∞, b) ⇒ x < b ⇒ x can take all real values before “b”.
Left Unbounded Right Close : x ∈ (-∞, b] ⇒ x ≤ b ⇒ x can take all real values till “b”.
Properties of Inequalities
For all real numbers a, b and c , the following are true.
Transitive Property: If a < b and b < c, then a < c.
Addition and Subtraction Property: If a < b, then a + k < b + k and a – k < b – k.
Multiplication and Division Property: If a < b and k is positive, then ak < bk and a/k < b/k.
If a < b and k is negative, then ak > bk and a/k > b/k.
Solving Inequalities
Solving inequalities is same as solving equations with one very important exception that whenever you multiply or divided both sides by a negative number, then the inequality sign will be reversed. And, use all the properties of inequalities.
Solving Linear Inequalities in One Variable
Linear inequalities in one variable are of the following forms.
ax + b > 0,
ax + b ≥ 0,
ax + b < 0,
ax + b ≤ 0.
Solving linear inequalities of one variable is same as the solving equation with doing algebraic operations and represent the solution of inequations using intervals or on number line.
Solving Linear Inequalities in Two Variables
Linear inequalities in two variables are of the following forms.
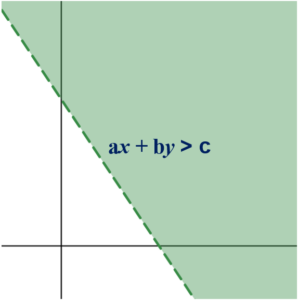
ax + by > c,
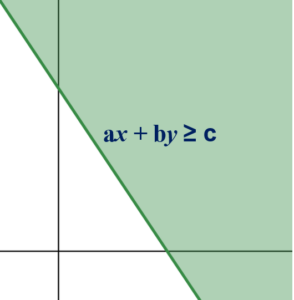
ax + by ≥ c,
ax + by < c,
ax + by ≤ c.
Now, the solution of linear inequalities in two variables is done by using graphing the linear inequalities.
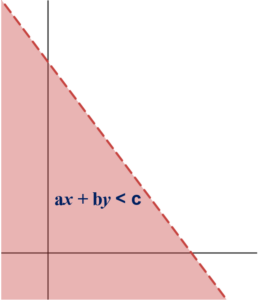
The solution of the linear inequality of the form of ax + by > c contains all the points on the shaded region as below. In this solution, the solution of ax + by = c is excluded, hence the graph of ax + by = c is represented as dotted line.
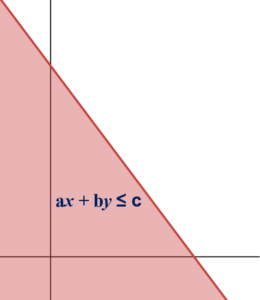
The solution of the linear inequality of the form of ax + by ≥ c contains all the points on the shaded region as below. In this solution, the solution of ax + by = c is included, hence the graph of ax + by = c is represented as solid line.
The solution of the linear inequality of the form of ax + by < c contains all the points on the shaded region as below. In this solution, the solution of ax + by = c is excluded, hence the graph of ax + by = c is represented as dotted line.
The solution of the linear inequality of the form of ax + by ≤ c contains all the points on the shaded region as below. In this solution, the solution of ax + by = c is included, hence the graph of ax + by = c is represented as solid line.
Solving System of Linear Inequalities in Two Variables
In solving the system of linear inequalities, you need to draw the regions of solutions of both linear inequalities as discussed above and then the solutions of linear inequalities is the intersection of the regions of both solutions region.
ax + by > c,
ax + by ≥ c,
ax + by < c,
ax + by ≤ c.
To understand better, let’s solve one example.
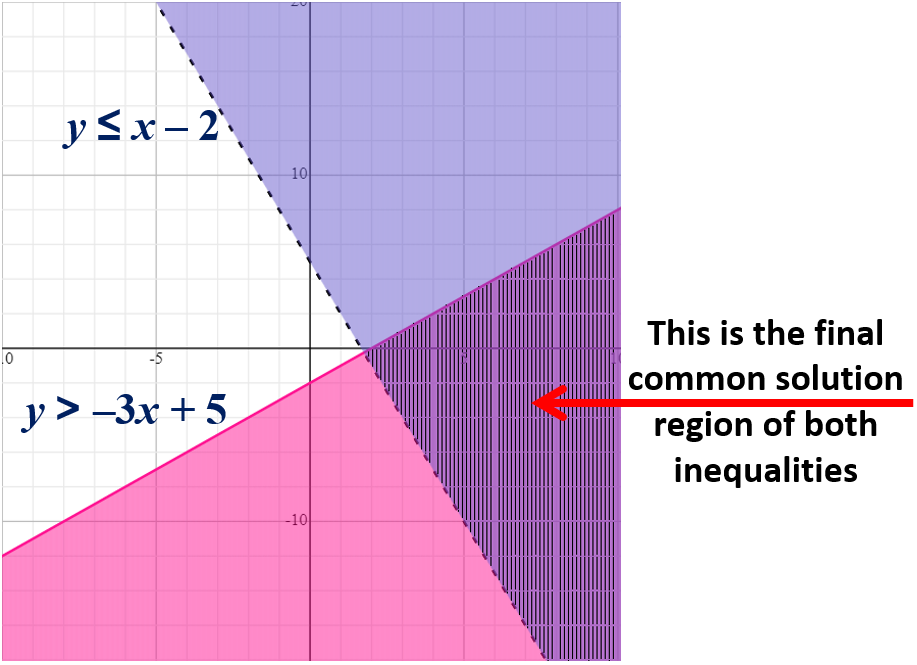
For example: Solve the system of inequalities of inequalities y ≤ x – 2 and y > -3x + 5.
First, draw the solution region of the inequality y ≤ x – 2 and then draw the solution region of the inequality y > -3x + 5.
Now, the intersection of both region is the solution region of both the given inequalities.
Absolute Value Inequalities
The solution of absolute value inequalities is done by following rules.
- If |x| < a, then -a < x < a.
- If |x| ≤ a, then -a ≤ x ≤ a.
- If |x| > a, then x < -a or x > a.
- If |x| ≥ a, then x ≤ -a or x ≥ a.
- If |ax + b| < c, then -c < ax + b < c ⇒ -c – b < ax < c – b ⇒ (-c – b)/a < x < (c – b)/a
- If |ax + b| ≤ c, then -c ≤ ax + b ≤ c ⇒ -c – b ≤ ax ≤ c – b ⇒ (-c – b)/a ≤ x ≤ (c – b)/a
- If |ax + b| > c, then ax + b < -c or ax + b > c ⇒ ax < -c – b or ax > c – b ⇒ x < (-c – b)/a or x > (c – b)/a
- If |ax + b| ≥ c, then ax + b ≤ -c or ax + b ≥ c ⇒ ax ≤ -c – b or ax ≥ c – b ⇒ x ≤ (-c – b)/a or x ≥ (c – b)/a
Quadratic Inequalities
Quadratic inequalities are of the following forms.
ax2 + bx + c > 0,
ax2 + bx + c ≥ 0,
ax2 + bx + c < 0,
ax2 + bx + c ≤ 0.
To solve these quadratic inequalities, first you need to find the roots of the quadratic equation ax2 + bx + c = 0 and then write the quadratic equation as product of its two factors.
Let α and β are the roots of quadratic equation.
Then, ax2 + bx + c = a(x – α)(x – β), where a > 0.
Now, you need to solve the quadratic inequalities as below.
(x – α)(x – β) > 0,
(x – α)(x – β) ≥ 0,
(x – α)(x – β) < 0,
(x – α)(x – β) ≤ 0.
Now, the solution of quadratic inequalities is done by using following rules.
- If (x – α)(x – β) < 0, then α < x < β.
- If (x – α)(x – β) ≤ 0, then α ≤ x ≤ β.
- If (x – α)(x – β) > 0, then x < α or x > β.
- If (x – α)(x – β) ≥ 0, then x ≤ α or x ≥ β.
SAT Math Reference Sheet | Problem Solving Data Analysis
NOTE : (Practice Questions are Given on Home Page of This Website.)
In SAT Math Problem Solving Data Analysis, there are following SAT Math Topics are included. You need to read this SAT Math Reference Sheet carefully to become a master in Problem Solving Data Analysis topics of SAT Math. This SAT Math Data Analysis Notes is a list of formulas to know for sat.
- Ratio and Proportions
- Ratios
- Rates
- Proportions
- Percentage
- Definition of Percentage
- Percentage of Change
- Word problems of Percentage
- Statistics
- Mean
- Median
- Mode
- Range
- Probability
- Definition of Probability
- Mutually Exclusive Events
- Dependent Events
- Independent Events
- Addition Rule of Probability
- Product Rule of Probability
- Unit Conversion
- Volume
- Capacity
- Capacity to Volume Conversion
- Density
Let’s learn these SAT math topics of Problem Solving Data Analysis, one by one.
Ratios and Proportions
In ratio and proportions of SAT Data Analysis syllabus, you need to learn the concepts of ratios, rates and proportions.
Ratios
A ratio is a comparison of two quantities of same units by their division.
If a and b are two quantities of same unit, then the ratio can be a : b or a/b.
For example: Ratio of 3 kg to 300 gm is 3kg / 300 gm = 3000 / 300 = 10 / 1 = 10 : 1.
If a number x is divided into the ratio a : b, then first number is ax/(a + b) and other quantity is bx/(a + b).
For example:
If 100 is divided into ratio of 13 : 12, then
the first number is 100 × 13 / (13 + 12) = 100 × 13 / 25 = 4 × 13 = 52
the second number is 100 × 12 / (13 + 12) = 100 × 12 / 25 = 4 × 12 = 48
Rates
A rate is a comparison of two quantities of different units by their division.
For example: If a car is running a distance of 120 km in 2 hours, then its rate is 120 km / 2 hour = 60 km/hour.
Proportions
An equality of ratios is known as proportion.
If the ratios a / b and c / d are equal, means a / b = c / d, then a, b, c, d are in proportion.
If four numbers a, b, c, d are in proportion, then first and last numbers a and d are extremes and second and third numbers b and c are means.
Since four numbers a, b, c, d are in proportion, then a/b = c/d ⇒ ad = bc ⇒ Product of Extremes = Product of Means.
Percentage
In percentage of SAT Data Analysis syllabus, you need to learn the concepts of percentage, percentage of change.
Percent
A percent means per “cent”, it means a quantity in per 100 is called percent.
For example: if a student get 85 marks in his test of 100 marks, then the percent of marks obtained by student is 85%.
To convert a percentage into fraction or decimal, remove the percentage (%) sign and divide the number by 100 and then simplify it.
For example: 50% = 50/100 = 1/2, 45% = 45/100 = 0.45 etc.
To convert a fraction or a decimal into percentage, multiply the fraction or decimal with 100 and put the sign of percentage (%) with it.
For example: 3/4 = (3/4 × 100)% = 75%, 12/5 = (12/5 × 100)% = 240%.
Percentage of Change
When a quantity increases or decrease from its original amount, then this called increase or decrease and if the increase or decrease is converted into percentage, then it is known as percentage of change.
Percentage Increase = (Amount of Increasing / Original Amount ) × 100 %
Percentage Decrease = (Amount of Decreasing / Original Amount ) × 100 %
Word Problems on Percentage
In the word problems of percentage, there is an equation is formed as below.
Let x% of M is N. Then, the equation is M × x / 100 = N.
Out of these three quantities, two quantities are known and one of them is unknown.
Thus, you need to ask three types of questions.
- Finding the percent of an amount (Find N)
- Finding the percentage (Find x)
- Finding the whole (Find M)
Statistics
In statistics of SAT Data Analysis syllabus, you need to learn the concepts of mean, median, mode and range. Mean, median and mode are known as three measures of central tendency in statistics.
Mean
A mean of a data set is the sum of all observations divided by the number of observations. The mean is also known as arithmetic mean or average.
Median
A median of a data set is the middlemost observation when the the observations are arranged in ascending or descending order.
If the number of observations in the set is odd, then there is only one middlemost observation, hence this middlemost is the median.
If the number of observations in the set is even, then there are two middlemost observations, hence the mean of these middlemost observations is the median.
Mode
A mode of a data set is the observation which has highest frequency. Some set of data have more than one mode, and others have no mode.
Range
In a data set, the difference between the highest value observation and lowest value observation is known as range of the data set.
For example: Find the mean, median, mode, and range of the data set {132, 149, 152, 164, 164, 175}.
Mean = (132 + 149 + 152 + 164 + 164 + 175) / 6 = 156
Since the data set is already in ascending order and the number of observations is even, hence its middlemost observations are 152 and 164. Hence,
Median = (152 + 164) / 2 = 158
Since the observation 164 repeats two times, then 164 has highest frequency.
Mode = 164
In the data set, 132 is the lowest and 175 is the highest value. Then,
Range = 175 – 132 = 43
Probability
In probability of SAT Data Analysis syllabus, you need to learn about the definition of probability, mutually exclusive events, dependent and independent events, addition rules of probability, product of probability, mutually exclusive events, dependent and independent events probability etc.
Definition of Probability
In our daily life, many events cannot be predicted you can measure only the chance of an event to occur. Thus, the probability is a measure of the likelihood of an event to occur.
In a trial, an outcome is one of the possible results that can occur as a result of a trial. Thus, the probability of an even A is denoted as P(A) and it is defined as
Mutually Exclusive Events
Two events which do not occur simultaneously known as mutually exclusive events.
If A and B are mutually exclusive events, then P(A ∩ B) = 0
Dependent Events
Two events in which the occurrence of one event affect the occurrence of other known as dependent events.
If A and B are dependent events such that the event A is already occurred, then P(A ∩ B) = P(A) × P(B/A) and when the event B is already occurred, then P(A ∩ B) = P(B) × P(A/B).
Independent Events
Two events in which the occurrence of any event does not affect the occurrence of other known as independent events.
If A and B are independent events P(A ∩ B) = P(A) × P(B).
Addition Rule of Probability
If A and B are events, then the probability of occurrence of event A or B or both is
P(A or B) = P(A ∪ B) = P(A) + (B) – P(A ∩ B)
If A and B are mutually exclusive events [ P(A ∩ B) = 0 ], then
P(A or B) = P(A ∪ B) = P(A) + P(B)
Product Rule of Probability
If A and B are independent events, then the probability of occurrence of event A and B is
P(A and B) = P(A ∩ B) = P(A) × P(B)
If A and B are dependent events, then the probability of occurrence of event A and B is
P(A and B) = P(A ∩ B) = P(A) × P(B/A)
Unit Conversion
In unit conversion of SAT Data Analysis syllabus, you need to learn how to convert of some units.
You can use conversion factors to convert a unit of measure from one system to another. Sometimes you may need to use two or more conversion factors
Volume Conversion
Volume is the total amount of space that is covered by an object which can be solid or hollow. The unit of volume is cubic units like cm3, m3.
Capacity Conversion
Volume is the total amount of space that is covered by an object which can be hollow only. The unit of volume is cubic units like litre, gallons, etc.
Capacity to Volume Conversion
The conversion of litre to cm3 is 1 litre = 1000 cm3.
Formulas to Remember for SAT : Density
Density is a measure of mass per unit volume. Hence,
Density = Mass / Volume
SAT Math Cheat Sheet | Passport to Advance Math
NOTE : (Practice Questions are Given on Home Page of This Website.)
In SAT Math Passport to Advance Math, there are following SAT Math Topics are included. You need to read this SAT Math Cheat Sheet carefully to become a master in Passport to Advance Math topics of SAT Math. This SAT Advance Math Notes is a list of formulas to remember for sat.
- Exponent
- Laws of Exponents or Exponent Rules
- Polynomials
- Addition of Polynomials
- Subtraction of Polynomials
- Multiplication of Polynomials
- Special Product of Polynomials
- Division of Polynomials
- Factorization of Polynomials
- LCM and HCF of Polynomials
- Remainder Theorem
- Factor Theorems
- Quadratic Expression and Equations
- Quadratic Expression or Functions
- Quadratic Equations
- Factorization of Quadratic Polynomials
- Solving Quadratic Equations
- Solving Quadratic Equations by Factorization
- Quadratic Formula
- Discriminant of Quadratic Equations
- Solving Quadratic Equations by Quadratic Formula
- Graph of Quadratic Polynomials
- System System Containing Linear and Quadratic Equations
- Radical Expression & Equations
- Radicals
- Product & Quotient Property of Radicals
- Solving Radicals Equations
- Trigonometry
- Degree and Radian Measurements of Angles
- Trigonometric Ratios of Acute Angles
- Trigonometric Quotient Identities
- Trigonometric Reciprocal Identities
- Trigonometric Identities
- Trigonometric Values
- Trigonometric Values of Complementary Angles
Let’s learn these SAT math topics of Passport to Advance Math, one by one.
Exponents and Powers
An Exponent and Powers are ways to represent very large numbers or very small numbers in a simplified form.
For example, a very large number 1000000000000 (12 zeroes) can be simplified form as 1012, where 12 is the exponent and 10 is the base. The whole expression 1012 is called as power.
Similarly, a very small number 0.000000000001 can be simplified as 10-12 where -12 is the exponent and 10 is the base.
In exponents and powers of SAT Advance Math syllabus, you need to learn laws of exponents.
Laws of Exponents or Exponent Rules
For all integers m and n and any nonzero numbers a and b, the following properties exponent rules:
- Exponent Rules 1: a0 = 1
- For example: (2xy)0 = 1
- Exponent Rules 2: a1 = a
- For example: 101 = 10
- Exponent Rules 3: am × an = am + n
- For example: 25 × 24 = 25 + 4 = 512
- Exponent Rules 4: am ÷ an = am – n
- For example: 25 ÷ 24 = 25 – 4 = 2
- Exponent Rules 5: (am)n = amn
- For example: (25)4 = 25 × 4 = 220
- Exponent Rules 6: am × bm = (ab)m
- For example: 25 × 35 = 105 = 100000
- Exponent Rules 7: (a / b)m = am / bm
- For example: (2 / 3)5 = 25 / 35 = 32 / 243
- Exponent Rules 8: a-n = 1 / an
- For example: 2-2 = 1 / 22 = 1 / 4
- Exponent Rules 9: (a / b)-n = (b / a)n = bn / an
- For example: (2 / 3)-2 = (3 / 2)2 = 32 / 22 = 9 / 4
Important Formulas for SAT : Polynomials
An algebraic expression p(x) of the form of p(x) = anxn + an-1xn-1 + an-2xn-2 + … + a2x2 + a1x + a0, where a0, a1, a2, …, an are real numbers and n is a non-negative integers.
Polynomials that have only one term are called monomials (Ex: 3x, -5x 3x/2, etc.).
Polynomials that have two unlike terms are called binomials (Ex: 3x + 6, 6x – 9y, -7y + 6 etc.).
Polynomials that have three unlike terms are called trinomials (Ex: 3x + 5y + 9, -9a – 6b + 5c etc.).
Terms such as 3x2 and −2x2 are called like terms because they have the same variable to the same power.
In polynomials of SAT Advance Math syllabus, you need to learn addition, subtraction, multiplication and division of polynomials, factorization of polynomials, LCM and HCF of polynomials, remainder theorem and factor theorem.
Addition of Polynomials
To add two or more polynomials, you need to add the coefficient of like terms.
For example:
(5x2 + 3x + 9) + (8x3 + 7x2 – 9x – 7) = 8x3 + (5 + 7)x2 + (3 – 9)x + (9 – 7) = 8x3 + 12x2 – 6x + 2
Subtraction of Polynomials
To subtract a polynomial from other, you need to subtract the coefficient of like terms.
For example:
(8x3 + 7x2 – 9x – 7) – (5x2 + 3x + 9) = 8x3 + (7 – 5)x2 + (- 9 – 3)x + (- 7 – 9) = 8x3 + 2x2 – 12x – 16
Multiplication or Product of Polynomials
To multiply two or more polynomials, you need to use the distributive property of multiplication over addition or subtraction and you need to use some laws of exponents.
For example:
8x3(5x2 + 3x + 9) = (8x3 × 5x2) + (8x3 × 3x) + (8x3 × 9) = 40x5 + 24x4 + 72x3
Special Product of Polynomials
To find the special product of polynomials, you need to use following algebraic identities.
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- (a + b)(a – b) = a2 – b2
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
- (a + b)3 = a3 + b3 + 3ab(a + b)
- (a – b)3 = a3 – b3 – 3ab(a – b)
For example:
(8x + 3y)2 = (8x)2 + 2(8x)(3y) + (3y)2 = 64x2 + 48xy + 9y2
SAT Given Formulas : Division of Polynomials
To divide a polynomial by a monomial, divide each term by the monomial, add the results, and simplify.
For example:
Simplify (5x2 + 3x + 9) ÷ 2x
To divide a polynomial function f(x) by (ax + b) , you need to use long division, which is similar to long division in arithmetic, can be used to find quotient q(x) and remainder R.
For example: Divide (x3 + 2x2 – 5x + 9) ÷ (x – 2)
Factorization of Polynomials
A monomial is in factored form when it is expressed as the product of prime numbers and variables, and no variables has an exponent greater than 1.
For example: 102a2b4 = 2 × 3 × 17 × a × a × b × b × b × b.
To factor a polynomial, always look first for GCD (Greatest Common Factor) of all the terms. If there is a GCF, factor it first.
For example: x4 + x3 – x2 = x2(x2 + x – 1)
LCM and HCF of Polynomials
The HCF (Highest Common Factor) of two or more polynomials is the greatest polynomial that is a factor of each polynomial.
To find the HCF of two or more polynomial, take the smallest power of each prime factor and multiply.
The LCM (Least Common Multiple) of two or more polynomials is the least polynomials that is a common multiple of two or more polynomials.
To find the LCM of two or more polynomials, take the largest power of each prime factor and multiply.
For example:
Find the HCF and LCM of (x – y)2(x + y) and (x – y)(x + y)3.
(x – y)2(x + y) = (x – y) × (x – y) × (x + y)
(x – y)(x + y)3 = (x – y) × (x + y) × (x + y) × (x + y)
HCF = (x – y)(x + y)
LCM = (x – y)2(x + y)3
Remainder Theorem
Let ‘p(x)‘ be any polynomial of degree greater than or equal to one and a be any real number.
If a polynomial p(x) is divided by a linear polynomial (x – a), then the remainder is constant polynomial p(a) = r.
For example:
Find the remainder when the polynomial p(x) = 3x2 + 6x – 8 is divided by (x – 1).
Required remainder is P(1) = 3 + 6 – 8 = 1
Factor Theorem
Let ‘p(x)‘ be any polynomial of degree greater than or equal to one and a be any real number such that p(a) = 0, then (x – a) is a factor of p(x).
For example:
Check whether (x – 1) is a factor of the polynomial p(x) = 3x2 + 5x – 8.
Since P(1) = 3 + 5 – 8 = 0, then (x – 1) is a factor of the polynomial p(x) = 3x2 + 5x – 8.
Quadratic Expressions and Equations
In quadratic expression and equations of SAT Advance Math topics, you need to learn about quadratic expressions or functions, quadratic equations, factorization of quadratic polynomials, solving quadratic equations, quadratic formulas, discriminant of quadratic equations, system of linear and quadratic equations, graph of quadratic polynomials and radical expressions etc.
Quadratic Expression or Function
A polynomial of the form of f(x) = ax2 + bx + c, where a ≠ 0, is known as quadratic polynomial or quadratic expression of quadratic function.
Quadratic Equation
An equation of the form of ax2 + bx + c = 0, where a ≠ 0, is known as quadratic equation.
The solutions of a quadratic function are the values of x for which f(x) = ax2 + bx + c. Solutions of functions are also called roots or zeros of the function.
Factorization of Quadratic Polynomials
A quadratic polynomial of the form of x2 + bx + c can be factorized as below.
If x2 + bx + c = x2 + (m + n)x + mn, where b = m + n and c = mn, then its factor form is x2 + bx + c = (x + m)(x + n).
For example: x2 + 5x + 6 = x2 + (3 + 2)x + (3 × 2) = (x + 3)(x + 2)
A quadratic polynomial of the form of ax2 + bx + c can be factorized as below.
If ax2 + bx + c = pqx2 + (ps + qr)x + rs, where a = pq, b = ps + qr and c = rs, then its factor form is ax2 + bx + c = (px + r)(qx + s).
For example: 5x2 + x – 4 = (5 × 1)x2 + (5 × 1 + 1 × -4)x + (-4 × 1) = (5x – 4)(x + 1)
Solving Quadratic Equations
To solve a quadratic equation p(x) = ax2 + bx + c = 0, you need to use factorization of the quadratic function or use a quadratic formula.
Solving Quadratic Equations by Factorization
If the product a b⋅ = 0 , then either a = 0 , b = 0 , or both a and b equal zero. Factoring and zero product property allow you to solve a quadratic equation by converting it into two linear equations.
To solve a quadratic equation p(x) = ax2 + bx + c = 0 by factorization, first you need to factorize the quadratic function and then equate each factor as zero and then find the values of x.
For example:
Solve 5x2 – 14x – 3 = 0.
⇒ 5x2 – 15x + x – 3 = 0
⇒ 5x(x – 3) + 1(x – 3) = 0
⇒ (5x + 1)(x – 3) = 0
⇒ (5x + 1) = 0 or (x – 3) = 0
⇒ x = -1/5 or x = 3
SAT Formulas : Quadratic Formula
If ax2 + bx + c = 0, where a ≠ 0, then the formula to find the values of x is known as quadratic formula, which is
Discriminant of Quadratic Equations
In a quadratic formula, the expression under the radical sign (b2 – 4ac) is called the discriminant of the quadratic equation.
The value of the discriminant can be used to determine the number of real roots for the quadratic equation.
Solving Quadratic Equations by Quadratic Formula
To solve a quadratic equation p(x) = ax2 + bx + c = 0 by quadratic formula, you need to use the quadratic formula.
For example:
Solve 2x2 – 4x – 3 = 0.
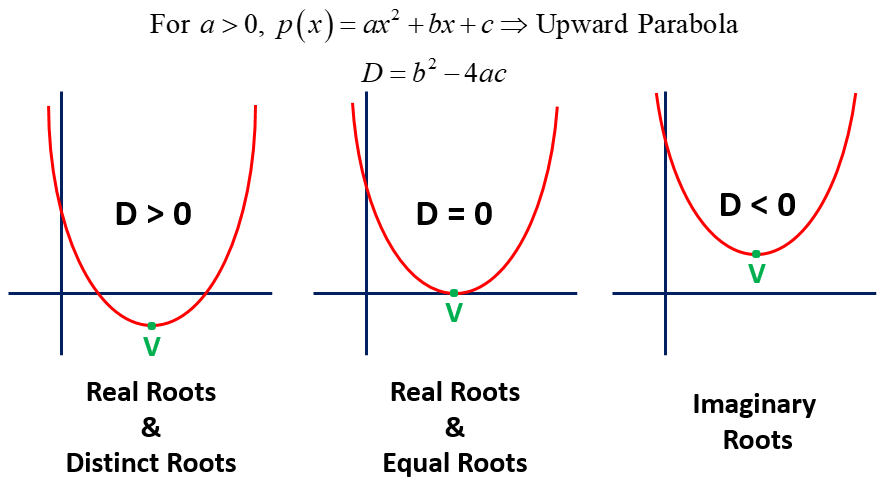
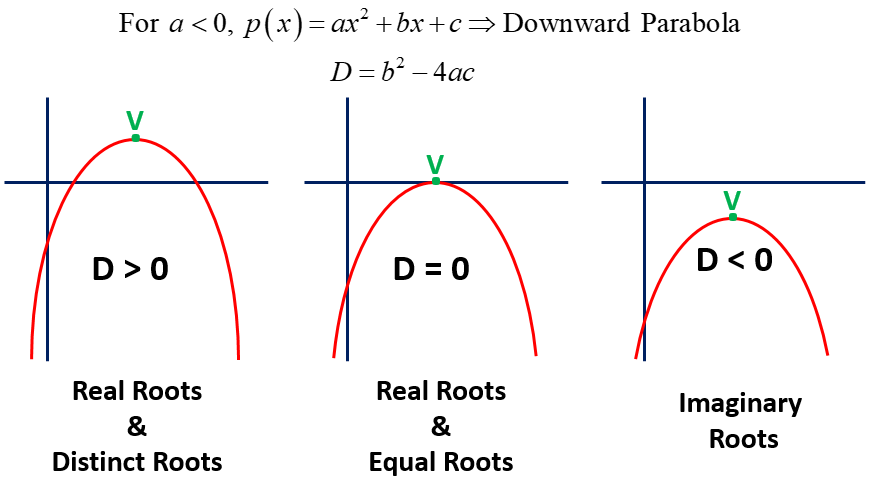
Graph of Quadratic Polynomial
The graph of a quadratic polynomial y = p(x) = ax2 + bx + c, is a parabola. The parabola can be upward or downward, it depends on the sign of ‘a‘ (coefficient of x2).
If a > 0 , the graph opens upward and the vertex is the minimum point.
If a < 0 , the graph opens downward and the vertex is the maximum point.
The maximum or minimum point of a parabola is called the vertex, whose the coordinate of the vertex is V(-b/2a, -D/4a).
In this case, the maximum and minimum values of the quadratic polynomial is as below.
In this case, the maximum and minimum values of the quadratic polynomial is as below.
Solving Systems Consisting Linear and Quadratic Equations
A system containing only quadratic equations or a combination of linear and quadratic equations in the same two variables is called a quadratic system.
The substitution and elimination methods used to solve linear systems can also be used to solve quadratic systems algebraically.
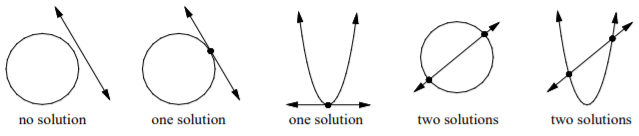
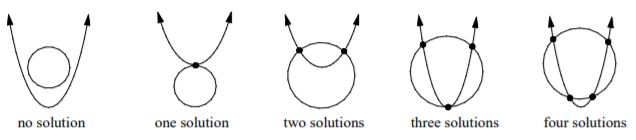
You can use graphs to find the number of real solutions of a quadratic system.
If the graphs of a system of equations are a quadratic and a linear, the system will have 0, 1, or 2 solutions.
If the graphs of a system of equations are two quadratic equations, the system will have 0, 1, 2, 3, or 4 solutions.
Radical Expressions and Equations
In radicals expression and equations of SAT Advance Math topics, you need to learn about radicals and how to solve the equations containing radicals.
SAT Formula Sheet : Radicals
For any real numbers x or a, and any positive integer n , if xn = a, then x is an nth root of a, it means x = .
The symbol is called a radical.
The term is also written as (a)1/n.
Product and Quotient Property of Radicals
Solving Radicals Equations
An equation which contains a radical with a variable in the radicand is called a radical equation. To solve such an equation, first isolate the radical on one side of the equation. Then square each side of the equation to eliminate the radical.
For example:
SAT Math Checklist : Trigonometry
In trigonometry of SAT Advance Math topics, you need to learn about degree and radian measurement of angles, basic definition of trigonometric ratios, trigonometric values, trigonometric identities, trigonometric values of complementary angles etc.
Degree and Radians Measurement of Angles
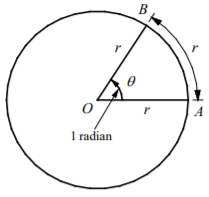
One radian is the measure of a central angle θ whose intercepted arc has a length equal to the circle’s radius.
In the figure below, if length of the arc AB = OB = OA = r, then m ∠AOB = 1 radian.
To convert an angle in degree into radian, we need to multiply π/180 to the degree.
For example: 30 degree = 30 x π/180 = π/6 radian.
To convert an angle in radian into degree, we need to multiply 180/π to the degree.
For example: π/6 radian = π/6 x 180/π = 30 degree.
Trigonometric Ratios of Acute Angles
In trigonometry, we study the relation between the sides and angles of a right triangle. For this, six trigonometric ratios, sine, cosine, tangent, cosecant, secant, and cotangent (their abbreviations are sin, cos, tan, csc, sec, and cot, respectively) are defined as below.
Trigonometric Quotient Identities
tanθ = sinθ / cosθ and cotθ = cosθ / sinθ
Trigonometric Reciprocal Identities
sinθ × cosecθ = 1 or sinθ = 1/ cosecθ and cosecθ = 1/ sinθ.
cosθ × secθ = 1 or cosθ = 1/ secθ and secθ = 1/ cosθ.
tanθ × cotθ = 1 or tanθ = 1/ cotθ and cotθ = 1/ tanθ.
Trigonometric Identities
sin2θ + cos2θ = 1
sec2θ – tan2θ = 1
cosec2θ – cot2θ = 1
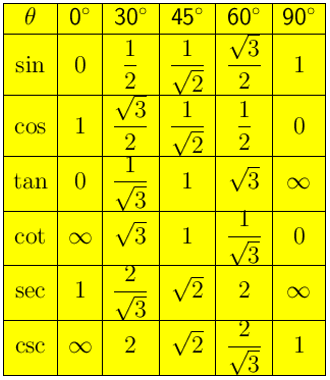
Trigonometric Values
There are some specific trigonometric values of certain angles which are given below in trigonometric table.
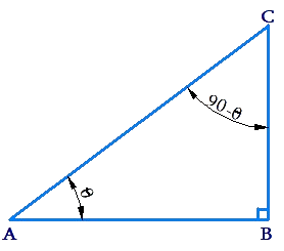
Trigonometric Values of Complementary Angles
sin(90o – θ) = cosθ
cos(90o – θ) = sinθ
tan(90o – θ) = cotθ
cosec(90o – θ) = secθ
sec(90o – θ) = cosecθ
cot(90o – θ) = tanθ
SAT Math Checklist Sheet | Additional Topics in Math
NOTE : (Practice Questions are Given on Home Page of This Website.)
In SAT Math Additional Topics in Math, there are following SAT Math Topics are included. You need to read this SAT Math Checklist Sheet carefully to become a master in Passport to Advance Math topics of SAT Math. This SAT Additional Topics in Math is a list of SAT Geometry formulas pdf.
- Lines and Angles
- Lines
- Line Segment
- Ray
- Angles
- Types of Angles
- Vertical Angles
- Complementary Angles
- Supplementary Angles
- Triangles
- Types of Triangles
- Special Right Triangles
- Pythagorean Theorems
- Angle Sum Theorem of Triangle
- Exterior Angle of Triangle
- Congruent Triangles
- Similar Triangles
- Area of Triangle
- Triangle Theorems
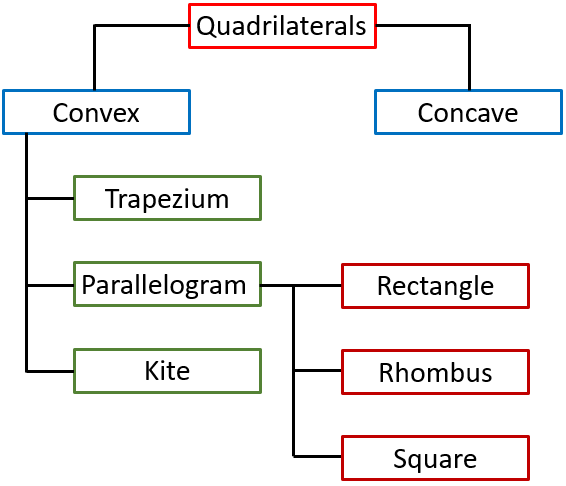
- Quadrilaterals
- Parallelograms
- Rectangle
- Squares
- Trapezium
- Regular Polygons
- Circles
- Basic Definitions
- Chords
- Tangent
- Secants
- Sector Area
- Segment Area
- Arc Lengths
- Circles Theorems
- Equations of Circles
- Surface Area Volumes
- Prism
- Pyramid
- Cuboid
- Cube
- Cylinder
- Cones
- Spheres
Lines and Angles
In Lines and Angles of SAT Geometry Topics, you need to learn about lines, line segment, ray, angles, types of angles, parallel lines intersected by transversal line etc.
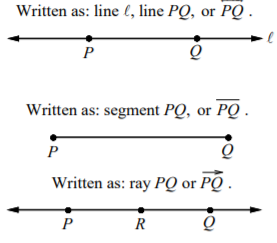
Lines
A line is a straight arrangement of points and extends in two directions, it means it does not have any endpoints. It has an infinite length. It is named by a lower-case script letter.
Line Segments
When a line has two endpoints, then this is known as line segment. Its length is defined.
SAT Math Tricks PDF : Ray
A ray is a part of a line. It has one endpoint and extends forever in one direction.
For example:
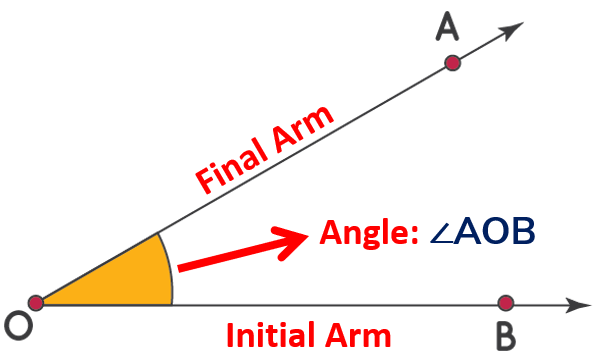
Angles
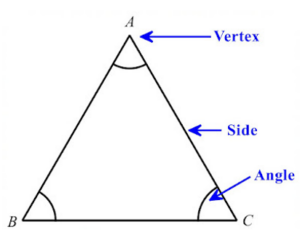
An ANGLE is the amount of rotation from initial arm to final arm which share a common endpoint. The arms are known as the sides of the angle and the common point is known is the vertex of the angle.
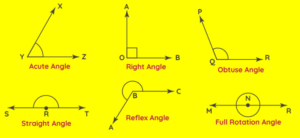
SAT Math Chapters : Type of Angles
Angles are classified according to their measures.
Acute Angles
An acute angle measures between 0 and 90.
Right Angles
A right angle measures 90.
Obtuse Angles
An obtuse angle measures between 90 and 180.
Straight Angles
A straight angle measures 180.
Reflex Angles
A reflex angle measures between 180 and 360.
Full Rotation Angles
A full rotation angle measures 360.
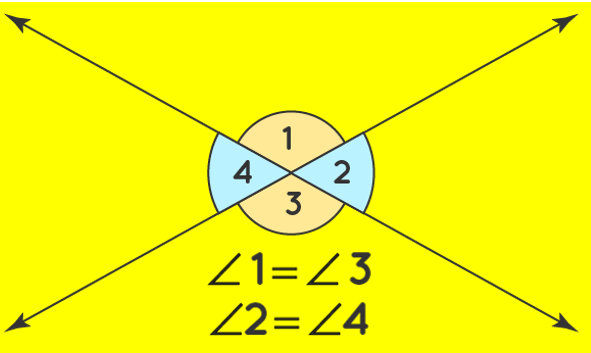
Vertical Angles
When two lines intersect, they form two pairs of vertical angles. Vertical angles are congruent.
Complementary Angles
Two angles whose measures have a sum of 90 are called complementary angles.
Supplementary Angles
Two angles whose measures have a sum of 180 are called supplementary angles.
Triangles
In Triangles of SAT Geometry Topics, you need to learn about triangles, types of triangles, angle sum theorem of triangles, exterior angle theorem of triangles, Pythagoras theorem, special right triangles, congruent triangles, similar triangles, triangle proportionality theorem, angle bisector theorem, area of triangle.
SAT Math Topics : Triangles
A triangle is a polygon with three sides. In a triangle, there are three sides (AB, BC and CA), three angles (A, B and C).
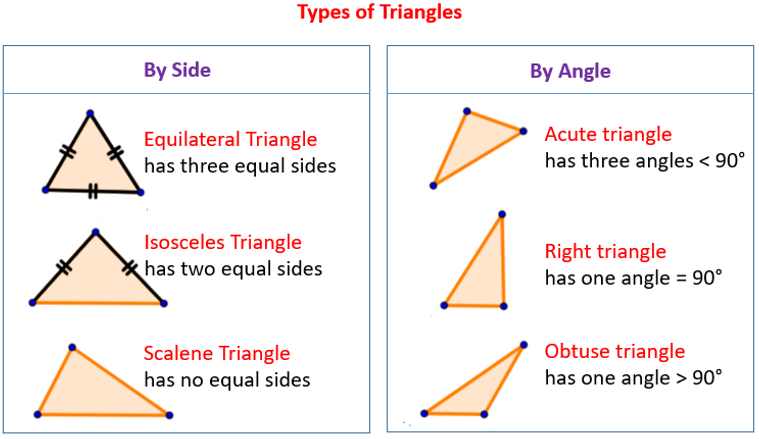
Types of Triangles
Triangles are classified as according to their sides and their angles.
According to sides, triangles are of three types as
Equilateral Triangles
A triangle in which three sides are equal is known as equilateral triangle. Hence, all the three angles are equal in the equilateral triangle.
Isosceles Triangles
A triangle in which two sides are equal is known as isosceles triangle. Hence, the two angles are equal in the isosceles triangle.
Scalene Triangles
A triangle in which no equal sides is known as isosceles triangle. Hence, the two angles are equal in the isosceles.
According to angles, triangles are of three types as
Acute Triangles
A triangle in which all the three angles are in between 0 to 90 degrees is known as acute triangle.
Right Triangles
A triangle in which one of the three angles is equal to 90 degrees is known as right triangle.
Obtuse Triangles
A triangle in which one of the three angles is in between 90 to 180 degrees is known as obtuse triangle.
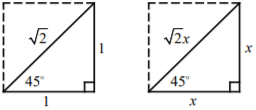
Special Right Triangles : 45∘– 45∘– 90∘ Right Triangle
A right triangle with 45∘– 45∘– 90∘ is a special triangle which is also known as isosceles right triangle.
In this triangle, the hypotenuse is √2 times as long as leg.
Special Right Triangles : 30∘– 60∘– 90∘ Right Triangle
A right triangle with 30∘– 60∘– 90∘ is a special triangle, in which the hypotenuse is √3 times as long as shorter leg.
Angles Sum Theorem of Triangle
In a triangle, the sum of all interior angles is 180∘.
In triangle ABC, m∠A + m∠B + m∠C 180∘.
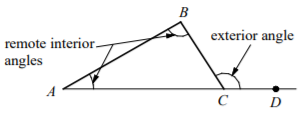
Exterior Angles Theorem of Triangle
In a triangle, an exterior angle is the sum of the measures of the two opposite interior angles.
In triangle ABC, m∠BCD = m∠A + m∠B.
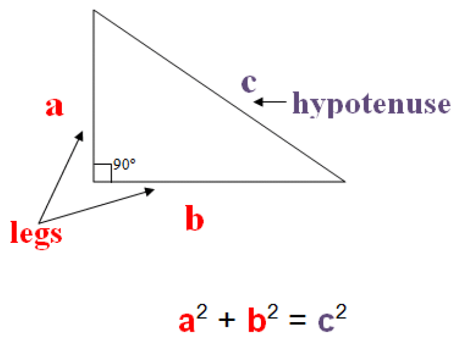
Pythagoras Theorem of Triangle
According to Pythagorean theorem, in a right triangle, the sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse.
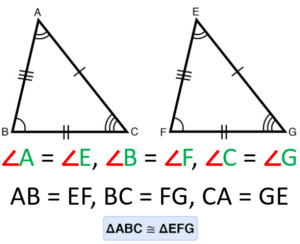
Congruent Triangles
Two triangles are said to be congruent, if the triangles are same shape and same size. And, the same shape is identified by their angles and same size is identified by their sides.
Thus, the triangles whose corresponding angles are equal and corresponding sides are equal, then the triangles are congruent.
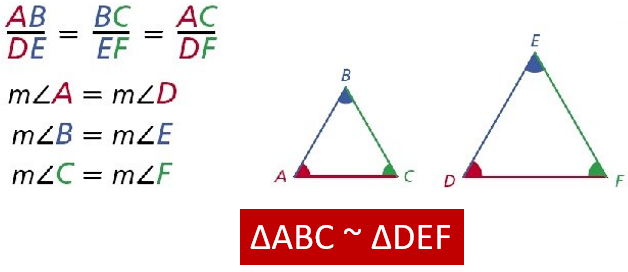
Similar Triangles
Two triangles are said to be similar, if the triangles are same shape and proportional size. And, the same shape is identified by their angles and same size is identified by their sides.
Thus, the triangles whose corresponding angles are equal and corresponding sides are proportional, then the triangles are similar.
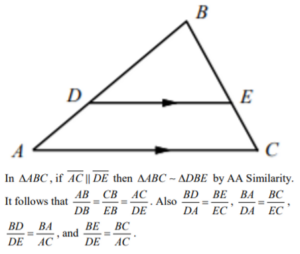
Triangle Proportionality Theorem
If a line parallel to one side of a triangle intersects the other two sides, it divides those sides proportionally.
If D and E are the midpoints of AB and BC , AC || DE, then DE = AC / 2.
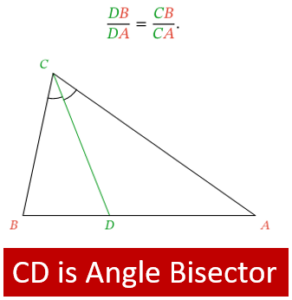
Angle Bisector Theorem
An angle bisector of a triangle splits the opposite side into the segment that have same ratio of the lengths as the sides adjacent to angle.
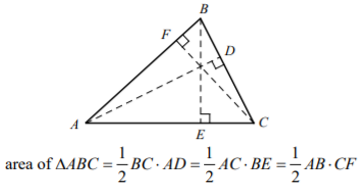
Area of Triangle
The area A of a triangle equals half the product of a base and the height to that base.
It means, A = (1/2) × Base × Height.
Quadrilaterals
In Quadrilaterals of SAT Geometry Topics, you need to learn about different quadrilaterals like parallelograms, rectangle, square, trapezium and regular polygons.
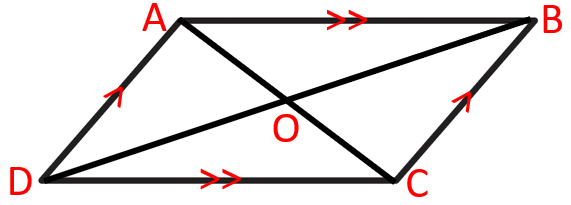
Parallelograms
A quadrilateral whose both pair of opposite sides are parallel known as parallelogram.
In parallelogram ABCD below, AB || CD and AD || BC.
Properties of Parallelograms
- Opposite sides are congruent.
- In above parallelogram ABCD, AB = CD and BC = AD.
- Opposite angles are congruent.
- In above parallelogram ABCD, Angle A = Angle C and Angle B = Angle D.
- Consecutive angles are supplementary.
- In above parallelogram ABCD, A + B = B + C = C + D = D + A = 180 degree.
- The diagonals bisect each other.
- In above parallelogram ABCD, OA = OC and OB = OD.
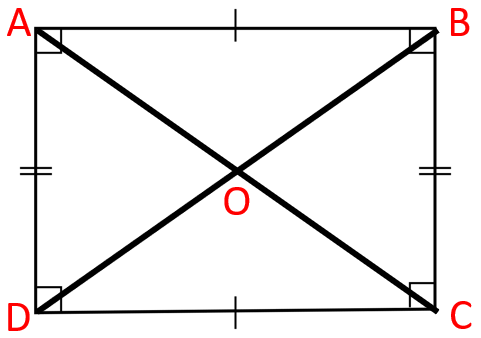
Rectangles
A parallelogram in which all the interior angles are 90 degree is known as rectangle.
Properties of Rectangle
- Opposite sides are congruent.
- In above rectangle ABCD, AB = CD and BC = AD.
- All interior angles are 90 degree.
- In above rectangle ABCD, A = B = C = D = 90 degree.
- Diagonals are equal.
- In above rectangle ABCD, AC = BD
- The diagonals bisect each other.
- In above rectangle ABCD, OA = OC and OB = OD.
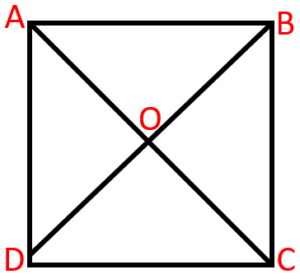
Square
A parallelogram with all sides are equal and all the interior angles are 90 degree is known as square.
Properties of Square
- All sides are congruent.
- In above square ABCD, AB = BC = CD = DA.
- All interior angles are 90 degree.
- In above square ABCD, A = B = C = D = 90 degree.
- Diagonals are equal.
- In above square ABCD, AC = BD.
- The diagonals bisect each other.
- In above square ABCD, OA = OC and OB = OD.
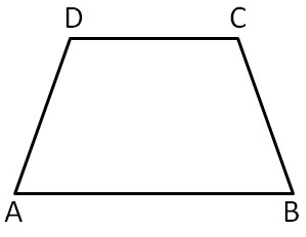
SAT Math Crash Course : Trapezium
A trapezium with one pair of opposite sides are parallel is known as trapezium.
Properties of Trapezium
- The sum of adjacent angles between parallel sides is 180 degree.
- In above trapezium ABCD, A + C = B + D = 180 degree.
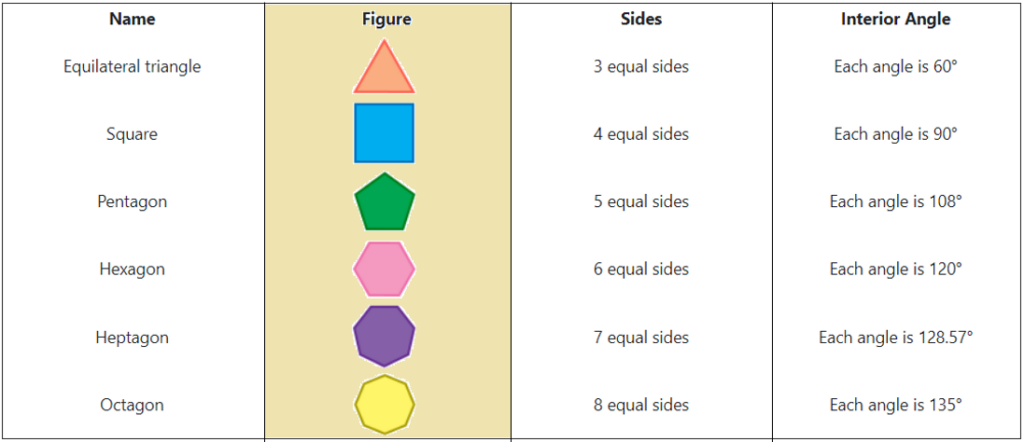
Regular Polygons
A polygon in which all the sides are equal and all the interior angles are equal is known as regular polygon.
Some examples of regular polygons as below.
Properties of Regular Polygons
- All the sides of a regular polygon are equal.
- All the interior angles are equal.
- The sum of all the interior angles of a polygon = (n − 2) × 180 degree.
- The number of diagonals in a polygon with n sides = n(n – 3)/2
- The number of triangles formed by joining the diagonals from one corner of a polygon = n – 2.
- The measure of each interior angle of n-sided regular polygon = [(n – 2) × 180°]/n
- The measure of each exterior angle of an n-sided regular polygon = 360°/n.
Circles
In Circles of SAT Geometry Topics, you need to learn about basic definition of terms related to circles like chords, tangents, secants, central angle, sectors, segments, and how to find arc lengths, and some theorems of circles, and equations of circles.
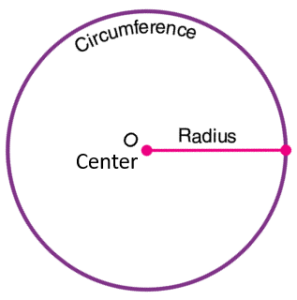
What is a Circles?
A circle is a locus of a point which moves such that its distance from a fixed point is always constant. The fixed point is known as center of the circle and the constant distance is known as radius of circle. The moving point traced the circumference of circle. OR, you can also define as a circle is the set of all points equidistant from a given point called the center. It follows from the definition of a circle that all radii are equal in measure.
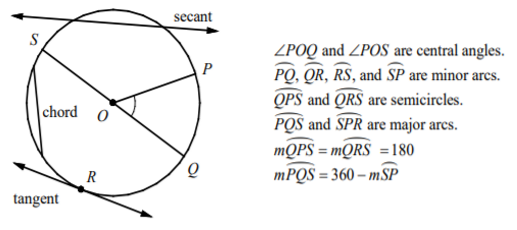
Basic Terms Related to Circles
A chord is a segment whose endpoints lie on a circle.
A secant is a line that contains a chord.
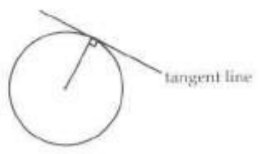
A tangent is a line in the plane of a circle, and intersects the circle at exactly one point: the point of tangency.
A central angle is an angle whose vertex is the center of the circle.
An arc is a part of a circle.
The measure of a minor arc is the measure of its central angle. The measure of a minor arc is less than 180.
The measure of a semicircle is 180.
The measure of a major arc is 360 minus the measure of its minor arc.
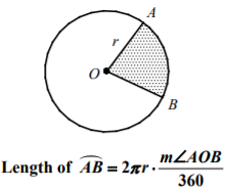
SAT Math Cheat Sheet : Arc Length
The length of an arc of circle can be found by arc length formula as below.
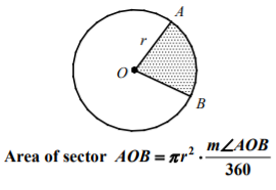
Area of Sector
The area of a sector of a circle is defined as below.
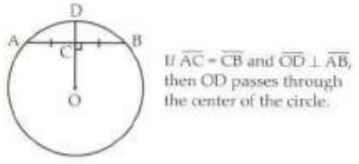
Circle Theorem 1
The perpendicular bisector of a chord of a circle passes through the center of the circle.
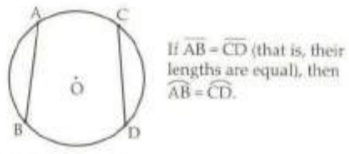
Circle Theorem 2
Equal chords have equal arcs.
Circle Theorem 3
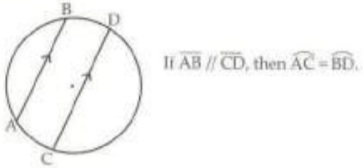
Arcs between the parallel chords are equal in length.
Circle Theorem 4
A tangent to a circle forms a right angle with the circle’s radius at the point of contact with the tangent.
Circle Theorem 5
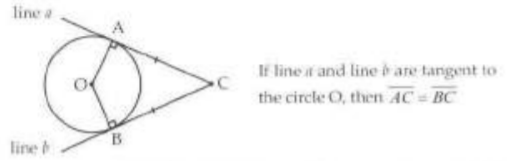
The lengths of the two tangents drawn from an external point to a circle are equal.
Circle Theorem 6
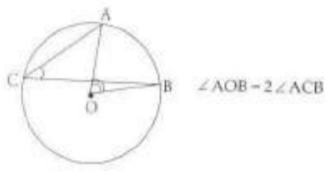
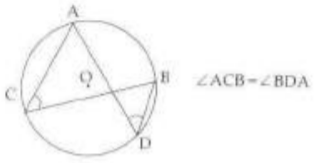
The measure of a central angle is twice the measure of any inscribed angle that intercepts the same arc.
Circle Theorem 7
Angles is same segment are equal.
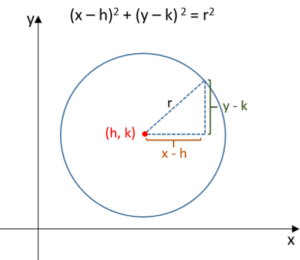
Equations of Circle
The standard equation of a circle whose center is (h, k) and radius is r, is (x – h)2 + (y – k)2 = r2.
Surface Areas Volumes
In Mensuration of 3D figures (Surface Area Volume) of SAT Geometry Topics, you need to learn about the formulas of surface area and volumes of prism, pyramid, cuboid, cube, cylinder, cones, sphere.
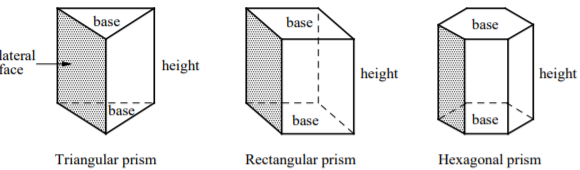
Prism
A prism is a polyhedron with two congruent and parallel faces. These two faces are called the bases of the prism.
The other faces are lateral faces.
In a prism, the lateral faces are rectangles.
The height of a prism is a segment joining the two base planes and is perpendicular to both.
Lateral Surface Area of Prism
The LSA (Lateral Surface Area) of a prism is LSA = (Perimeter of Base) × (Height).
Total Surface Area of Prism
The TSA (Total Surface Area) of a prism is TSA = LSA + 2(Base Area)
Volume of Prism
The V (Volume) of a prism is V = (Base Area) × (Height).
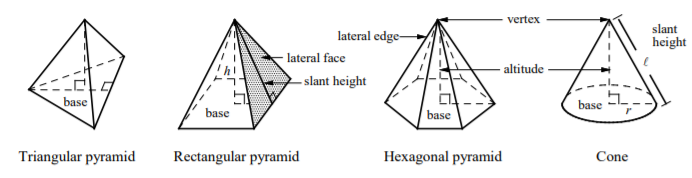
SAT Math Formulas : Pyramid
A pyramid is a polyhedron in which the base is a polygon and the lateral faces are triangles that meet at the vertex.
The height of a lateral face is called the slant height of the pyramid.
Lateral Surface Area of Pyramid
The LSA (Lateral Surface Area) of a pyramid is LSA = (1/2) × (Perimeter of Base) × (Height).
Total Surface Area of Pyramid
The TSA (Total Surface Area) of a pyramid is TSA = LSA + (Base Area)
Volume of Pyramid
The V (Volume) of a pyramid is V = (1/3) × (Base Area) × (Height).
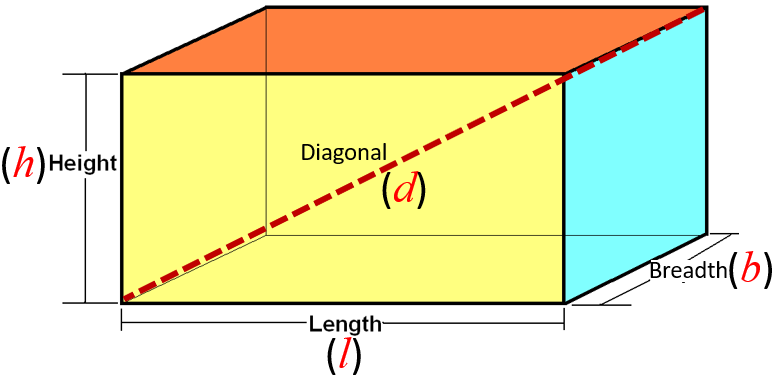
Cuboid
A cuboid is rectangular prism in which all the faces are rectangle.
Lateral Surface Area of Cuboid
The LSA (Lateral Surface Area) of a cuboid is LSA = 2 × (Height) × [(Length) + (Breadth)].
Total Surface Area of Cuboid
The TSA (Total Surface Area) of a cuboid is TSA = 2[(Length)(Breadth) + (Breadth)(Height) + (Height)(Length)].
Volume of Cuboid
The V (Volume) of a cuboid is V = (Length)(Breadth)(Height).
Diagonal of Cuboid
The d (Diagonal) of a cuboid is d = √[(Length)2 + (Breadth)2 + (Height)2].
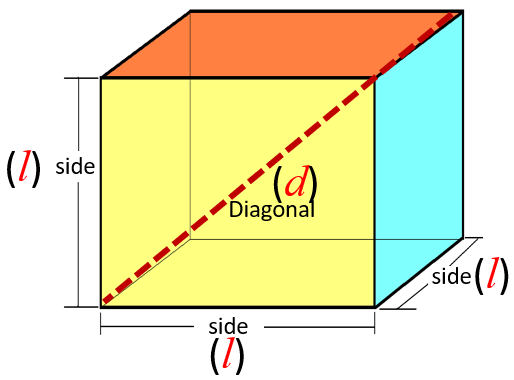
SAT Math Reference Sheet : Cube
A cube is rectangular prism in which all the faces are squares.
Lateral Surface Area of Cube
The LSA (Lateral Surface Area) of a cube is LSA = 4 × (Side)2
Total Surface Area of Cube
The TSA (Total Surface Area) of a cube is TSA = 6 × (Side)2
Volume of Cube
The V (Volume) of a cube is V = (Side)3
Diagonal of Cube
The d (Diagonal) of a cube is d = (Side)√3.
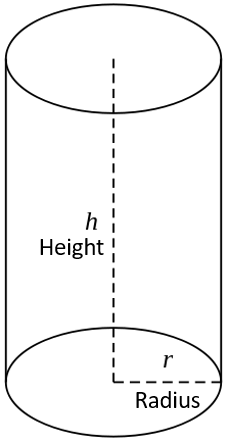
Cylinder
A cylinder is type of prism in which top and base are circle.
Curved Surface Area of Cylinder
The CSA (Curved Surface Area) of a cylinder is CSA = 2 × π × (Radius) × (Height).
Total Surface Area of Cylinder
The TSA (Total Surface Area) of a cylinder is TSA = 2 × π × (Radius) × [(Radius) + (Height)].
Volume of Cylinder
The V (Volume) of a cylinder is V = π × (Radius)2 × (Height).
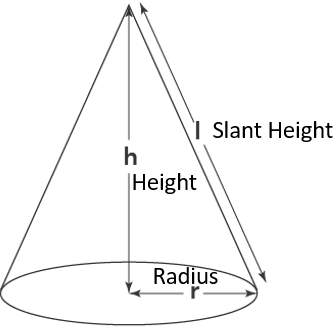
Cone
A cone is type of pyramid in which base is circle.
Curved Surface Area of Cone
The CSA (Curved Surface Area) of a cone is CSA = π × (Radius) × (Slant Height).
Total Surface Area of Cone
The TSA (Total Surface Area) of a cone is TSA = π × (Radius) × [(Radius) + (Slant Height)].
Volume of Cone
The V (Volume) of a cone is V = (1/3) × π × (Radius)2 × (Height).
SAT Math Formula sheet : Spheres
A sphere is the set of all points in space equidistant from a given point called the center.
Surface Area of Cone
The SA (Surface Area) of a sphere is SA = 4 × π × (Radius)2
Volume of Cone
The V (Volume) of a sphere is V = (4/3) × π × (Radius)3.
Download this Article as PDF
NOTE : (Practice Questions are Given on Home Page of This Website.)