Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Exam Math Test 29 Grid Ins Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Exam Math Test 29 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
p/3 + q/2 = 1
p – 3q = 1
Based on the system of equations above, what is the value of p?
Show/Hide Answer Key
Correct Answer: 2.33
Get rid of the fractions in the first equation by multiplying the entire equation by 6, to get 2p + 3q = 6. Whenever there are two equations with the same two variables, they can be solved simultaneously by adding or subtracting them. The key is to get one variable to disappear. Stack the equations and add them.
2p + 3q = 6
p – 3q = 1
3p = 7
Therefore, p = 7/3.
SAT Math Practice Online Test Question No 2:
3h – j = 7
2h + 3j = 1
Based on the system of equations above, what is the value of h?
Show/Hide Answer Key
Correct Answer: 2
Whenever there are two equations with the same two variables, they can be solved simultaneously by adding or subtracting equations. The key is to get one variable to cancel out. Multiply the first equation by 3 to get 9 h – 3 j = 21. Stack the equations and add them.
9h – 3j = 21
2h + 3j = 1
11h = 22
Therefore h = 2, and the correct answer is 2.
SAT Math Practice Online Test Question No 3:
If 6e(e + 3) = 3e(2e + 4) + 5, what is the value of e?
Show/Hide Answer Key
Correct Answer: 5/6
Distribute the 6e on the left side of the equation and the 3e on the right side of the equation to get 6e2 + 18e = 6e2 + 12e + 5. Subtract 6e2 from both sides of the equation to get 18e = 12e + 5. Solve for e to get 6e = 5, so e = 5/6.
The correct answer is 5/6.
SAT Math Practice Online Test Question No 4:
a+ 3b = −10
a + b= −2
In the system of equations above, what is the value of a?
Show/Hide Answer Key
Correct Answer: 2
To find a, you want to find a way to clear the b terms from the system of equations. The coefficients on the b terms are 3 and 1, so you can multiply the second equation by −3 and add the equations together. Multiplying the second equation by −3 gives you −3a – 3b = 6. Stack the equations and add:
a + 3b = -10
+(-3a – 3b = 6)
-2a = -4
Divide both sides by −2 and you find that a = 2.
SAT Math Practice Online Test Question No 5:
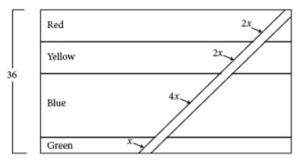
Tony has created his team flag by joining four colored rectangles, red, yellow, blue, and green, as shown in the figure above. He then added a white stripe that runs from one corner of the flag to the opposite base. If the flag has a total height of 36 inches, what is the height, in inches, of the blue rectangle?
Show/Hide Answer Key
Correct Answer: 16
Because the flag is made up of rectangles and is itself a rectangle, and the white stripe transects each rectangle at the same angle, you can use similar triangles to find the height of the blue rectangle. The total length of the white stripe is x + 4x + 2x + 2x + 9x. The triangle made by the white stripe and the blue rectangle has a white stripe distance of 4 x.
The height of this triangle is proportional to the height of the whole flag: 4x/9x = y/36, where y is the height of the triangle formed by the white stripe crossing the blue rectangle.
Solve for y by first canceling the x terms: 4/9 = y/36. Next, cross-multiply and divide and you get 9 y = (4)(36) and then y = 16. The height of the blue triangle is 16.
SAT Math Practice Online Test Question No 6:
If one angle of a right triangle measures a°, and the cos a° = 3/5, then what is sin (90 – a )°?
Show/Hide Answer Key
Correct Answer: 0.6
This question is testing your knowledge of the relationship between sine and cosine of complementary angles. This relationship is often expressed as sin x° = cos (90 – x)°. The important part of the relationship is that if the angles add up to 90°, then the sine and cosine are equal. Here, a° + (90 – a )° = 90°, so the two angles are complementary.
The cosine of one angle is equal to the sine of the other angle, so if cos a° = 3/5, then sin (90 – a°) = 3/5.
SAT Math Practice Online Test Question No 7:
12x + 3y = 90
ax + by = 15
In the system of equations above, a and b are constants. If the system has no solutions, what is the value of b/a?
Show/Hide Answer Key
Correct Answer: 0.25
If the system of equations has no solutions, then the lines described by the equations never intersect. In other words, the lines are parallel and have the same slope. The equations are in standard form: Ax + By = C . Slope in standard form is -A/B. The slope of the first equation is therefore -12/3 = -4. The second equation has the same slope, so -a/b = -4.
The question wants b/a, so you need to do some manipulation.
First, multiply both sides by −1: a/b = 4. Multiply both sides by b: a = 4 b.
Divide both sides by a: 1 = 4b/a. Divide both sides by 4 and you get 1/4 = b/a.
SAT Math Practice Online Test Question No 8:
If x = 2√5 and 4x = √5y, what is the value of y?
Show/Hide Answer Key
Correct Answer: 64
You have a system of equations and the question wants the value of y, so you want to make the x terms go away. One way to approach this is to make the x portions of the two equations equal to one another and then put the other parts of the equations equal to each other. Multiply the first equation by 4 to get 4x = 8√5.
Both equations are now equal to 4x, so you can put the other parts of the equations equal to each other: 8√5 = √5y.
Isolate y. Start by squaring both sides (don’t forget to square the 8 on the left side): 64(5) = 5 y. Divide both sides by 5 and get 64 = y.
SAT Math Practice Online Test Question No 9:
Hayoung is competing in a triathlon comprised of swimming, running, and biking. She starts by swimming m miles. Next, she runs 11 times the distance that she swims. Finally, she bikes 18 times the distance that she swims. If Hayoung swims 2.5 miles, what is the total distance in miles Hayoung travels as she competes?
Show/Hide Answer Key
Correct Answer: 75
Hayoung swims 2.5 miles. She runs 11 × 2.5 = 27.5 miles and bikes 18 × 2.5 = 45 miles. Her total triathlon mileage = 2.5 + 27.5 + 45 = 75 miles. The correct answer is 75.
SAT Math Practice Online Test Question No 10:
At the local mall, Casey’s Card Cart sells cards à la carte. Casey’s revenue R , in dollars, for x days is given by the function R (x) = 250x – 20. If Casey earned $1,230, how many days has she sold cards?
Show/Hide Answer Key
Correct Answer: 5
Plug 1,230 in for the value of the function to get 1,230 = 250 x – 20. Solve for x to get 1,250 = 250 x and x = 5. The correct answer is 5.



