Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Practice Test 28 Grid Ins Questions with Answer Keys | SAT Online Classes AMBiPi.
SAT 2022 Math Practice Test 28 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
A rectangular block with a volume of 250 cubic inches is sliced into two cubes of equal volume. How much greater, in square inches, is the combined surface area of the two cubes than the surface area of the original rectangular block?
Show/Hide Answer Key
Correct Answer: 50
If the two newly formed cubes are identical in volume, that means they must each have a volume of 250/2 = 125 cubic inches. The length of one of the cube’s edges is therefore ∛125 inches, which is equal to 5 inches. You can thus conclude that each face of the cubes is 52, or 25 square inches. Recall that two new faces were formed, so the two cubes combined will have 25 × 2 = 50 square inches more surface area than the original solid.
SAT Math Practice Online Test Question No 2:
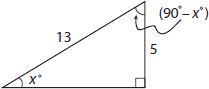
In a right triangle, one angle measures x°, where sin x° = 5/13. What is cos(90° – x°)?
Show/Hide Answer Key
Correct Answer: 5/13
Getting to the Answer: By the relationship given above, because sin x° = 5/13, cos(90° – x°) must equal the same thing, so grid in 5/13.
Note: If you didn’t know the property, you could also sketch a triangle and fill it in using SOH CAH TOA. Sine equals opp/hyp, so label one angle x, the side opposite that angle 5, and the hypotenuse 13. The third angle in the triangle must be (90° – x°) because the angles must sum to 180°.
Using SOH CAH TOA again: cos(90° – x°) = adj/hyp
cos(90° – x°) = 5/13
SAT Math Practice Online Test Question No 3:
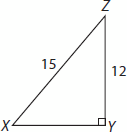
In triangle XYZ (not shown), the measure of ∠Y is 90°, YZ = 12, and XZ = 15. Triangle HJK is similar to triangle XYZ, where vertices H, J, and K correspond to vertices X, Y, and Z, respectively, and each side of triangle HJK is 1/5 the length of the corresponding side of triangle XYZ. What is the value of tan K?
Show/Hide Answer Key
Correct Answer: 3/4 or .75
Trigonometric functions are ratios. This means that it doesn’t matter whether x is an angle in a huge triangle or in a small one; tan x will always be the same. In this question, triangles XYZ and HJK are similar, which means that their corresponding angles are equal. The question asks for the tangent of K, which is the same as the tangent of Z (since Z and K are corresponding and thus congruent). Don’t bother drawing HJK and finding 1/5 of all side lengths, this is unnecessary. Just draw XYZ and find tan Z:
This is a multiple of a 3:4:5 triangle, specifically a 9:12:15 triangle (which makes the missing side 9), so z = opp/adj = 9/12 = 3/4 = 0.75.
SAT Math Practice Online Test Question No 4:
1 < (c – 1)2 < 36
What is the greatest integer solution to the inequality above?
Show/Hide Answer Key
Correct Answer: 6
Try Plugging In different values of c to see which ones work. Make a table to keep track of all the numbers.
The largest value of c that works without hitting the boundaries of the inequality is 6, so the correct answer is 6.
SAT Math Practice Online Test Question No 5:
Which h(t) = (1/2)at2
As a space probe descends to the surface of Mars, its distance in meters above the surface can be modeled by the equation above. If t is the time in seconds it will take the probe to reach the surface, and it takes the probe 8 seconds to descend the final 120 meters to the surface, what is the value of the deceleration constant a?
Show/Hide Answer Key
Correct Answer: 3.75
According to the question, h ( t ) = 120 and t = 8. Plug these values into the function to get 120 = (1/2) a (8).
Simplify the equation to get 120 = (1/2) a (64) and 120 = 32 a. Solve for a to get a = 3.75. The correct answer is 3.75.
SAT Math Practice Online Test Question No 6:
A rectangular box has a volume of 24. If the length is halved and the height is tripled, what will be the new volume of the box?
Show/Hide Answer Key
Correct Answer: 36
Plug In. Pick any values for the length, width, and height that will give you a volume of 24. If you say the length is 2, the height is 3, and the width is 4, then the new length, height, and width will be 1, 9, and 4 respectively. The new volume is 36. No matter what numbers you set for the initial length, width, and height, you will always get 36 for the new volume.
SAT Math Practice Online Test Question No 7:
If x > 0 and x2 – 25 = 0, what is the value of x ?
Show/Hide Answer Key
Correct Answer: 5
Isolate x by first adding 25 to both sides of the equation to get x2 = 25. Next, take the square root of both sides to get x = ± 5. Because the question indicates that x > 0, x must equal the positive value 5.
SAT Math Practice Online Test Question No 8:
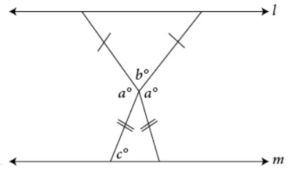
In the figure above, lines l and m are parallel, 180 – 2c = b , and c = 65. What is the value of a?
Show/Hide Answer Key
Correct Answer: 130
Start by labeling the angle with measure c as 65. Because two sides of the triangle are equal, you also know that the other angle adjacent to line m is also equal to 65. Because these angles are part of a triangle, and all triangles have 180°, the measure of the remaining angle is 180 – 65 – 65 = 50; label that as well. To find b , use the equation given; if c = 65, then 180 – 2(65) = b , so 180 – 130 = 50 = b ; label the angle with measure b as 50. Finally, to find a , you know that the full circle around the middle of the two triangles is 360°, so 50 + 50 + a + a = 360, or 100 + 2 a = 360. Subtract 100 from both sides: 2 a = 260. Divide both sides by 2, and you get a = 130.
SAT Math Practice Online Test Question No 9:
2x + 8y = 74
3x – 4y = 43
If (x , y) is the solution to the system of equations shown above, then what is the value of y?
Show/Hide Answer Key
Correct Answer: 4.25
There are many ways to isolate y in this question. One of the more straightforward ways is to actually find x first by clearing the y terms. The coefficients on y are 8 and −4, so if you multiply the second equation by 2 and add the two equations together, the y terms cancel. Multiplying the second equation by 2 gives you 6 x – 8 y = 86; stack this with the first equation and add:
[2x + 8y= 74] + [6x – 8y = 86]
8x = 160
Divide both sides by 8 to find that x = 20. Now, go back to one of the original equations to find y . In the first equation, make x = 20: 2(20) + 8 y = 74; 40 + 8 y = 74. Isolate y by first subtracting 40 from both sides: 8 y = 34. Next, divide both sides by 8: y = 34/8, or 4.25. The fraction will fit into the Grid-In boxes, so you don’t need to simplify.
SAT Math Practice Online Test Question No 10:
At a dessert shop, each cupcake has 60 more grams of sugar than each frozen yogurt. If 3 cupcakes and 4 frozen yogurts have a total of 390 grams of sugar, how many grams of sugar does each cupcake have?
Show/Hide Answer Key
Correct Answer: 90
Make c the grams of sugar in a cupcake and f the grams of sugar in a frozen yogurt. If each cupcake has 60 more grams of sugar than each frozen yogurt, then c = 60 + f . If 3 cupcakes and 4 frozen yogurts have 390 grams of sugar, then 3 c + 4 f = 390. You want to find the grams of sugar in each cupcake. To solve for c , you have a few options. One is to first solve the first equation in terms of f by subtracting 60 from each side: c – 60 = f . Next, substitute c – 60 for f in the second equation: 3 c + 4( c – 60) = 390. Next, distribute 4: 3c + 4c – 240 = 390. Combine like terms: 7c – 240 = 390. Add 240 to both sides: 7 c = 630. Divide both sides by 7, and you get c = 90.