Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Practice Exam Math Test 18 Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Practice Exam Math Test 18 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
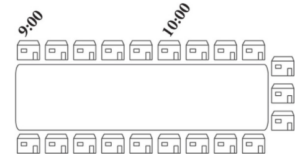
Daniel works for a pest control company and is spraying all the lawns in a neighborhood. The figure above shows the layout of the neighborhood and the times that Daniel started spraying the lawns at two of the houses. Each lawn in the neighborhood is approximately 0.2 acres in size and takes the same amount of time to spray.
Daniel uses a mobile spray rig that holds 20 gallons of liquid. It takes 1 gallon to spray 2,500 square feet of lawn. How many times, including the first time, will Daniel need to fill the spray rig, assuming he fills it to the very top each time? [1 acre = 43,560 square feet]
Show/Hide Answer Key
Correct Answer: 4
The total acreage of all the lawns in the neighborhood is 21 × 0.2 = 4.2 acres. This is equivalent to 4.2 × 43,560 = 182,952 square feet. Each gallon of spray covers 2,500 square feet so divide to find that Daniel needs 182,952 ÷ 2,500 = 73.1808 gallons to spray all the lawns. The spray rig holds 20 gallons, so Daniel will need to fill it 4 times. After he fills it the fourth time and finishes all the lawns, there will be some spray leftover.
SAT Math Practice Online Test Question No 2:
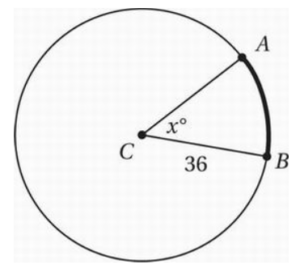
In the circle above, arc AB has a measure of 7π. What is the value of x?
Show/Hide Answer Key
Correct Answer: 35
Since an arc is simply a portion of a circumference, let’s first calculate the circumference of the circle: C = 2πr = 2π(36) = 72π
Because arc AB has a measure of 7π, it is 7π/72π = 7/72 of the entire circumference. Since x° is the measure of the central angle that corresponds to this arc, it must be the same fraction of the whole: x°/360° = 7/72
Cross multiply: 72x = 7(360)
Divide by 72: x = 7(5)
Simplify: x = 35
SAT Math Practice Online Test Question No 3:
If (2/3)a + (1/2)b = 5 and b = 4, what is the value of a?
Show/Hide Answer Key
Correct Answer: 4.5 or 9/2
Original equation: (2/3)a + (1/2)b = 5
Substitute b = 4: (2/3)a + (1/2)(4) = 5
Simplify: (2/3)a + 2 = 5
Subtract 2: (2/3)a = 3
Multiply by 3/2: a = 9/2
SAT Math Practice Online Test Question No 4:
What is one possible solution to the equation 6/(x + 1) – 3/(x – 1) = 1/4?
Show/Hide Answer Key
Correct Answer: 5 or 7
Original equation: 6/(x + 1) – 3/(x – 1) = 1/4
Multiply by 4(x + 1)(x – 1):
24(x + 1)(x – 1)/(x + 1) – 12(x + 1)(x – 1)/(x – 1) = 4(x + 1)(x – 1)/4
We do this because 4(x + 1)(x – 1) is the least common multiple of the denominators, so multiplying both sides by this will eliminate the denominators and simplify the equation.
Cancel common factors: 24(x – 1) – 12(x + 1) = (x + 1)(x – 1)
Distribute and FOIL: (24x – 24) – (12x + 12) = x2 – 1
Collect like terms: 12x – 36 = x2 – 1
Subtract 12x and add 36: 0 = x2 – 12x + 35
Factor: 0 = (x – 5)(x – 7)
Solve using Zero Product Property: x = 5 or 7
SAT Math Practice Online Test Question No 5:
If 3 – 1/b = 3/2, what is the value of b?
Show/Hide Answer Key
Correct Answer: 2/3 or.666 or. 667
3 – 1/b = 3/2
Multiply by the common denominator, 2b: 6b – 2 = 3b
Add 2: 6b = 3b + 2
Subtract 3b: 3b = 2
Divide by 3: b = 2/3
SAT Math Practice Online Test Question No 6:
The function f is a quadratic function with zeros at x = 1 and x = 5. The graph of y = f(x) in the xy-plane is a parabola with a vertex at (3, -2). What is the y-intercept of this graph?
Show/Hide Answer Key
Correct Answer: 2.5 or 5/2
We know that if a quadratic has zeroes at x = 1 and x = 5, it must have factors of (x – 1) and (x – 5). Since a quadratic can only have two linear factors, f must be of the form f(x) = k(x – 1)(x – 5).
Substitute x = 3 and y = -2 for the coordinates of vertex: -2 = k(3 – 1)(3 – 5)
Simplify: 2 = k(2)(-2)
Simplify: -2 = -4k
Divide by -4: 1/2 = k
Therefore the equation of the function is f(x) = 1/2(x – 1)(x – 5), and we can find its y-intercept by substituting x = 0:
f(0) = 1/2(0 – 1)(0 – 5)
Simplify: f(0) = 5/2
SAT Math Practice Online Test Question No 7:
If a = 4√2 and 2a =√2b, what is the value of b?
Show/Hide Answer Key
Correct Answer: 64
Given: a = 4√2
Multiply by 2: 2a = 8√2
Substitute: 2a = 2a = √2b
Square both sides: 2b = 64(2)
Divide by 2: b = 64
SAT Math Practice Online Test Question No 8:
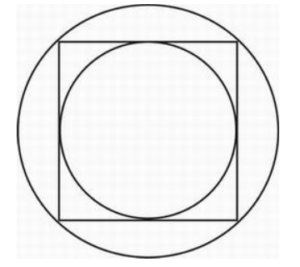
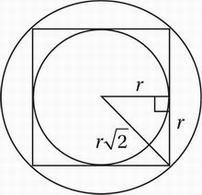
In the figure above, a circle is inscribed in a square that is inscribed in a larger circle. If the area of the larger circle is 16.5 square units, what is the area of the smaller circle?
Show/Hide Answer Key
Correct Answer: 8.25
Most students will begin this problem by trying to find the length of the radius of the larger circle. This is a bit of a pain and, as it turns out, completely unnecessary. Instead, start by drawing in the 45°-45°-90° triangle as shown, and notice that one leg of this triangle is the radius of the smaller circle, and the hypotenuse is the radius of the larger circle. This is the key to the relationship between the circles.
If we label the smaller leg r and use either the Pythagorean Theorem or the Reference Information about 45°-45°-90° triangles given at the beginning of the test, we find that the hypotenuse is r√2. Therefore, the area of the smaller circle is πr2 and the area of the larger circle is π(r√2)2 = (2πr)2.
In other words, the larger circle has an area that is twice the area of the smaller circle. Therefore, if the larger circle has area 16.5, the smaller circle has an area of 16.5 ÷ 2 = 8.25.
SAT Math Practice Online Test Question No 9:
If x2 + 12x = 13, and x < 0, what is the value of x2?
Show/Hide Answer Key
Correct Answer: 169
x2 = 12x = 13
Subtract 13: x2 + 12x – 13 = 0
Factor: (x + 13)(x – 1) = 0
Use the Zero Product Property: x = -13 or x = 1
If x < 0, x must be -13. Therefore x2 = (-13)2 = 169.
Alternately, if you have QUADFORM (a quadratic formula program) programmed into your calculator, select PROGRAM, QUADFORM, and input a = 1, b = 12 and c = -13 to find the zeros (-13 and 1).
SAT Math Practice Online Test Question No 10:
If m and n are integers such that m2 + n2 = 40 and m < 0 < n, what is the value of (m + n)2?
Show/Hide Answer Key
Correct Answer: 16
Because m2 + n2 = 40, where m and n are both integers, we must look for two perfect squares that have a sum of 40. The perfect squares are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 … and the only two of these with a sum of 40 are 4 and 36. So either m2 = 4 and n2 = 36 or m2 = 36 and n2 = 4.
CASE 1: m2 = 4 and n2 = 36
Take square root: m = ±2 and n = ±6
Since m < 0 < n: m = -2 and n = 6
Evaluate (m + n)2: (m + n)2 = (-2 + 6)2 = 42 = 16
CASE 2: m2 = 36 and n2 = 4
Take square root: m = ±6 and n = ±2
Since m < 0 < n: m = -6 and n = 2
Evaluate (m + n)2: (m + n)2 = (-6 + 2)2 = (-4)2 = 16