Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Maths Practice Test 19 Grid Ins Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Maths Practice Test 19 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
If (2/3)x + (1/2)y = 5, what is the value of 4x + 3y?
Show/Hide Answer Key
Correct Answer: 30
Algebra (linear equations) EASY
(2/3)x + (1/2)y = 5
Multiply by 6 (the common denominator):
6[(2/3)x + (1/2)y = 5]
Distribute: (12/3)x + (6/2)y = 30
Simplify: 4x + 3y = 30
SAT Math Practice Online Test Question No 2:
(1/2)x = (-1/3)y + 1/10
6x – 4y = k
For what value of k will the system of equations above have at least one solution?
Show/Hide Answer Key
Correct Answer: 1.2
Algebra (linear systems) MEDIUM-HARD
First, we should simplify the first equation : (1/2)x = (-1/3)y + 1/10
Subtract: (1/3)y
(1/2)x – (1/3)y = 1/10
Multiply by 12: 6x – 4y = 1.2
This equation represents a line with a slope of 6/4 = 3/2. The second equation, 6x – 4y = k also represents a line with a slope 6/4 = 3/2. For this system of equations to have at least one solution, these two lines must have an intersection. How can two lines with the same slope intersect? They must be identical lines, and therefore intersect in all of their points. If this is the case, then k must equal 1.2.
SAT Math Practice Online Test Question No 3:
What is the smallest integer value of x such that (6/x) + (1/2x) is less than 1?
Show/Hide Answer Key
Correct Answer: 7
Advanced Mathematics (rational equations) EASY
Given inequality: (6/x) + (1/2x) < 1
Multiply by 2x: 12 + 1 < 2x
Simplify: 13 < 2x
Divide by 2: 6.5 < x
The smallest integer that is greater than 6.5 is 7.
SAT Math Practice Online Test Question No 4:
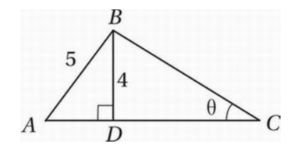
In the figure above, triangle ABC has an area of 19. What is the value of tan θ?
Show/Hide Answer Key
Correct Answer: 18
Special Topics (trigonometry) HARD 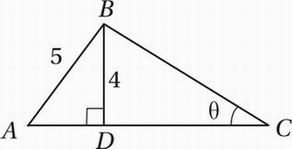
Find AD with Pythagorean Theorem: (AD)2 + 42 = 52
Simplify: (AD)2 + 16 = 25
Subtract 16: (AD)2 = 9
Take square root: AD = 3
Or, even better, just notice that triangle ADB is a 3-4-5 right triangle.
Use triangle area formula to find AC: Area = (1/2)bh = 1/2(AC)(4) = 19
Simplify: 2(AC) = 19
Divide by 2: AC = 19/2
Find DC: DC = AC – AD = 19/2 – 3 = 19/2 – 6/2 = 13/2
Find tan θ: tan θ = opp/hyp = BD/DC = 4/(13/2) = 4 x 2/13 = 8/13
SAT Math Practice Online Test Question No 5:
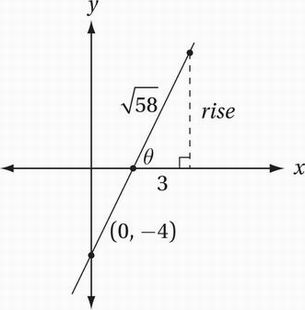
When graphed in the xy-plane, the line y = mx – 4 intersects the x-axis at an angle of θ. If m > 0, 0° < θ < 90°, and cos θ = 3/√58, what is the value of m?
Show/Hide Answer Key
Correct Answer: 7/3 or 2.33
Special Topics (trigonometry) HARD
The graph of the line y = mx – 4 has a slope of m and a y-intercept of -4. Since m > 0, this slope is positive. We are told that this line intersects the x-axis at an angle of θ, where cos θ = θ = 3/√58 This gives us enough information to sketch a fairly detailed graph:
Notice that this information lets us construct a right triangle that includes θ, in which the adjacent side has length 3 and the hypotenuse has length√58 (remember cos θ = adjacent/hypotenuse). This triangle is particularly handy because it depicts the rise and the run for a portion of the line, which will enable us to find the slope. We simply have to find the rise with the Pythagorean Theorem: 32 + rise2 = (√58)2
Simplify: 9 + rise2 = 58
Subtract 9: rise2 = 49
Take square root: rise = 7
Therefore, the slope of the line is m = rise/run = 7/3.
SAT Math Practice Online Test Question No 6:
x + 36/x = 12
If x > 0, what is the solution to the equation above?
Show/Hide Answer Key
Correct Answer: 6
Advanced Mathematics (quadratic equations) HARD
Although this does not look like a quadratic equation, in fact, it is.
Original equation: x + 36/x = 12
Multiply by x: x2 + 36 = 12x
Subtract 12x: x2 – 12x + 36 = 0
Factor: (x – 6)(x – 6) = 0
Solve using the Zero Product Property: x – 6 = 0, so x = 6
SAT Math Practice Online Test Question No 7:
If y varies inversely as x, and y = ½ when x = 10, then for what value of x does y = 25?
Show/Hide Answer Key
Correct Answer: 1/5 or 0.2
Data Analysis (variation) MEDIUM
If y varies inversely as x: y = k/x
Substitute ½ = y and 10 = x: 1/2 = k/10
Cross multiply: 10 = 2k
Divide by 2: 5 = k
Therefore the general equation is: y = 5/x
Substitute 25 = y: 25 = 5/x
Multiply by x: 25x = 5
Divide by 25: x = 5/25 = 1/5
SAT Math Practice Online Test Question No 8:
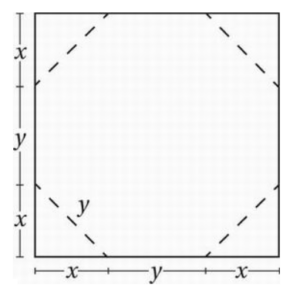
Four triangles are to be cut and removed from a square piece of sheet metal to create an octagonal sign with eight equal sides, as shown in the figure above. If the total area of the removed material is 196 square centimeters, what is the perimeter, in centimeters, of the octagon?
Show/Hide Answer Key
Correct Answer: 112
Special Topics (polygons) MEDIUM-HARD
Notice that the “cutouts” can be reassembled to form two squares with side x and diagonal y, leaving an octagon with a perimeter of 8y.
Since each of the cutout triangles is a right triangle: x2 + x2 = y2
Simplify: 2x2 = y2
If the total area of the “cutouts” is 196 square centimeters: 2x2 = 196
Substitute 2x2 = y2: y2 = 196
Take square root: y = 14
Therefore the perimeter of the octagon is 8 × 14 = 112.
SAT Math Practice Online Test Question No 9:
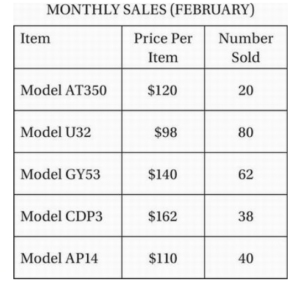
The table above shows information about the February sales for five different cell phone models at a local store. What was the median price, to the nearest dollar, of the 240 phones sold in February?
Show/Hide Answer Key
Correct Answer: 115
Data Analysis (central tendency) MEDIUM
Begin by putting the data in order from least expensive to most expensive:
80 phones sold for $98
40 phones sold for $110
20 phones sold for $120
62 phones sold for $140
38 phones sold for $162
We don’t have to actually write out the prices of all 240 phones to find the median price. We can divide any set of 240 numbers, in ascending order, into two sets of 120 numbers. The median is in the middle of these, so it is the average of the 120th and 121st numbers. Since the first two categories account for 40 + 80 = 120 of these numbers, the 120th number in the set is $110, and the 121st number in the set is in the next higher category, $120. The median price is therefore ($110 + $120)/2 = $115.
SAT Math Practice Online Test Question No 10:
Performance Banner Company creates promotional banners that include company logos. The Zypz Running Shoe Company would like a 4-foot high and 20-foot long banner that includes its logo, which has a height-to-length ratio of 5:8.
Performance Banner Company charges its customers $1.20 per square foot for the banner material, $2.50 per square foot of any printed logo, and $32 in fixed costs per banner. The Zypz Running Shoe Company is considering two options for the banner: one with a single logo, and another with two logos. If these logos are all to be the same size as described in Part 1, what percent of the banner costs would the company save by choosing the single-logo option instead of the two-logo option? (Ignore the % symbol when entering into the grid. For example, enter 27% as 27.)
Show/Hide Answer Key
Correct Answer: 25
Problem Solving (extended thinking) HARD
The banner has dimensions of 20 feet by 4 feet, so its area is 20 × 4 = 80 square feet. If the company charges $1.20 per square foot for the banner material, this cost is 80 × $1.20= $96. Based on the logo dimensions we determined in the previous problem, the area of the logo is 4 × 6.4 = 25.6 square feet. If the company charges $2.50 per square foot for the logo, the cost per printed logo is 25.6 × $2.50 = $64.
If the company charges a fixed cost of $32 per banner, then the total cost of a banner with ONE logo would be $96 + $64 + $32 = $192. The total cost of a banner with TWO logos would be $96 + $64 + $64 + $32 = $256.
We can calculate the percent savings with the “percent change” formula since we are considering a “change” from the more expensive banner to the less expensive banner. 192 – 256/256 x 100% = -64/256 x 100% = -25%
Therefore the percent savings is 25(%).