Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Practice Exam Math Test 43 Grid Ins Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Practice Exam Math Test 43 Multiple Choice Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
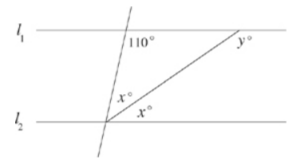
If l1 is parallel to l2 in the figure above, what is the value of y?
Show/Hide Answer Key
Correct Answer: 145
Because the two lines are parallel, 110 + 2x = 180. Solving this equation for x, you get x = 35.
Looking at the triangle, the missing angle (m) can be found by solving the equation 110 + x + m = 180. If x = 35, m = 35. If m + y = 180 and m = 35, y = 145.
SAT Math Practice Online Test Question No 2:
AB is perpendicular to BD and AB and CD bisect each other at point X. If AB = 8 and CD = 10, what is the length of BD?
Show/Hide Answer Key
Correct Answer: 3
The first step is to draw a diagram:
You should notice that BD is part of one of ETS’s favorite right triangles: a 3:4:5 triangle. So BD = 3.
SAT Math Practice Online Test Question No 3:
If ab = 4, and 3b = 2, what is the value of a?
Show/Hide Answer Key
Correct Answer: 8
Using 3b = 2, solve for b by dividing both sides by 3 to get b = 2/3. That means a2/3 = 4.
Fractional exponents tell you to use the denominator as the root and use the numerator as a regular exponent. So, ∛a2 = 4.
First, cube both sides to find a2 = 43 = 64. Next, take the square root of both sides to find a = 8.
SAT Math Practice Online Test Question No 4:
The Tyler Jackson Dance Company plans to perform a piece that requires 2 dancers. If there are 7 dancers in the company, how many possible pairs of dancers could perform the piece?
Show/Hide Answer Key
Correct Answer: 21
Let’s say you have seven dancers: A, B, C, D, E, F, and G. How many different ways can you pair them up?
This is a combination question, because A and B are the same pair as B and A, and you don’t want to count them twice. Start by finding the number of possible permutations: 7 × 6 = 42.
Finally, divide this number by 2 × 1 = 2 (we’re looking to fill 2 positions) to eliminate redundant combinations. There are 21 possible combinations.
SAT Math Practice Online Test Question No 5:
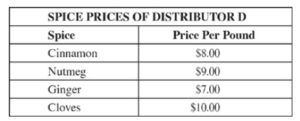
The owner of a spice store buys 3 pounds each of cinnamon, nutmeg, ginger, and cloves from distributor D. She then sells all of the spices at $2.00 per ounce. What is her total dollar profit (1 pound = 16 ounces)? (Disregard the $ sign when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 282
This is a hard question, so you have to stay on your toes. If the owner buys 3 pounds of each spice, that means she pays the following amounts for each spice:
cinnamon: $8 x 3 = $24
nutmeg: $9 x 3 = $27
ginger: $7 x 3 = $21
cloves: $10 x 3 = $30
So she pays a total of 24 + 27 + 21 + 30, or $102 for 12 pounds of spices. She then sells the spices per ounce, so you have to figure out first how many ounces of spices she has.
If 1 pound is 16 ounces, then 12 pounds is 12 × 16, or 192 ounces. She sells all the spices at $2 per ounce, so she makes 192 × $2, or $384.
To figure out her profit, subtract the amount she paid for the spices from the amount she made selling them: $384 – $102 = $282.
SAT Math Practice Online Test Question No 6:
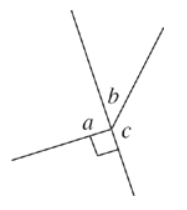
In the figure above, what is the value of a + b + c?
Show/Hide Answer Key
Correct Answer: 270
The trick here is that ETS is not asking for the value of a, b, or c.
It just wants to know what they add up to. ETS is testing only the Rule of 360.
All the angles in the figure make up a circle, so they all add up to 360. The right angle is 90 degrees, so 90 + a + b + c = 360.
Therefore a + b + c = 270.
SAT Math Practice Online Test Question No 7:
If 4x + 2y = 24 and 7y/2x = 7, what is the value of x?
Show/Hide Answer Key
Correct Answer: 3
You can solve this question using simultaneous equations because you have two equations with two variables.
First, you need to rearrange the equations a bit: 4x + 2y = 24 divided by 2 on both sides becomes 2x + y = 12.
7y/2x = 7, multiplied by 2x on both sides, becomes 7y = 14x. This, divided by 7 on both sides, becomes y = 2x, which can be manipulated into 2x – y = 0.
Now you can add the equations:
2x + y = 12
2x – y = 0
4x = 12
So x = 3.
SAT Math Practice Online Test Question No 8:
The American Ballet Repertory Company will choose 4 new corps members from its apprentice program. The apprentice program is made up of 6 women and 6 men. If 3 women and 1 man are to be chosen for the corps, how many different groupings are possible?
Show/Hide Answer Key
Correct Answer: 120
There are a total of 6 women to choose from and the company needs 3, so you would calculate 6 × 5 × 4 = 120.
However, because the order doesn’t matter, we need to get rid of duplicates.
Mathematically this is done by dividing your answer by the factorial of the number of spaces you need to fill. Because we need 3, we divide by 3! or 6, which leaves us with 20.
Now, on to the men. There are 6 men to choose from and we need only 1. So there are 6 ways to choose that. Now we have to count our women (20) and our men (6).
Remember in the probability that and means multiply. 20 × 6 = 120, which is the answer.
SAT Math Practice Online Test Question No 9:
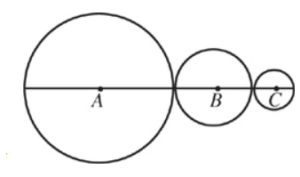
In the figure above, the radius of the circle with center A is twice the radius of the circle with center B and four times the radius of the circle with center C. If the sum of the areas of the three circles is 84π, what is the length of AC?
Show/Hide Answer Key
Correct Answer: 18
To answer this question you have to set up an equation.
If the radius of C is r, then the radius of B is 2r and the radius of A is 4r. The formula for the area of a circle is πr2.
Because 84π is the sum of the areas of the circles, this is your equation:
πr2 + π(2r)2 + π(4r)2 = 84π
r2 + 4r2 + 16r2 = 84
21r2 = 84
r2 = 4
r = 2
If r = 2, then the radius of C is 2, the radius of B is 4, and the radius of A is 8.
AC consists of the radius of A, the diameter of B, and the radius of C, so AC = 8 + 4 + 4 + 2 = 18.
SAT Math Practice Online Test Question No 10:
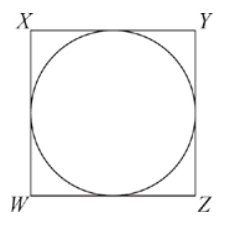
In the figure above, a circle is inscribed in square WXYZ. If the area of the circle is 400π, what is the area of WXYZ?
Show/Hide Answer Key
Correct Answer: 1600
If the area of the circle is 400π, then you can figure out its radius. A = πr2 so 400 = πr2, and the radius is 20.
The diameter of the circle is twice the radius, or 40.
Because this circle is inscribed in the square, you know that the diameter of the circle is equal to one side of the square, so you know that each side is equal to 40. The area of the square is 40 × 40 = 1,600.