Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Practice Problems Test 42 Grid Ins Math Questions with Answer Keys | SAT Online Classes AMBiPi.
SAT 2022 Practice Problems Test 42 Grid Ins Math Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
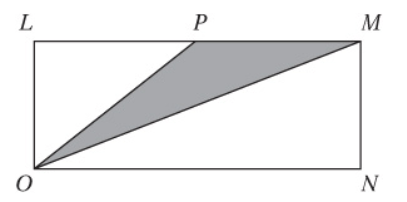
In rectangle LMNO above, P is the midpoint of side LM. If the perimeter of the rectangle is 48 and side LM is twice the length of side LO, what is the area of the shaded region?
Show/Hide Answer Key
Correct Answer: 32
Let LM = x, and let LO = y,
Since x is twice the length of y, x = 2y.
x + x + y + y = P
Substitute for x: 2y + 2y + y + y = P
Combine terms: 6y = P
Plug in 48 for P: 6y = 48
Divide by 6: y = 8
Solve for x: x = 2y = 2(8) = 16
To find the area of the shaded region, you might notice that if PM is the base of the shaded triangle, then LO is the height, so area = 1/2(base)(height) = 1/2(8)(8) = 32.
If you don’t notice this, you can find the shaded area by finding the area of the rectangle and subtracting the areas of the two unshaded triangles.
Area of rectangle = (length)(width) Area of rectangle = (x)(y) = (16)(8) = 128
Area of triangle PLO = 1/2(base)(height)
Area of triangle PLO = 1/2(8)(8) = 32
Area of triangle MNO = 1/2(base)(height)
Area of triangle MNO = 1/2(16)(8) = 64
Area of triangle OPM = 128 – 64 – 32 = 32
SAT Math Practice Online Test Question No 2:
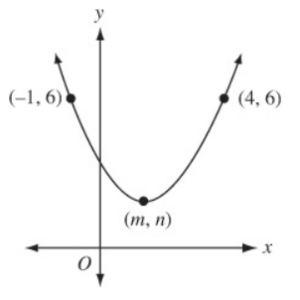
The figure above shows the graph in the xy-plane of a quadratic function with a vertex at (m, n). What is the value of m?
Show/Hide Answer Key
Correct Answer: 1.5
Since the graph is a parabola, it has a vertical axis of symmetry through the vertex. The points (-1, 6) and (4, 6) have the same y-coordinate, so each one is the reflection of the other over the axis of symmetry.
This axis, therefore, must be halfway between the two points. Since the average of -1 and 4 is (-1 + 4)/2 = 1.5, the axis symmetry must be the line x = 1.5, and therefore m = 1.5.
SAT Math Practice Online Test Question No 3:
A jar contains only black, white, and red marbles. If randomly choosing a black marble is four times as likely as randomly choosing a white marble, and randomly choosing a red marble is five times as likely as randomly choosing a black marble, then what is the smallest possible number of marbles in the jar?
Show/Hide Answer Key
Correct Answer: 25
Let b = the number of black marbles, w = the number of white marbles, and r = the number of red marbles in the jar. If you are four times as likely to choose a black marble as a white one, then b = 4w.
If you are five times as likely to choose a red marble as a black one, then r = 5b.
To find the least possible number of marbles in the jar, imagine you have only one white marble. This would mean you have 4(1) = 4 black marbles and 5(4) = 20 red marbles, for a total of 1 + 4 + 20 = 25 marbles.
In general, you can represent the total number of marbles as total = b + w + r
Since r = 5b: total = b + w + 5b
Since b = 4w: total = 4w + w + 5(4w)
Simplify: total = 4w + w + 20w
Simplify: total = 25
In other words, the number of marbles in the jar must be a multiple of 25. The smallest positive multiple of 25 is, of course, 25.
SAT Math Practice Online Test Question No 4:
When n is divided by 5, the remainder is 4. When n is divided by 4, the remainder is 3. If 0 < n < 100, what is one possible value of n ?
Show/Hide Answer Key
Correct Answer: 19, 39, 59, 79, or 99
The simplest way to solve this problem would be to find values of n that satisfy the first condition and then to check which of those also satisfies the second condition. So, let’s find some numbers that leave a remainder of 4 when divided by 5: {9, 14, 19, 24, 29}.
That should be enough. Now let’s check which of these leaves a remainder of 3 when divided by 4: 9 ÷ 4 = 2R1
14 ÷ 4 = 3R2
19 ÷ 4 = 4R3
19 is one acceptable response.
SAT Math Practice Online Test Question No 5:
There are 250 students in 10th grade at Northgate High School. All 10th graders must take French or Spanish, but not both. If the ratio of males to females in 10th grade is 2 to 3, and 80 of the 100 French students are male, how many female students take Spanish?
Show/Hide Answer Key
Correct Answer: 130
First, use a Ratio Box to find the number of males and females. If the ratio is 2 to 3, the total ratio is 5. The actual is 250, so the multiplier is 50. That means there are 50 × 2 = 100 males and 50 × 3 = 150 females. Set up a group grid (the bolded numbers are information from the problem):
You find that 20 females must be taking French, and because there are 150 females in total, 130 must be taking Spanish.
SAT Math Practice Online Test Question No 6:
Hanna is arranging tools in a toolbox. She has one hammer, one wrench, one screwdriver, one tape measure, and one staple gun to place in 5 empty spots in her toolbox. If all of the tools will be placed in a spot, one tool in each spot, and the hammer and screwdriver fit only in the first 2 spots, how many different ways can she arrange the tools in the spots?
Show/Hide Answer Key
Correct Answer: 12
Start with the most restricted spots. 2 tools can go in the first spot. Once you put 1 there, only 1 tool can go in the second spot. Once you’ve used these 2 tools, there are only 3 that can go in the third spot, then 2 in the fourth spot, and 1 in the fifth spot. So, there are 2 × 1 × 3 × 2 × 1 = 12 ways to arrange the tools.
SAT Math Practice Online Test Question No 7:
A researcher found that the amount of sleep that she allowed her mice to get was inversely proportional to the number of errors the mice made, on average, in a maze test. If mice that got 2 hours of sleep made 3 errors in the maze test, how many errors, on average, do mice with 5 hours of sleep make?
Show/Hide Answer Key
Correct Answer: 1.2
Inversely proportional means x1y1 = x2y2 where x represents hours of sleep and y represents the number of errors: (2 hours)(3 errors) = (5 hours)(y errors). 6 = 5y, so y = 6/5.
SAT Math Practice Online Test Question No 8:
A rectangular box has a height of 4.5 inches and a base with an area of 18 square inches. What is the volume of the rectangular box in cubic inches?
Show/Hide Answer Key
Correct Answer: 81
The formula for the volume of a box is length × width × height. But the question gives you the area of the base of the crate, so you already know that length × width = 18. The volume of the crate, then, is simply the area of the base times the height: 18 × 4.5 = 81.
SAT Math Practice Online Test Question No 9:
If b is a prime number such that 3b > 10 > 5/6b, what is one possible value of b?
Show/Hide Answer Key
Correct Answer: 5, 7 or 11
First, think of a prime number that will make 3b greater than 10. How about 5? To see if that fits the other side of the inequality, you need to find the value of 5/6 x 5 = 25/6, which is less than 10, so 5 is one possible value of b.
Remember: You need to find only one possible value of b.
SAT Math Practice Online Test Question No 10:
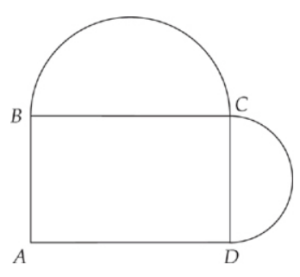
In the figure above, if semicircular arc BC has length 6π and semicircular arc CD has length 4π, what is the area of rectangle ABCD ?
Show/Hide Answer Key
Correct Answer: 96
You know that arc BC is a semicircle, which means it’s half a circle. So the circumference of the entire circle would be 6π × 2 = 12π. Therefore, the diameter of that circle is 12.
Because BC is also a side of the rectangle you know that the length of rectangle ABCD is 12. You can also use the same method to find the width.
If the length of semicircle CD is 4π, then the circumference of the entire circle would be 8π and the diameter is 8. Because CD is the width of the rectangle, you can find the area: length × width = 12 × 8 = 96.
