Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Prep Test 27 Math Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Prep Test 27 Math Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
What is the area, in square units, of an isosceles right triangle with a hypotenuse of 2?
Show/Hide Answer Key
Correct Answer: 1
The side lengths of a 45-45-90 triangle are in the ratio x: x: x√2. The length of the hypotenuse is given as 2, so x√2 2, and consequently x = 2/√2, which is the length of each leg (or in a right triangle, the base, and the height). Substitute this value into the area formula for b and h to find that A = (1/2)bh = 1/2(2/√2)(2/√2) = 4/4 = 1
SAT Math Practice Online Test Question No 2:
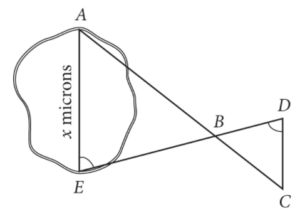
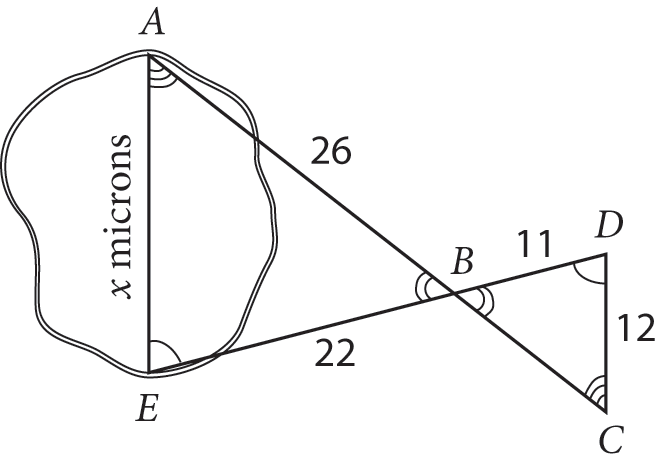
A scientist looking at a sample of infected tissue through a microscope wants to find the length x, in microns, across a damaged blood cell, as represented in the sketch above. The lengths represented by AB, EB, BD, and CD were determined to be 26 microns, 22 microns, 11 microns, and 12 microns, respectively. Given that the measure of ∠AEB is equal to the measure of ∠CDB, what is the value of x?
Show/Hide Answer Key
Correct Answer: 24
Start by filling in as much information as you can on the diagram. The given angles are already marked with a single hash mark. You also know that m∠ABE = m∠CBD because they are vertical angles, so mark this pair with double hash marks. You can reason that when two angles of a triangle are congruent to two angles of another triangle, all three pairs of angles must be congruent (because the angles of a triangle always add up to 180 degrees). Thus, m∠A = m∠C, which can be marked with triple hash marks. Then add all the known lengths. Your diagram should look like the following:
Use the hash marks to write a similarity statement-start with the angles marked with one hash mark, then two hash marks, then three: ΔEBA ~ ΔDBC. Now you can see from the order of the letters that EB and DB are corresponding sides, and one is twice the other. Thus, AE, which the question asks about, corresponds to CD, and it is twice as long. Twice 12 is 24, which is the correct answer.
SAT Math Practice Online Test Question No 3:
What is the maximum number of boxes with dimensions 2 inches by 3 inches by 4 inches that could fit in a cube-shaped container that has a volume of 1 cubic foot?
Show/Hide Answer Key
Correct Answer: 72
Before finding the volume of the cube-shaped container, convert its dimensions to inches so all the units match. The cube-shaped container has a volume of 12 × 12 × 12 cubic inches. Divide this quantity by the volume of one smaller box to get the answer: (12 x 12 x 12)/(2 x 3 x 4) = 72.
SAT Math Practice Online Test Question No 4:
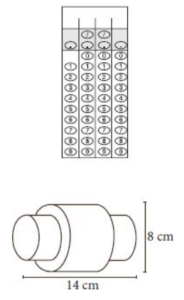
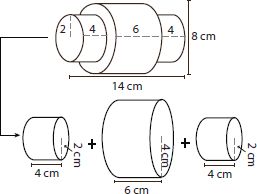
A locking pin is often made using a cylinder-cylinder pair in which a narrow cylinder fits tightly inside a wider cylinder. The inner cylinder protrudes from the outer cylinder, usually by equal amounts on both ends. In the diagram above, the radius of the inner cylinder is half the radius of the outer cylinder, and it protrudes from the outer cylinder by 4 centimeters on each end. What is the volume of the locking pin? Round your answer to the nearest cubic centimeter.
Show/Hide Answer Key
Correct Answer: 402
The three cylinders of the locking pin with their dimensions are shown below:
The volume of a cylinder is equal to πr2h, so each of the two smaller end cylinders has a volume of π x 22 x h = 16π cubic centimeters; double this to get 32π cubic centimeters for the ends. Repeat for the middle cylinder: V = π x 42 x 6 = 96π cubic centimeters. Adding the volumes together yields 32π + 96π = 128π cubic centimeters. Rounded to the nearest cubic centimeter, this value becomes 128 × 3.14 ≈ 402 cubic centimeters.
SAT Math Practice Online Test Question No 5:
The angles of a triangle are in the ratio 1:2:3. What is the sine of the smallest angle?
Show/Hide Answer Key
Correct Answer: 1/2 or .5
You’re told that the angles of the triangle are in the ratio 1:2:3. Call the smallest angle x°, the next smallest (2x)°, and the largest (3x)°. Because the angles of a triangle add to 180°: x° + (2x)° + (3x)° = 180°
(6x)° = 180°
x° = 30°
SAT Math Practice Online Test Question No 6:
y = x
(y – 2)2 – 4 = -x
The system of equations above intersects at two points. What is the sum of the coordinates of the point of intersection in Quadrant I?
Show/Hide Answer Key
Correct Answer: 6
Substitute x for y in the second equation to get ( x – 2)2 – 4 = – x. Expand the left side of the equation to get ( x – 2)( x – 2) – 4 = – x or x2 – 4 + 4 = – x . Simplify the equation to get x2 – 4 x = – x . Set the equation to 0 to get x2 – 3 x = 0. Factor an x out of the equation to get x ( x – 3) = 0. Therefore, either x = 0 or x – 3 = 0 and x = 3. According to the question, the point of intersection is in quadrant I, where the x and y values are both positive. Therefore, x = 3 and y = 3. The sum of 3 + 3 = 6. The correct answer is 6.
SAT Math Practice Online Test Question No 7:
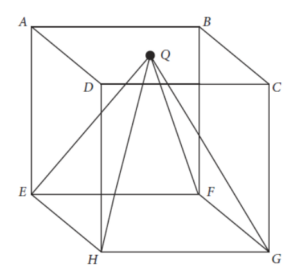
A cube with a side length of 6 is shown in the figure above. If point Q lies on square ABCD and is equidistant from points A, B, C, and D, what is the volume of pyramid EFGHQ?
Show/Hide Answer Key
Correct Answer: 72
The formula for the volume of a pyramid, given at the start of each math section, is V = (1/3)lwh, where l is the length of the base, w is the width of the base, and h is the height. Since the cube has side 6, the length and width of the base are both 6.
The height of the pyramid is also the height of the cube, which is also 6. Plug these into the formula to get V = (1/3)(6)(6)(6) = 72.
SAT Math Practice Online Test Question No 8:
3h – j = 7
2h + 3j = 1
Based on the system of equations above, what is the value of h?
Show/Hide Answer Key
Correct Answer: 2
Whenever there are two equations with the same two variables, they can be solved simultaneously by adding or subtracting equations. The key is to get one variable to cancel out. Multiply the first equation by 3 to get 9 h – 3 j = 21. Stack the equations and add them.
9h – 3j = 21
2h + 3j = 1
11h = 22
Therefore h = 2, and the correct answer is 2.
SAT Math Practice Online Test Question No 9:
Abeena is making punch for a winter party in a punch bowl that can hold at most 9 quarts. She wants to get as much vitamin C in her punch as possible, so she is using only orange juice and grape juice. She has 6 quarts of orange juice, which has 2 grams of vitamin C per quart, and 7 quarts of grape juice, which has 1 gram of vitamin C per quart. If there are 4 cups in a quart, what is the greatest possible amount of vitamin C, in grams, that Abeena can have in one cup of her punch?
Show/Hide Answer Key
Correct Answer: 416 or .417
Start by calculating the amount of vitamin C in the entire punch bowl and then calculate what the equivalent in only one cup would be. To maximize the amount of vitamin C in the punch bowl, Abeena will need to add as much orange juice, which has the highest concentration of vitamin C, as she can. Given that the punch bowl holds 9 quarts, she will pour in 6 quarts of orange juice (which is all she has) and 3 quarts of grape juice. The amount of vitamin C can be calculated as follows:
Therefore, the 9 quarts of a punch contain 15 grams of vitamin C. Next, convert the quarts to cups. Since there are 4 cups in 1 quart, 9 × 4 = 36 cups in 9 quarts. To figure out how much vitamin C is in one cup, set up the following proportion: 15 grams/36 cups = x grams/1 cup. Cross multiply to get 36 x = 15, or x = 36/15 = 5/12.
The correct answer is 5/12. Only reduce a fraction if it is necessary to make it fit in the grid-in box.
SAT Math Practice Online Test Question No 10:
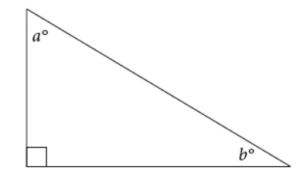
In the figure above, cos a° = 5/13. What is sinb°?
Show/Hide Answer Key
Correct Answer: .384 or .385
Remember SOHCAHTOA. cos = adjacent/hypotenuse. Therefore, the adjacent side of angle a is equal to 5, and the hypotenuse of the triangle is equal to 13. sin = opposite/hypotenuse.
The opposite side of angle b is equal to 5, and the hypotenuse of the triangle is 13. Therefore, sinb° = 5/13.
