Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Practice Test 26 Math Grid Ins Questions with Answer Keys | SAT Online Classes AMBiPi.
SAT 2022 Practice Test 26 Math Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
Comix Fanatix has 250 customers who subscribe to its newsletter, 68% of whom are male. After some female customers cancel their subscriptions, the total number of subscribers becomes 1.3 times the number of male subscribers. How many female customers canceled their subscriptions?
Show/Hide Answer Key
Correct Answer: 29
There are 250 subscribers, 68% of whom are male. That makes 250 × 0.68 = 170 male subscribers. After some females unsubscribe, the total subscriber count is 1.3 times the number of male subscribers, for a total of 170 × 1.3 = 221 subscribers. Here you have to pause and make sure you solve for the right thing: The question asks for the number of females who unsubscribed, which is 250 – 221 = 29 females.
SAT Math Practice Online Test Question No 2:

The bar graph above shows the results of a grammar quiz in a language arts class. What is the difference between the mean and median of the quiz scores? Round your answer to the nearest hundredth.
Show/Hide Answer Key
Correct Answer: .29
When data values are arranged from least to greatest, the median is the value in the middle. Add the bar heights to find that there are 52 students represented in the bar graph, which is an even number, so take the average of the two middle values to get the median. Half of 52 is 26, so the values in the middle are the 26th and 27th values. Both of these values are 6, so the median is 6. To find the mean, add all the quiz scores together and divide by the number of students, 52. To speed up the calculations, multiply each bar height by the corresponding score (mentally if possible): [(1 x 1) + (3 x 3) + (5 x 4) + (8 x 5) + (10 x 6) + (11 x 7) + (8 x 8) + (4 x 9) + (2 x 10)] ÷ 52 = 327/52 ≈ 6.2885.
Rounded to the nearest hundredth, the difference between the median and the mean is 6.29 – 6 = 0.29. Grid this in as .29.
SAT Math Practice Online Test Question No 3:
If x = 8√3 and 3x = √3y, what is the value of y?
Show/Hide Answer Key
Correct Answer: 576
First, substitute 8√3 for x into the equation and simplify. Next, write √3y as √3√y so you can divide both sides by so you can divide both sides √3. Finally, square both sides to eliminate the radical:
3x = √3y
3(8√3) = √3y
24√3 = √3y
24√3 = √3√y
24 = √y
242 = y
Squaring 24, the final answer is 576.
SAT Math Practice Online Test Question No 4:
What is one possible solution to the rational equation 1/x – 2/(x – 2) = 3?
Show/Hide Answer Key
Correct Answer: 2/3 or 1
Multiplying both sides of the equation by the common denominator (x)(x – 2) yields the following:
[x(x – 2)/1] ⦁ [1/x – 2/(x – 22) = 3]
1(x – 2) – 2(x) = 3(x) (x – 2)
x – 2 – 2x = 3(x2 – 2x)
-x – 2 = 3x2 – 6x
0 = 3x2 – 5x + 2
Now, factor the equation (or use the quadratic formula), set each factor equal to 0, solve for x, and check that the solutions don’t result in a zero denominator.
0 = 3x2 – 5x + 2
0 = (3x – 2)(x – 1)
The solutions are x = 2/3 and x = 1, both of which are valid solutions, so grid in either value.
SAT Math Practice Online Test Question No 5:
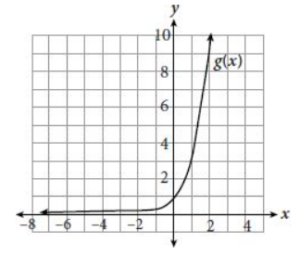
An exponential function g(x) is shown in the figure above. What is the exact value of g(–4)?
Show/Hide Answer Key
Correct Answer: 1/81
The notation g(-4) means that you are looking for the y-value when x is -4. Because you cannot tell what the exact value is from the graph, you need to find the equation of the function. To find the base, b, which is being raised to a power, make a list of several points on the graph and look for a pattern: (0, 1), (1, 3), and (2, 9). The y-values are all powers of 3, so try b = 3. Notice that 30 = 1, 31 = 3, and 32 = 9. The equation of the function is g(x) = 3x, so substitute -4 for x and simplify:
g(-4) = 3-4 = 1/3 = 1/(3 x 3 x 3 x 3) = 1/81
SAT Math Practice Online Test Question No 6:
If x = –4 when x2 + 2xr + r2 = 0, what is the value of r?
Show/Hide Answer Key
Correct Answer: 4
The equation is a special product of binomials (the square of a sum), so when factored, it becomes (x + r)2 = 0 (you could also factor normally if you didn’t recognize this). Substitute -4 for x, and then solve for r by taking the square root of both sides:
(-4 + r)2 = 0
r – 4 = 0
r = 4
SAT Math Practice Online Test Question No 7:
Two complex numbers, A and B, are defined as A = (3 – 4i) and B = (9 + ki), where k is a constant. If AB – 15 = 60, what is the value of k? (Note: i2 = -1)
Show/Hide Answer Key
Correct Answer: 12
You know that AB – 15 = 60. Solve this for AB by adding 15 to both sides of the equation: AB = 75. Next, substitute the expressions given for A and B, multiply them together, and see where that takes you:
AB = 75
(3 – 4i)(9 + ki) = 75
27 + 3ki – 36i – 4ki2 = 75
27 – 36i + 3ki – 4k(-1) = 75
27 – 36i + 3ki + 4k = 75
You now have two options: The only way the expression on the left can equal plain 75 is if the imaginary terms add up to 0, so you could set the two imaginary terms equal to 0 and solve for k:
-36i + 3ki = 0
3ki = 36i
3k = 36
k = 12
The other option is to ignore the imaginary terms (because they add up to 0) and set the real terms equal to 75 and solve for k. The result should be the same:
27 + 4k = 75
4k = 48
k = 12
Either route leads to the correct answer, which is 12.
SAT Math Practice Online Test Question No 8:
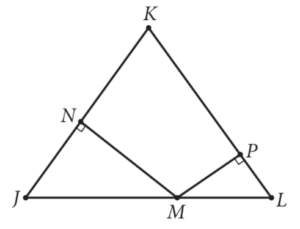
In triangle JKL above, JK = KL and JL = 26. The ratio of MN to MP is 8:5. What is the length of segment JM?
Show/Hide Answer Key
Correct Answer: 16
The given ratio involves sides of the two small right triangles, and the question asks about a side of one of those triangles, so focus on this. The base angles of ΔJKL are congruent (because it is an isosceles triangle), so ∠J and ∠L are congruent. Additionally, ∠JNM and ∠LPM are both right angles and therefore are congruent. When two pairs of corresponding angles in two triangles are congruent, the third pair must also be congruent, so ΔJNM and ΔLPM are similar by AAA. This means the corresponding sides of these triangles are proportional. Thus, JM/ML = MN/MP. Because MN/MP = 8/5, it follows that JM/ML = 8/5. If we let JM = 8x, then ML = 5x. We also know that JL (which is the sum of the lengths of segments JM and ML) equals 26, so 8x + 5x = 26. Solving this equation yields 13x = 26, or x = 2. Finally, JM = 8(2) = 16.
SAT Math Practice Online Test Question No 9:
A cube and a rectangular solid are equal in volume. If the lengths of the edges of the rectangular solid are 4, 8, and 16, what is the length of an edge of the cube?
Show/Hide Answer Key
Correct Answer: 8
The volume of the rectangular solid is 4 × 8 × 16 = 512 cubic units. The cube has the same volume, and its edges are all equal in length, so express this as s3 = 512 and take the cube root of 512 to solve for s. The result is 8, which gives the length of one edge of the cube.
SAT Math Practice Online Test Question No 10:
A solid, cone-shaped lead crystal paperweight has a height of 5 centimeters and abase diameter that is 20% larger than the height. If the density of lead crystal is3.1 g/cm3, what is the approximate mass of the paperweight? Round your answer to the nearest gram.
Show/Hide Answer Key
Correct Answer: 146
To calculate the volume of the paperweight, start by finding the radius. The question states that the diameter of the paperweight’s base is 20% larger than (120% of) its height, which is 1.2 × 5 = 6 centimeters, so the radius is half that or 3 centimeters. The volume of a cone (remember to check the formula page) is given by Vcone = (1/3)πr2h, or here (1/3)π x 32 x 5 = 15π cubic centimeters. Now, multiply this volume by the given density (3.1 g/cm3) to find that the mass of the paperweight is 15πcm3 x 3.1g/1cm3 = 46.5πg. Rounded to the nearest gram, the correct answer is 46.5 × 3.14 ≈ 146.