Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Crash Course 25 Grid Ins Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Math Crash Course 25 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
If 5/6 < (1/2)x – (1/2)y < 3/2, then what is one possible value of x – y?
Show/Hide Answer Key
Correct Answer: 5/3
Compare the variable terms between the two inequality symbols to the expression you’re looking for (1/2)x – (1/2)y is exactly half of x – y, so multiply the entire inequality by 2. The inequality becomes 5/3 < x – y < 3. Grid in any value between 1 2/3 and 3 (but not 1 2/3 or 3), such as 2 or 2.5.
SAT Math Practice Online Test Question No 2:
A subway car passes 3 stations every 10 minutes. At this rate, how many stations will it pass in 1 hour?
Show/Hide Answer Key
Correct Answer: 18
Because there are 60 minutes in an hour, the subway will pass 60 ÷ 10 = 6 times as many stations in one hour as it passes in 10 minutes. In 10 minutes, it passes 3 stations, so in 60 minutes it must pass 6 × 3 = 18 stations.
SAT Math Practice Online Test Question No 3:
Sea ice extent is a measurement of the area of the ocean with at least 15% sea ice. The graph below shows data for the extent of Arctic sea ice between 2000 and 2012 as reported by the National Snow and Ice Data Center. The line of best fit is also shown. The equation of the line is A(t) = -0.187t + 380.5, where A(t) represents the area of measurable sea ice in the Arctic Ocean in the year t.
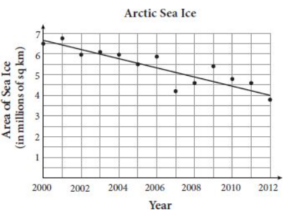
Assuming the trend of the data continues, what is the predicted area, in millions of square kilometers, of measurable Arctic sea ice in the year 2020?
Show/Hide Answer Key
Correct Answer: 2.76
A(t) = -0.187t + 380.5
A(2020) = -0.187(2020) + 380.5
A(2020) = 2.76
The predicted area of Arctic sea ice in 2020 is 2.76 million square kilometers.
SAT Math Practice Online Test Question No 4:
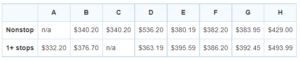
The table above is a summary of prices for round-trip airplane tickets offered by eight airlines between New York City and San Francisco. What fraction of the nonstop flights are under $400?
Show/Hide Answer Key
Correct Answer: 5/7
Getting to the Answer: There is 7 nonstop flights total (Airline A does not offer any). Of these flights, 5 cost less than $400. Therefore, the correct answer is 5/7.
SAT Math Practice Online Test Question No 5:
T = (R2/r2)√2h/√g
Suppose an open cylindrical tank has a round drain with radius r in the bottom of the tank. When the tank is filled with water to a depth of h centimeters, the time it takes for all the water to drain from the tank is given by the formula above, where R is the radius of the tank (in centimeters) and g = 980 cm/s2 is the acceleration due to gravity. Suppose such a tank has a radius of 2 meters and is filled to a depth of 4 meters. About how many minutes does it take to empty the tank if the drain has a radius of 5 centimeters? (1 meter = 100 centimeters)
Show/Hide Answer Key
Correct Answer: 24
The variables in the formula are defined in terms of centimeters, so convert each of the tank’s dimensions to centimeters: There are 100 centimeters in 1 meter, so 2 m = 200 cm and 4 m = 400 cm. Substitute these values, the radius of the drain (5 cm), and the value given for g into the formula and simplify:
T = (R2/r2)√2h/√g
= (2002/52)√2(400)/√980
= (40,000/25)√800/√980
= 1,600 x 0.903508
= 1,445.61
You should notice at this point that the result is not even close to the answer choices. The acceleration due to gravity was given in terms of seconds (seconds squared but then square rooted), so divide your final answer by 60 to find the number of minutes it takes to drain the tank: 1,445.61 ÷ 60 ≈ 24.09, or about 24 minutes.
SAT Math Practice Online Test Question No 6:
If f (x) = |x2 + 2x + 1|, what is the value of f(–4)?
Show/Hide Answer Key
Correct Answer: 9
Substitute -4 for each x in the equation and simplify:
f(x) = |x2 + 2x + 1|
f(-4) = |(-4)2 + 2(-4) + 1|
f(-4) = |16 – 8 + 1|
f(-4) = 9
Grid in 9.
SAT Math Practice Online Test Question No 7:
If x2 + 10x = 24 and x > 0, what is the value of x + 5?
Show/Hide Answer Key
Correct Answer: 7
Regardless of which method you choose, the equation must be set equal to 0 before you begin, so start by subtracting 24 from both sides: x2 + 10x – 24 = 0. To factor the equation, look for the factors of -24 that add up to 10; the numbers are -12 and 2, so the equation in factored form is (x + 12)(x – 2) = 0. Therefore, the solutions are -12 and 2. The question states that x > 0, so x must equal 2, making x + 5 = 2 + 5 = 7.
SAT Math Practice Online Test Question No 8:
(2 – i)/(5 – 2i)
If the expression above is rewritten in the form a + bi, where a and b are real numbers, what is the value of –b written as a fraction? (Note: i2 = -1)
Show/Hide Answer Key
Correct Answer: 1/29
The conjugate of 5 – 2i is 5 + 2i, multiply the numerator and denominator of the given expression by this to remove i from the denominator. Use FOIL to expand the binomial pairs, and then combine like terms to simplify. Separate the real and imaginary parts and reduce as needed. The steps for this sequence are shown here:
(2 – i)/(5 – 2i) x (5 + 2i)/(5 + 2i)
= (2 x 5) + (2 x 2i) + (-i x 5) + (-i x 2i) /25 – 4i2
= 10 + 4i – 5i – 2i2/25 – 4(-1)
= 10 – i – 2(-1)/29
= 12 – i/29
= 12/29 – (1/29)i
The question asks for the value of –b (and b is the coefficient of the imaginary part), so the correct answer is -(-1/29) = 1/29
SAT Math Practice Online Test Question No 9:
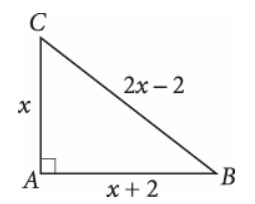
In the figure above, ΔABC is a right triangle. What is the value of x?
Show/Hide Answer Key
Correct Answer: 6
Getting to the Answer: Using the Pythagorean theorem, we know that AB2 + AC2 = BC2. Substitute the side lengths and simplify using FOIL: x2 + (x + 2)2 = (2x – 2)2
x2 + (x + 2)(x + 2) = (2x – 2)(2x – 2)
x2 + x2 + 2x + 2x + 4 = 4x2 – 4x – 4x + 4
2x2 + 4x + 4 = 4x2 – 8x + 4
Now, solve the quadratic equation by moving everything to one side of the equal sign (so the equation equals 0) and factoring it:
0 = 2x2 – 12x
0 = 2x(x – 6)
Finally, set each factor equal to 0 to find that x = 0 and x = 6. Because a side length cannot be 0, x (and therefore AC) must be 6.
SAT Math Practice Online Test Question No 10:
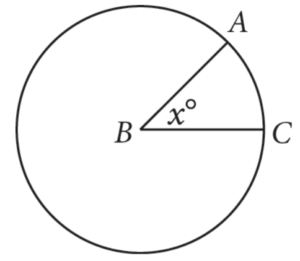
In the figure above, the ratio of the circumference of circle B to the length of minor arc AC is 8:1. What is the value of x?
Show/Hide Answer Key
Correct Answer: 45
Use the ratio of the circumference to the arc length and your knowledge of degree measures in a circle to write a proportion, and then solve for the missing length:
1/8 = x/360
360 = 8x
45 = x
Grid in 45.