Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Questions Test 6 Grid Ins Problems with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Math Questions Test 6 Grid Ins Problems with Answer Keys
SAT Math Practice Online Test Question No 1:
Set R consists of all the one-digit prime numbers. Set S contains all of the elements of Set R, as well as an additional positive integer, x.
If the sum of all of the elements of Set S is 30, what is the value of x2 – 11x – 25?
Show/Hide Answer Key
Correct Answer: 1
First, you need to determine the content of Set R. If Set R consists of all the one-digit prime numbers, then R = {2, 3, 5, 7}.
The sum of the elements of Set S would therefore be 2 + 3 + 5 + 7 + x = 30. Combine like terms: 17 + x = 30.
Subtract 17 from both sides, and you find x = 13. Plug x = 13 into the equation and solve: (13)2 – 11(13) – 25 = 1.
SAT Math Practice Online Test Question No 2:
A rectangular box has a volume of 24. If the length is halved and the height is tripled, what will be the new volume of the box?
Show/Hide Answer Key
Correct Answer: 36
Pick any values for the length, width, and height that will give you a volume of 24.
If you say the length is 2, the height is 3, and the width is 4, then the new length, height, and width will be 1, 9, and 4 respectively. The new volume is 36. No matter what numbers you set for the initial length, width, and height, you will always get 36 for the new volume.
SAT Math Practice Online Test Question No 3:
Dan orders a soccer jersey online. If the jersey costs 40 euros and one euro is worth 1.2 dollars, how many dollars did Dan pay for the jersey?
Show/Hide Answer Key
Correct Answer:
48 Set up a proportion: 1 euro/1.2 dollars = 40 euros/x dollars.
Cross-multiply and get x = 1.2 × 40 = 48.
SAT Math Practice Online Test Question No 4:
h(t) = (1/2)at2
As a space probe descends to the surface of Mars, its distance in meters above the surface can be modeled by the equation above. If t is the time in seconds it will take the probe to reach the surface, and it takes the probe 8 seconds to descend the final 120 meters to the surface, what is the value of the deceleration constant a?
Show/Hide Answer Key
Correct Answer: 15/4 or 3.75
According to the question, h(t) = 120 and t = 8.
Plug these values into the function to get 120 = (1/2)a(82). Simplify the equation to get 120 = 1/2a(64) and 120 = 32a.
Solve for a to get a = 3.75. The correct answer is 3.75.
SAT Math Practice Online Test Question No 5:
1.3g + 1.7h = 5
3h = 20 + 13g
Based on the system of equations above, what is the value of h?
Show/Hide Answer Key
Correct Answer: 7/2 or 3.5
First, get rid of the decimals in the first equation by multiplying the first equation by 10 to get 13g + 17h = 50.
In the second equation, move all the variables to the left of the equal sign to get -13g + 3h = 20. Whenever there are two equations with the same two variables, they can be solved simultaneously by adding or subtracting them.
The key is to get one variable to disappear. Stack the equations on top of each other and add them.
[(13g + 17h = 50) – (13g + 3h = 20)] = (20h = 70). Therefore, h = 70/20.
Because this number is too large to grid in, either reduce the fraction to 7/2 or convert the fraction to the decimal 3.5.
SAT Math Practice Online Test Question No 6:
When (x2 + 2x – 3)(2x + 5) – (x + 1)(x – 1)(x + 3) is expressed in the form ax3 + bx2 + cx + d, what is the value of a + b + c + d ?
Show/Hide Answer Key
Correct Answer: 0
Start by multiplying the terms together. To multiply (x2 + 2x – 3)(2x + 5), multiply each term in the left parenthesis by each term in the right parenthesis to get 2x3 + 5x2 + 4x2 + 10x – 6x – 15.
Combine like terms to get 2x3 + 9x2 + 4x – 15. To multiply (x + 1)(x – 1)(x + 3), do one set of parentheses first; then multiply that product by the remaining parenthesis. You may notice that (x + 1)(x – 1) is a common quadratic, which equals x2 – 1.
Then you need to multiply x2 – 1 by (x + 3). As you did before, multiply each term in the first parenthesis by each term in the second to get x3 + 3x2 – x – 3. Now you can do (2x3 + 9x2 + 4x – 15) – (x3 + 3x2 – x – 3).
It is easiest to distribute the negative sign into the second parenthesis: (2x3 + 9x2 + 4x – 15) + (-x3 – 3x2 + x + 3). Now you can combine like terms to get x3 + 6x2 + 5x – 12. This is in the form ax3 + bx2 + cx + d, so a = 1, b = 6, c = 5, and d = -12. This means a + b + c + d = 1 + 6 + 5 + (-12) = 0.
SAT Math Practice Online Test Question No 7:
Once an insect reaches its larval stage, its mass increases linearly for a short period and then slows down as it prepares to enter pupation. Suppose the larva of a certain species has an initial mass of 10 grams and grows linearly from t = 0 to t = 48 hours of its larval stage. If after 48 hours, the mass of the larva is 14 grams, what was its mass in grams at t = 6 hours?
Show/Hide Answer Key
Correct Answer: 10.5 or 21/2
Difficulty: Medium
Category: Heart of Algebra / Linear Equations
Strategic Advice: The keyword in this question is linear. In a real-world scenario that involves a constant rate of change, you almost always need to find the slope and the initial amount so you can write an equation. The question states that the initial mass of the larva was 10 grams, so all you need to do is find the slope.
Getting to the Answer: Write the information given in the question as ordered pairs (time, mass) so you can find the slope. At t = 0, the larva has a mass of 10 grams, so one pair is (0, 10). After 48 hours, the larva has a mass of 14 grams, so a second pair is (48, 14). Now, use the slope formula: m = (y2 – y1)/(x2 – x1) = (14 – 10)/(48 – 0) = 4/48 = 1/12.
The equation is y = (1/12)x + 10, where y represents the mass of the larva after x hours. Substitute 6 for x to find the mass after 6 hours: (1/12)6 + 10 = 6/12 + 10 = 10.5 grams.
SAT Math Practice Online Test Question No 8:
If 0.2x + 1.8 = 3 – 0.6x, what is the value of x?
Show/Hide Answer Key
Correct Answer: 3/2 or 1.5
Difficulty: Easy
Category: Heart of Algebra / Linear Equations
Strategic Advice: Don’t waste time trying to combine decimal numbers. Instead, multiply all of the numbers in the equation by 10 to get rid of the decimals. The resulting equation is much easier to solve.
Getting to the Answer: Multiplying each term in the equation by 10 moves the decimal one place to the right, which eliminates all the decimals.
10(0.2x + 1.8 = 3 – 0.6x)
2x + 18 = 30 – 6x
8x = 12
x = 12/8 = 3/2
SAT Math Practice Online Test Question No 9:
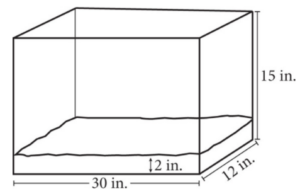
The figure above shows a fish tank with sand in the bottom. If the water level is to be 3 inches below the top, how many cubic inches of water is needed to fill the tank?
Show/Hide Answer Key
Correct Answer: 3600
Difficulty: Medium
Category: Additional Topics in Math / Geometry
Strategic Advice: Determine the dimensions of the tank in which there will be water. Then, use the formula for finding the volume of a rectangular prism: Volume = length × width × height.
Getting to the Answer: The tank is 30 inches long, 15 inches tall, and 12 inches wide. The sand and the space left at the top of the tank do not affect the length or the width, only the height of the water. There are 2 inches of sand in the bottom and 3 inches of space left at the top, which means the height of the water is 15 – 2 – 3 = 10 inches. Use the formula Volume = l × w × h = 30 × 12 × 10. To multiply the numbers without a calculator, multiply 3 × 1 × 12 = 36 and then add two zeros to get 3,600 cubic inches of water.
SAT Math Practice Online Test Question No 10:
g(x) = { x2 – 1, if x ≤ 0 }
g(x) = { (x2/3) + 1, if 0 < x ≤ 3}
g(x) = {5x + 3, if x > 3}
For the piecewise-defined function g(x) shown above, what is the value of g(2)?
Show/Hide Answer Key
Correct Answer: 7/3 or 2.33
Difficulty: Medium
Category: Passport to Advanced Math / Functions
Strategic Advice: Piecewise defined functions look intimidating, but they are usually very simple functions they’d just written in pieces. Your job is to figure out which piece of the function you need to use to answer the question.
Getting to the Answer: The right-hand side of each piece of the function tells you what part of the domain (which x-values) goes with that particular function. In this function, only values of x that are less than zero go with the top function, values of x between 0 and 3 go with the middle function, and values of x that are greater than 3 go with the bottom function. Because 2 is between 0 and 3, plug it into the middle function and simplify g(2) = (2)2/3 + 1 = 4/3 + 1 = 4/3 + 3/3 = 7/3.



