Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Practice Online Test 7 Grid Ins Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Math Practice Online Test 7 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
If 6e(e + 3) = 3e(2e + 4) + 5, what is the value of e ?
Show/Hide Answer Key
Correct Answer: 5/6 or 0.833
Distribute the 6e on the left side of the equation and the 3e on the right side of the equation to get 6e2 + 18e = 6e2 + 12e + 5.
Subtract 6e2 from both sides of the equation to get 18e = 12e + 5. Solve for e to get 6e = 5, so e = 5/6. The correct answer is 5/6.
SAT Math Practice Online Test Question No 2:
An ice cream cart vendor sells 50 popsicles on an average fall day. During the summer, the ice cream cart vendor sells 7 less than twice as many popsicles per day as he does on the average fall day. How many popsicles does the ice cream cart vendor sell in 6 summer days?
Show/Hide Answer Key
Correct Answer: 558
During the summer the ice cream vendor sells an average of 2(50) – 7 = 93 popsicles per day. Over 6 summer days, 93 × 6 = 558 popsicles are sold. The correct answer is 558.
SAT Math Practice Online Test Question No 3:
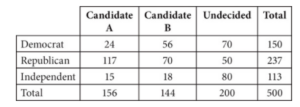
The table above illustrates the results of a political poll. Five hundred voters were first asked whether they were registered as Democrat, Republican, or Independent. The voters were then asked whether they planned to vote for Candidate A, for Candidate B, or were Undecided. What percent of the registered Democrats plan to vote for Candidate A ? (Disregard the percent symbol when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 16
To find the percent of registered Democrats planning to vote for Candidate A, divide the number of Democrats planning to vote for Candidate A by the total number of registered Democrats: 24/150 = 0.16 = 16%, which makes 16 the correct answer.
SAT Math Practice Online Test Question No 4:
The Nile is a track & field athlete at North Sherahan High School. He hopes to qualify for the Olympic Games in his best field event, the javelin throw. He experiments with different javelin weights to build his arm strength and currently measures the results in feet.
Show/Hide Answer Key
Correct Answer: 195
Use the definition of inverse proportion: x1y1 = x2y2. Plug in 1.5 for x1, 260 for y1, 2 for x2, and solve for y2: (1.5)(260) = (2)(y2); 390 = 2y2. Divide both sides by 2, and you find y2 = 195.
SAT Math Practice Online Test Question No 5:
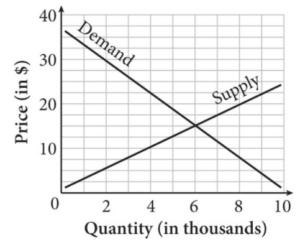
Retail businesses strive to price their products so that they sell as many as possible without losing money. Economic equilibrium is the price point at which the supply for a product is equal to the demand for that product. The graph above models this scenario. According to the graph, at what price in dollars will supply equal demand for this particular product?
Show/Hide Answer Key
Correct Answer: 15
Difficulty: Easy
Category: Heart of Algebra / Systems of Linear Equations
Strategic Advice: Sometimes, being able to interpret a graph that models a real-world scenario is enough to answer a question. Just be sure to read the axis labels carefully.
Getting to the Answer: The equilibrium price occurs when the supply and demand are equal. Graphically, this means where the two lines intersect. The lines intersect at the point (6, 15). You can see from the axis labels that price is plotted along the y-axis, so the equilibrium price is $15.
SAT Math Practice Online Test Question No 6:
Several values for the functions f(x) and g(x) are shown in the tables. What is the value of f(g(-1))?
Show/Hide Answer Key
Correct Answer: 4
Difficulty: Medium
Category: Passport to Advanced Math / Functions
Strategic Advice: The notation (f(g(x)) indicates a composition of two functions which is read “f of g of x.” It means that the output when x is substituted in g(x) becomes the input for f(x).
Getting to the Answer: First, use the table on the right to find that g(-1) is 2. This is your new input. Now, use the table on the left to find f(2), which is 4.
SAT Math Practice Online Test Question No 7:
The tables above represent data points for two linear equations. If the two equations form a system, what is the x-coordinate of the solution to that system?
Show/Hide Answer Key
Correct Answer: 0
Difficulty: Medium
Category: Heart of Algebra / Systems of Linear Equations
Strategic Advice: The solution to the system is the point that both tables will have in common, but the tables, as given, do not share any points. You could use the data to write the equation of each line and then solve the system, but this would use up valuable time on Test Day. Instead, whenever data is presented in a table, look for patterns that can be extended.
Getting to the Answer: In the table on the left, the x-values decrease by 1 each time and the y-values increase by 3. In the table on the right, the x-values increase by 2 each time and the y-values increase by 1. Use these patterns to continue the tables.
The point (0, 7) satisfies both equations, so the x-coordinate of the solution to the system is 0.
SAT Math Practice Online Test Question No 8:
If g(x) = 2x3 – 5x2 + 4x + 6, and P is the point on the graph of g(x) that has an x-coordinate of 1, then what is the y-coordinate of the corresponding point on the graph of g(x – 3) + 4?
Show/Hide Answer Key
Correct Answer: 11
Strategic Advice: This question is, for the most part, conceptual. Start by finding the y-coordinate of P in the original equation. Then, perform the transformation on the coordinates (rather than the function) to save yourself valuable time.
Getting to the Answer: Substitute 1 for x in the original equation. Graphically, the resulting value of g(1) is the y-coordinate of the point.
g(x) = 2x3 – 5x2 + 4x + 6 = 2(1)3 – 5(1)2 + 4(1) + 6 = 2 – 5 + 4 + 6 = 7
The point on the graph of g(x) is (1, 7). Now, the question asks for the y-coordinate of the corresponding point on the transformed graph. When performing transformations, the operations grouped with the x are performed on the x-coordinate, and the operations not grouped with the x are performed on the y-coordinate. So, add 4 to 7 to find that the y-coordinate of the point on the transformed graph is 11.
SAT Math Practice Online Test Question No 9:
If 1/3 ≤ 2 – d/6 ≤ 5/4, what is the minimum possible value of d?
Show/Hide Answer Key
Correct Answer: 9/2 or 4.5
Strategic Advice: Choose the best strategy to answer the question. Here, the fractions make it look more complicated than it really is, so start by clearing the fractions by multiplying everything by 12.
Getting to the Answer: You don’t need to separate this compound inequality into pieces. Just remember, whatever you do to one piece, you must do to all three pieces, and don’t forget to reverse the inequality symbols if you multiply or divide by a negative number.
1/3 ≤ 2 – d/6 ≤ 5/4
12(1/3) ≤ 12 (2 – d/6) ≤ 12(5/4)
4 ≤ 24 – 2d ≤ 15
-20 ≤ -2d ≤ -9
10 ≥ d ≥ 9/2
The question asks for the minimum possible value of d, so turn the inequality around so that smaller numbers are written first: 9/2 ≤ d ≤ 10, making the minimum value 9/2, or 4.5.
SAT Math Practice Online Test Question No 10:
What is one possible solution to the rational equation x/(x – 1) – 2/x = 1/(x – 1)?
Show/Hide Answer Key
Correct Answer: 2
Strategic Advice: Solving a rational equation takes patience and a good deal of algebraic manipulation. You’ll need to find a common denominator and multiply both sides of the equation by that denominator. The next steps will depend on what kind of equation results from the first steps.
Getting to the Answer: Start by multiplying both sides of the equation (all three terms) by the common denominator, which is x(x + 1). Try to write neatly, especially when canceling terms, so you don’t lose track of anything.
x(x) – 2(x – 1) = x(1)
x2 – 2x + 2 = x
The resulting equation is quadratic, so set it equal to zero and either try to factor it or use the quadratic formula to solve it.
x2 – 2x + 2 = x
x2 – 3x + 2 = 0
(x – 1)(x – 2) = 0
x – 1 = 0 or x – 2 = 0
x = 1 or x = 2
Be careful here-whenever there is a variable in the denominator of an equation, you must check to make sure that the solutions do not result in division by zero. The solution x = 1 does result in division by 0, so it is invalid. That means the only correct solution is x = 2.