Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Mathematics Practice Test 21 Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Mathematics Practice Test 21 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
If one pound of grain can feed either 5 chickens or 2 pigs, then ten pounds of grain can feed 20 chickens, and how many pigs?
Show/Hide Answer Key
Correct Answer: 12
Problem Solving/Data Analysis (word problem) MEDIUM-HARD
This one is a bit trickier than it looks. We have 10 pounds of grain and have used it to feed 20 chickens. Since one pound of grain feeds 5 chickens, proportionally we need 4 pounds of grain to feed 20 chickens. This leaves us 10 – 4 = 6 pounds of grain to feed the pigs. Since 1 pound of grain can feed 2 pigs, proportionally 6 pounds of grain can feed 12 pigs.
SAT Math Practice Online Test Question No 2:
What number is 40% greater than the sum of 40 and 80?
Show/Hide Answer Key
Correct Answer: 168
Algebra (percents) EASY
The sum of 40 and 80 is 120, and 40% of 120 is (0.40) (120) = 48, so the number that is 40% greater than 120 is 120 + 48 = 168. Also, remember that increasing a number by 40% is equivalent to multiplying it by 1.4.
SAT Math Practice Online Test Question No 3:
The sum of two numbers is four times their difference. The smaller of these numbers is 15. What is the greater number?
Show/Hide Answer Key
Correct Answer: 25
Algebra (word problems) EASY
Let’s let x be the larger number. 15 is the smaller number.
The sum of the numbers is four times their difference: x + 15 = 4(x – 15)
Distribute: x + 15 = 4x – 60
Add 60: x + 75 = 4x
Subtract x: 75 = 3x
Divide by 3: 25 = x
SAT Math Practice Online Test Question No 4:
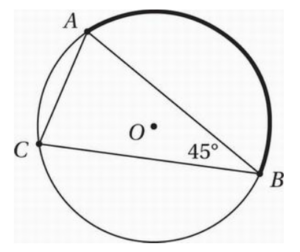
In the figure above, the circle with center O has a circumference of 50, and AB = BC. What is the length of arc AB?
Show/Hide Answer Key
Correct Answer: 75/4 or 18.75
Special Topics (arcs and triangles) MEDIUM-HARD
Let’s start by drawing the three radii OA, OB, and OC. Since these radii are all congruent, and because AB = BC, the triangles AOB and COB are congruent (by the SSS Theorem). This implies that OB bisects angle ABC, so the base angles of both isosceles triangles must have measured 45°/2 = 22.5°. Therefore, angle AOB, which is the central angle for arc AB, must-have measure 180° – 22.5° – 22.5° = 135°. Now we can use the fact that the circumference of the circle is 50 to find the length of arc AB.
mAB/135° = 50/360° Let x = mAB and cross multiply: 360x = 6,750
Divide by 360: x = 75/4 = 18.75
SAT Math Practice Online Test Question No 5:
If a shipment of the fruit contains 6 tons of bananas, 4 tons of grapes, 2 tons of apples, and 3 tons of oranges, what fraction of the shipment, by weight, is oranges?
Show/Hide Answer Key
Correct Answer: .2 or 1/5
Problem Solving and Data Analysis (ratios) EASY
The total weight of the shipment is 6 + 4 + 2 + 3 = 15, and the total weight of oranges is 3, so the fraction of the shipment that is oranges is 3/15 5 .2
SAT Math Practice Online Test Question No 6:
Connor and Joachim collaborated to write a computer program that consisted of 3,500 lines of code. If Joachim wrote 600 more lines of code than Connor did, how many lines of code did Connor write?
Show/Hide Answer Key
Correct Answer: 1450
If Connor wrote x lines of code, then Joachim wrote x + 600 lines of code. Together they wrote (x) + (x + 600) = 3,500 lines of code:
x + x + 600 = 3,500
Simplify and subtract 600: 2x = 2,900
Divide by 2: x = 1,450
Therefore Connor wrote 1,450 lines of code.
SAT Math Practice Online Test Question No 7:
If I = FV/(1 + r)n
The formula above indicates the initial investment, I, that must be made in an account with an annual interest rate of r to ensure a future value of FV after n years.
To the nearest dollar, what initial investment should be made in an account that earns 20% annually (r = 0.20) to ensure a future value of $432 in two years? (Ignore the $ sign when gridding your answer. That is, enter $125 as 125.)
Show/Hide Answer Key
Correct Answer: 300
Problem Solving and Data Analysis (formula analysis) MEDIUM
This requires simply substituting into the formula: I = 432/(1 + 0.2)2 = 432/1.44 = 300
SAT Math Practice Online Test Question No 8:
17(6x – 50) = 204(7/24[x])
For what value of x is the equation above true?
Show/Hide Answer Key
Correct Answer: 20
17(6x – 50) = 204(7/24[x])
6x – 50 = 12(7/24[x])
6x – 50 = 7/2(x)
(12/2)x – (7/2)x = 50
(5/2)x = 50
5x = 100
x = 20
SAT Math Practice Online Test Question No 9:
[3(h + 2) – 4]/6 = h(7 x 2 – 5)/2
In the equation above, what is the value of h?
Show/Hide Answer Key
Correct Answer: 1/12
[3(h + 4) – 4]/6 = h(7 x 2 – 5)
(3h + 6 – 4)/6 = [h(14 – 5)]/2
(3h + 2)/6 = 9h/2
2(3h + 2) = 6(9h)
6h + 4 = 54h
4 = 48h
h = 4/48 = 1/12
SAT Math Practice Online Test Question No 10:
An office has 27 employees. If there are seven more women than men in the office, how many employees are men?
Show/Hide Answer Key
Correct Answer: 10
Getting to the Answer: There are 27 total employees at the office, all either men or women, so m (the number of men) + w (the number of women) = 27. There are seven more women than men, so w = m + 7. Substitute m + 7 for w into the first equation:
m + w = 27
m + (m + 7) = 27
2m + 7 = 27
2m = 20
m = 10
The question asks for the number of men (m), so you’re done! There are 10 men in the office.