Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Course 23 Grid Ins Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Math Course 23 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
hx + 4y = -3
The equation above is the equation of a line in the xy-plane, and h is a constant. If the slope of this line is -13, what is the value of h?
Show/Hide Answer Key
Correct Answer: 52
Algebra (linear equations) MEDIUM
The slope of a linear equation in “standard form,” ax + by = c is equal to -a/b. Therefore, the linear equation hx + 4y = -3 has a slope of –h/4. If this slope equals -3, then -h/4 = -13.
Multiply by -4: h = 52
SAT Math Practice Online Test Question No 2:
An Internet service provider offers three different plans for residential users. Plan A charges users $500 for the first year of service and $80 per month thereafter. Plan B charges users $68 per month. Plan C is a “high speed” plan that offers 200% higher speeds for $92 per month.
Isabelle is now considering switching to either Plan B or Plan C for her home business, but she calculates that having the “high speed” plan will save her only approximately 45 minutes of work each month. At what minimum hourly rate, in dollars per hour, would she have to value her work (that is, how much more would she have to value one hour of free time over one hour of work time) for Plan C to be worth the extra cost over Plan B?
Show/Hide Answer Key
Correct Answer: 32
Problem Solving (extended thinking) HARD
Since Plan C costs $92 per month and Plan B costs $68 per month, Plan C costs $92 – $68 = $24 more dollars per month than plan B. Since shifting plans would save her only 45 minutes of work, or 3/4 hour, each month, she would have to value one hour of free time over one hour of work time at $24/(¾ hour) = $32.
SAT Math Practice Online Test Question No 3:
dn = 13n + 200
The formula above represents the number of donuts, dn, that a bakery sold on the nth day of a festival. If the festival lasted 3 days, what was the total number of donuts that the bakery sold during the festival?
Show/Hide Answer Key
Correct Answer: 678
Problem Solving and Data Analysis (data from the formula) MEDIUM
The formula indicates how many donuts were sold on each day of the festival. One day 1, the bakery sold 13(1) + 200 = 213 donuts. On day 2, the bakery sold 13(2) + 200 = 226 donuts. On day 3, the bakery sold 13(3) + 200 = 239 donuts, for a total of 213 + 226 + 239 = 678 donuts
SAT Math Practice Online Test Question No 4:
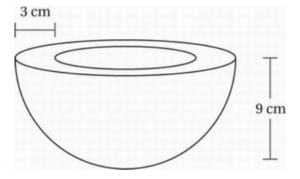
The figure above shows a hemispherical bowl made of glass. The bowl is 9 centimeters high and the glass is 3 centimeters thick. A second bowl is to be constructed to scale with the original bowl but with one-half the height and diameter. The smaller bowl can hold a maximum of kπ cubic centimeters of water. What is the value of k? (The volume of a sphere with radius r is given by the formula V = (4/3)πr3.
Show/Hide Answer Key
Correct Answer: 18
Additional Topics (volumes and similarity) HARD
The radius of the inside of the larger bowl is 9 – 3 = 6 centimeters, so the radius of the smaller bowl is 3 centimeters. The volume of the smaller bowl is therefore 1/2([4/3]π(3)3) = 4π(27)/6 = 18π
Therefore, k = 18.
SAT Math Practice Online Test Question No 5:
1/2(6x – 4) – (3 – x) = ax + x + b
If the equation above has infinitely many solutions, what is the value of a – b?
Show/Hide Answer Key
Correct Answer: 8
Difficulty: Hard
Category: Heart of Algebra / Linear Equations
Strategic Advice: A linear equation has infinitely many solutions when once simplified, the left side of the equation is equal to the right side (known as an identity). For example, if the simplified form of an equation is 5 = 5, or even 2x + 5 = 2x + 5, then the equation has infinitely many solutions.
Getting to the Answer: Simplify both sides of the equation as much as possible. Then examine the terms that remain:
1/2([6x – 4] – [3 – x]) = ax + x + b
3x – 2 – 3 – (-x) = ax + x + b
3x – 2 – 3 + x = ax + x + b
4x – 5 = x(a + 1) + b
For the left side of the equation to equal the right side, the coefficient of x must be the same on each side, and the constant must be the same on each side: a + 1 = 4, so a = 3, b = -5
The question asks for a – b, so the correct answer is 3 – (-5) = 3 + 5 = 8.
SAT Math Practice Online Test Question No 6:
x + y = -6
y – 4x = 4
If the ordered pair (x, y) satisfies the system of equations shown above, what is the value of xy?
Show/Hide Answer Key
Correct Answer: 8
Difficulty: Medium
Category: Heart of Algebra / Systems of Linear Equations
Strategic Advice: When answering a Grid-in question, it is particularly important to check that you answered the right question before you grid in your answer.
Getting to the Answer: Use substitution or combination (elimination) to find the solution to the system. If you choose a combination, the second equation needs to be rearranged so that like terms are lined up vertically, and you’ll need to multiply the first equation by 4 so that the x terms are eliminated when you add the equations:
4[x + y = -6] → 4x + 4y = -24
y – 4x = 4 → -4x + y = 4
5y = -20 Thus, y = -4
From the first equation, x + y = -6 gives x + (-4) = -6, so x = -2. The question asks for the value of xy, so multiply to get (-2) × (-4) = 8.
SAT Math Practice Online Test Question No 7:
Two moonflower vines are growing on a trellis in Mallory’s backyard. She bought the first vine when it was 11 inches long and found that it grows at a rate of 0.25 inches per day. Exactly 20 days later, Mallory bought the second vine, which started at 24inches long and has a growth rate of 0.125 inches per day. How many days will Malloryhave had the first vine when the lengths of the two vines are the same?
Show/Hide Answer Key
Correct Answer: 84
Difficulty: Hard
Category: Heart of Algebra / Systems of Linear Equations
Strategic Advice: Use what you know about real-world scenarios and linear equations to write a system of equations. In a real-world scenario, a rate is the same as the slope and a starting amount is a y-intercept.
Getting to the Answer: Let d represent the number of days of vine growth for the second vine, and let l represent the length of each vine. Mallory’s first vine grows at a rate of 0.25 inches per day and was 11 inches long when she bought it (20 days before d), so the length of the first vine can be represented by the equation l = 0.25(d + 20) + 11, which simplifies to l = 0.25d + 16. The second vine started at 24 inches and grows 0.125 inches per day, so the equation that represents its length is l = 0.125d + 24. To determine when the lengths of the vines will be the same, set the two equations equal to each other and solve for d:
0.25d + 16 = 0.125d + 24
0.125d = 8
d = 64
Don’t stop yet-the question asked how many days Mallory had the first vine when the lengths of the two vines are the same, so add 20 to d to account for the time that she had the first vine before buying the second vine. This means the correct answer is 84.
SAT Math Practice Online Test Question No 8:
The variables x and y represent numbers for which the statements x – y > 300 and y/x = 0.625 are true. What is the smallest integer that x can equal?
Show/Hide Answer Key
Correct Answer: 801
Difficulty: Hard
Category: Heart of Algebra / Inequalities
Strategic Advice: When you have two unknowns, try to write one in terms of the other to simplify the situation.
Getting to the Answer: Solve the equation for y in terms of x:
y/x = 0.625
y = 0.625x
Substitute this value for y into the inequality and simplify: x – y > 300
x – 0.625x > 300
0.375x > 300
x > 300/0.375
x > 800
Be careful-the inequality specifies that x must be greater than 800, so the least possible integer value of x is 801.
SAT Math Practice Online Test Question No 9:
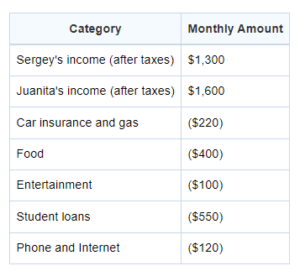
In preparation for buying a house, Sergey and Juanita draft a budget to see how much they can afford. Their monthly spending and income are shown in the table. Numbers in parentheses indicate expenses (money being spent); numbers without parentheses indicate income (money being earned). Sergey and Juanita will not buy a house unless they can save at least $400 a month after all expenses, including the new mortgage payment and property taxes, are paid.
The couple would like to buy a house that costs $230,400, for which the monthly mortgage payment would be $730, and the annual property taxes would be 2.5% of the purchase price. By what percent could Sergey and Juanita cut their monthly food spending to buy this particular house and meet their criteria for purchasing a house? (Ignore the percent sign and grid in your answer as a whole number.)
Show/Hide Answer Key
Correct Answer: 25
Difficulty: Medium
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: When answering a Grid-in question, be sure to follow any directions that are given about how to enter your answer.
Getting to the Answer: First, compute the monthly property taxes of the home: $230,400 x 2.5% ÷ 12 = $480 per month. Next, tabulate Sergey and Juanita’s monthly gains and losses if they buy the house: $1,300 + $1,600 – $220 – $400 – $100 – $550 – $120 – $730 – $480 = $300. This means they can save $300 each month. However, they won’t buy the house unless they can save $400 per month. To make up the deficit, they could shave $100 off their monthly $400 food bill, which is $100/$400 = 0.25. Be sure to follow directions (enter the answer as a whole number): 0.25 = 25%, so grid in 25.
SAT Math Practice Online Test Question No 10:
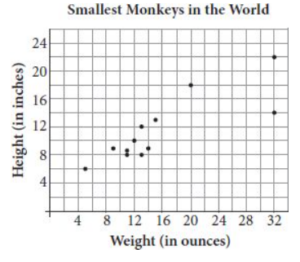
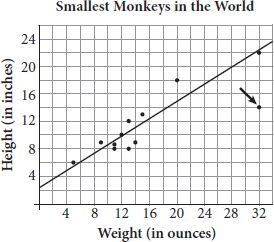
There are more than 250 known species of monkeys in the world. The scatterplot above shows the average height and weight of 12 species of particularly small monkeys, most of which live in the Amazon Basin of South America. What is the height, in inches, of the monkey represented by the data point that is farthest from the line of best fit (not shown)?
Show/Hide Answer Key
Correct Answer: 14
Difficulty: Medium
Category: Problem Solving and Data Analysis / Scatterplots
Strategic Advice: When working with scatterplots, a line of best fit should be drawn so that about half the data points are above the line and half are below the line.
Getting to the Answer: Draw in the line of best fit. It doesn’t have to be perfect you just need to get an idea of where it should be.
The data point that is farthest from the line is located at (32, 14). Height is plotted on the y-axis, so this data point represents a monkey that is 14 inches tall.