Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Maths Practice Test 44 Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Maths Practice Test 44 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
If 5x – 4 = x – 1, what is the value of x?
Show/Hide Answer Key
Correct Answer: 0.75
All you have to do is solve for x:
5x – 4 = x – 1
5x = x + 3
4x = 3
x = 3/4 or 0.75
SAT Math Practice Online Test Question No 2:
Let f (x) = x2 – 5. If f (6) – f (4) = f (y), what is | y |?
Show/Hide Answer Key
Correct Answer: 5
f(6) = 62 – 5 = 31. f(4) = 42 – 5 = 11. So f(6) – f(4) = 20.
You then find y such that y2 – 5 = 20. y2 = 25, so y = 5 or –5, and the absolute value of y = 5.
SAT Math Practice Online Test Question No 3:
Points E, F, G, and H lie on a line in that order. If EG = 5/3 EF and HF = 5FG, then what is EF/HG?
Show/Hide Answer Key
Correct Answer: 0.375
Because the question doesn’t give you a figure, you should draw one. Then plug in some values.
If EG = 5/3 EF, then you can make EF = 3 and EG = 5.
That means FG must be 2. If HF = 5FG, then HF = 5(2) = 10. If HF = 10 and FG = 2, then HG = 8.
So EF/HG = 3/8 or 0.375.
SAT Math Practice Online Test Question No 4:
Y is a point on XZ such that XY = [1/2]XZ. If the length of YZ is 4a + 6, and the length of XZ is 68, what is the value of a?
Show/Hide Answer Key
Correct Answer: 7
It would definitely help to draw out this question:
XY = [1/2]XZ, which means Y is the midpoint of XZ. So XY = YZ, and therefore YZ = [1/2]XZ.
If YZ = 4a + 6 and XZ = 68, then 4a + 6 = [1/2]68.
Now just solve for a: 4a + 6 = [1/2]68
4a + 6 = 34
4a = 28
a = 7
SAT Math Practice Online Test Question No 5:
Twenty bottles contain a total of 8 liters of apple juice. If each bottle contains the same amount of apple juice, how many liters of juice is in each bottle?
Show/Hide Answer Key
Correct Answer: 0.4
You can solve this question by setting up a proportion.
There are 8 liters in 20 bottles of juice, and you need to find out how many liters are in one bottle. Here’s what the proportion looks like
8/20 = x/1.
Solve for x, and your answer is 2/5 or 0.4.
SAT Math Practice Online Test Question No 6:
One-fifth of the cars in a parking lot are blue and 1/2 of the blue cars are convertibles. If 1/4 of the convertibles in the parking lot are blue, then what percent of the cars in the lot are neither blue nor convertibles? (Disregard the % sign when gridding your answer.)
Show/Hide Answer Key
Correct Answer: 50
You don’t know how many cars are in the parking lot, so you can plug in a number.
Let’s say there are 40 cars in the parking lot. Now read through the question; if 1/5 of the cars are blue, there are 8 blue cars. If 1/2 of the blue cars are convertibles, there are 4 blue convertibles.
If 1/4 of all the convertibles are blue, and there are 4 blue convertibles, that means there are 16 convertibles altogether. The question asks what percent of the cars are neither blue nor convertibles.
At this point, the question becomes a group question, and you have a formula for solving such questions: total = group 1 + group 2 – both + neither. In this question, the total is 40 cars, group 1 is the 8 blue cars, and group 2 is the 16 convertibles.
You also know that 4 cars are both blue and convertibles. Now just plug those values into the formula: 40 = 16 + 8 – 4 + n.
Then solve for n, which equals 20. So 20 out of the total 40 cars are neither blue nor convertibles: 20/40 = 1/2 = 50%.
SAT Math Practice Online Test Question No 7:
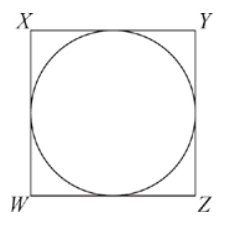
In the figure above, a circle is inscribed in square WXYZ. If the area of the circle is 400π, what is the area of WXYZ?
Show/Hide Answer Key
Correct Answer: 1600
If the area of the circle is 400π, then you can figure out its radius. A = πr2 so 400 = πr2, and the radius is 20.
The diameter of the circle is twice the radius, or 40. Because this circle is inscribed in the square, you know that the diameter of the circle is equal to one side of the square, so you know that each side is equal to 40.
The area of the square is 40 × 40 = 1,600.
SAT Math Practice Online Test Question No 8:
Jeannette’s average (arithmetic mean) score for six tests was 92. If the sum of the scores of two of her tests was 188, then what was her average score for the other four tests?
Show/Hide Answer Key
Correct Answer: 91
Let’s begin by using our Average Pie.
If Jeanette’s average on 6 tests was 92, then you know that her total score on all six tests must be 92 × 6 = 552.
Two of those test scores add up to 188; if you remove those two tests, the other four tests must have a sum that adds up to 552 – 188, or 364.
So the average of these four tests will be 364 ÷ 4, or 91.
SAT Math Practice Online Test Question No 9:
Tiles numbered 1 through 25 are placed in a bag. If one tile is removed at random, what is the probability that the number on the tile is a prime number?
Show/Hide Answer Key
Correct Answer: 0.36
Probability in this case is the number of prime numbers divided by the total number of possibilities (25 numbers).
The prime numbers between 1 and 25 are 2, 3, 5, 7, 11, 13, 17, 19, and 23. So, there are 9 prime numbers. The probability is 9/25 or 0.36.
SAT Math Practice Online Test Question No 10:
If the distance from (2, 6) to (1, b) is a, a = (|-1| + 16)1/2, and b < a, what is the value of b?
Show/Hide Answer Key
Correct Answer: 2
Absolute value is the distance from zero to the number on the number line, or in other words, the positive version of the number. So, (|-1| + 16)1/2 = (17)1/2.
A fractional exponent means the denominator is used as a root, so this is √17.
Next, use the distance formula: distance = 
Thus, 
Square both sides: 17 = (2 – 1)2 + (6 – b)2. So, 17 = 1 + (6 – b)2. Subtract 1 from both sides to get 16 = (6 – b)2.
Take the square root of both sides to get 4 = 6 – b. Subtract 6 from both sides to find –2 = – b. So, b = 2.