Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Test 20 Grid Ins Questions with Answer Keys.
SAT 2022 Math Test 20 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
At a restaurant, each large order of fries has 350 more calories than one large soda. If 2 large orders of fries and 3 large sodas have a total of 1,500 calories, how many calories does one large order of fries have?
Show/Hide Answer Key
Correct Answer: 510
Algebra (rates) EASY
Let x represent the number of calories in a large order of fries because that is what the question is asking us to find. Since we are told that this is 350 calories more than the calories in a large soda, the number of calories in a large soda is x – 350. If 2 large fries and 3 large sodas have a total of 1,500 calories,
x + 3(x – 350) = 1,500
Distribute: 2x + 3x – 1,050 = 1,500
Simplify: 5x – 1,050 = 1,500
Add 1,050: 5x = 2,550
Divide by 5: x = 510
SAT Math Practice Online Test Question No 2:
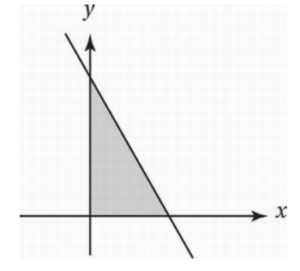
x ≥ 0
y ≥ 0
3x + y ≤ k
In the figure above, the shaded region represents the solution set for the system of inequalities shown. If the area of this shaded region is 24 square units, what is the value of k?
Show/Hide Answer Key
Correct Answer: 12
Additional topics (coordinate geometry) MEDIUM-HARD
The system of inequalities indicates that the line containing the hypotenuse of the triangle is given by the equation 3x + y = k, which has an x-intercept of (k/3, 0) and a y-intercept of (0, k). This means that the triangle has a base of k/3 and a height of k.

Simplify: k2/6 = 24
Multiply by 6: k2 = 144
Take the square root: k = 12
SAT Math Practice Online Test Question No 3:
If (cos x)(sin x) = 0.2, what is the value of (cos x + sin x)2?
Show/Hide Answer Key
Correct Answer: 1.4
Advanced Mathematics (trigonometry) MEDIUM-HARD
Recall the Pythagorean Trigonometric Identity, which is true for all x:
sin2 x + cos2 x = 1
Expression to be evaluated: (sin x + cos x)2
FOIL: (sin x + cos x)(sin x + cos x) = sin2 x + 2(sin x)(cos x) + cos2 x
Rearrange with Commutative and Associative Laws of Addition: 2(sin x)(cos x) + (sin2 x + cos2 x)
Substitute sin2 x + cos2 x = 1:
2(sin x)(cos x) + 1
Substitute (sin x)(cos x) = 0.2: 2(0.2) + 1 = 1.4
SAT Math Practice Online Test Question No 4:
Performance Banner Company creates promotional banners that include company logos. The Zypz Running Shoe Company would like a 4-foot high and 20-foot long banner that includes its logo, which has a height-to-length ratio of 5:8.
If the logo were scaled so that its height matched the height of the banner and then were placed in the center of the banner, then what would be the width, in feet, of each margin on either side of the logo?
Show/Hide Answer Key
Correct Answer: 6.8
Problem Solving (extended thinking) HARD
If the height of the logo is to match the height of the banner, it must have a height of 4 feet. Let x be the corresponding length of the logo. Since the logo has a height-to-length ratio of 5:8: 5/8 = 4/x
Cross multiply: 5x = 32
Divide by 5: x = 6.4
Since the banner is 20 feet long, there are 20 – 6.4 = 13.6 feet in total for the side margins. If the logo is centered, then each margin is half this length, 13.6 ÷ 2 = 6.8 feet.
SAT Math Practice Online Test Question No 5:
If 4 + √b = 7.2, what is the value of 4 – √b?
Show/Hide Answer Key
Correct Answer: 0.8 or 4/5
Algebra (radical equations) EASY
Given Equation: 4 + √b = 7.2
Subtract 4: √b = 3.2
Therefore, 4 – √b = 4 – 3.2 = 0.8
SAT Math Practice Online Test Question No 6:
In the xy-plane, the graph of the equation y = 3x2 – kx – 35 intersects the x-axis at (5, 0). What is the value of k?
Show/Hide Answer Key
Correct Answer: 8
Advance Mathematics (quadratics) EASY
Given Equation: y = 3x2 – kx – 35
Substitute x = 5 and y = 0: 0 = 3(5)2 – k(5) – 35
Simplify: 0 = 75 – 5k – 35
Simplify: 0 = 40 – 5k
Add 5k: 5k = 40
Divide by 5: k = 8
SAT Math Practice Online Test Question No 7:
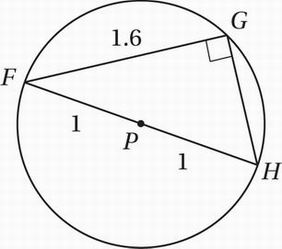
In the figure above, triangle FGH is inscribed in the circle with center P. If the area of the circle is π, what is the area of triangle FGH?
Show/Hide Answer Key
Correct Answer: 0.96
Additional Topics (circles/triangles) MEDIUM-HARD
When looking for the area of the triangle, remember that there are two basic methods: the direct method and the indirect method. With the direct method, we simply plug the base and height measurements into the formula A = bh/2, and with the indirect method, we find the area as the sum or difference of other areas. In this case, since we know the lengths of one of the sides, the direct method is probably best. But we will need to find the height as well.
Area of the circle is π: πr2 = π
Divide by π: r2 = 1
Take square root: r = 1
Now let’s mark up the diagram with this information. Since the radius of the circle is 1, the diameter FH has a length of 2. Now we can use the Pythagorean Theorem to find the length of GH, which is the height of the triangle if FG is taken as the base. (1.6)2 + (GH)2 = 22
Simplify: 2.56 + (GH)2 = 4
Subtract 2.56: (GH)2 = 1.44
Take square root: GH = 1.2
(Notice that this is in fact a 3-4-5 triangle: if we multiply 3-4-5 by 0.4, we get 1.2-1.6-2.)
Plug into area formula: A = bh/2 = (1.2)(1.6)/2 = 0.96
SAT Math Practice Online Test Question No 8:
If -3/5 < -2t + 1 < -3/7, what is one possible value of 6t?
Show/Hide Answer Key
Correct Answer: 4.29 ≤ x ≤ 4.79
Algebra (solving inequalities) HARD
-3/5 < -2t + 1 < -3/7
Multiply by -3 and “flip” inequalities: 9/5 > 6t – 3 > 9/7
Add 3: 24/5 > 6t > 30/7
Divide to get decimal form: 4.80 > 6t > 4.2857
Therefore any decimal value between 4.29 and 4.79, inclusive, is acceptable.
SAT Math Practice Online Test Question No 9:
If cos (x – π) = 0.4, what is the value of sin2 x?
Show/Hide Answer Key
Correct Answer: 0.84
Advanced Mathematics (trigonometry) MEDIUM-HARD
You may find it helpful to make a quick sketch of the unit circle on the xy-plane, as we discussed in Chapter 10. Subtracting π radians (or 180°) from an angle just means rotating the terminal ray of that angle 180° clockwise. It should be clear, then, that in the xy-plane, the angle with measure x – π points in the opposite direction of the angle with measure x. Recall that the cosine of an angle is just the x-coordinate of the point where its terminal ray intersects the unit circle. Since cos (x – π) = 0.4 (that is, its cosine is positive), its terminal ray must be in a quadrant where the x-coordinates are positive: either quadrant I or quadrant IV. Let’s just put it in quadrant I. This means that the angle with measure x is in quadrant III, and so it has the opposite cosine: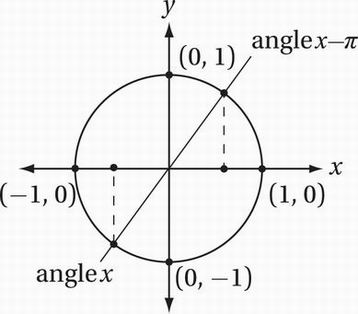
Recall Pythagorean Identity from Chapter 10: sin2 x + cos2 x = 1
Substitute cos x = 0.4: sin2 x + (-0.4)2 = 1
Simplify: sin2 x + 0.16 = 1
Subtract 0.16: sin2 x = 0.84
SAT Math Practice Online Test Question No 10:
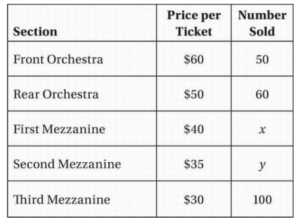
The table above shows information about the tickets sold for a recent performance by a theater troupe. The total revenue in ticket sales for this performance was $15,000.
If 15 more tickets were sold in the second mezzanine than in the first mezzanine, what is the total number of tickets that were sold for this performance?
Show/Hide Answer Key
Correct Answer: 371
Problem Solving (extended thinking) HARD
The total revenue from the tickets sold is $60(50) + $50(60) + $40x + $35y + $30(100). If the total revenue was $15,000, then 3,000 + 3,000 + 40x + 35x + 3,000 = 15,000
Subtract 9,000: 40x + 35y = 6,000
Divide by 5: 8x + 7y = 1,200
If 15 more tickets were sold in the second mezzanine than the first mezzanine: y = x + 15
Substitute y = x + 15 in previous equation: 8x + 7(x + 15) = 1,200
Distribute: 8x + 7x + 105 = 1,200
Subtract 105: 15x = 1,095
Divide by 15: x = 73
Substitute to find y: y = x + 15 = 73 + 15 = 88
Therefore, the total number of tickets sold is 50 + 60 + 73 + 88 + 100 = 371.