Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Mathematics Practice Test 46 Grid Ins Questions with Answer Keys | SAT Online Classes AMBiPi.
SAT 2022 Mathematics Practice Test 46 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
A rectangle of width 5 has a diagonal of length 13. What is the perimeter of the rectangle?
Show/Hide Answer Key
Correct Answer: 34
If a rectangle has a width of 5 and a diagonal of 13, this means that its other side must be 12, because 5:12:13 is a Pythagorean triple.
Therefore, the perimeter of the rectangle will be 5 + 12 + 5 + 12 = 34.
SAT Math Practice Online Test Question No 2:
If the distance from (2, 6) to (1, b) is a, a = (|-1| + 16)1/2, and b < a, what is the value of b?
Show/Hide Answer Key
Correct Answer: 2
Absolute value is the distance from zero to the number on the number line, or in other words, the positive version of the number.
So, (|-1| + 16)1/2 = (17)1/2. A fractional exponent means the denominator is used as a root, so this is √17.
Next, use the distance formula: distance = d=√((x2-x1)²+(y2-y1)²). Thus, √17 = √((2-1)²+(6-b)²)).
Square both sides: 17 = (2 – 1)2 + (6 – b)2. So, 17 = 1 + (6 – b)2. Subtract 1 from both sides to get 16 = (6 – b)2. Take the square root of both sides to get 4 = 6 – b. Subtract 6 from both sides to find –2 = – b. So, b = 2.
SAT Math Practice Online Test Question No 3:
If 3(y – 2) = 24, then what does 5(y – 2) equal?
Show/Hide Answer Key
Correct Answer: 40
Divide both sides of the equation by three to find that (y – 2) = 8.
There’s no need to find y since we need only to find five times the value of (y – 2). Multiply both sides of the equation to find that 5(y – 2) = 40.
SAT Math Practice Online Test Question No 4:
n = 12 x 2t/3.
The number of mice in a certain colony is shown by the formula above, such that n is the number of mice and t is the time, in months, since the start of the colony. If 2 years have passed since the start of the colony, how many mice does the colony contain now?
Show/Hide Answer Key
Correct Answer: 3072
Because the t in n = 12 x 2t/3 represents the number of months, we cannot use the 2 years time frame given in the question in place of t.
The colony has been growing for 24 months, which is evenly divisible by the 3 in the fractional exponent. The equation is much easier now that the fractional exponent is gone. n = 12 x 224/3 = 12 x 28 = 12 x 256 = 3,072.
SAT Math Practice Online Test Question No 5:
Squaring a certain number is equivalent to multiplying the number by 10 and then taking one-half the result. What is one possible value of the number?
Show/Hide Answer Key
Correct Answer: 0 or 5
Translate this word problem into math: x2 = 10x/2. Simplify to 2x2 = 10x, then x2 = 5x, and finally x = 5. There is another possibility: If x is replaced by 0 in the equation at any stage, it creates a true equation.
0 = 10(0)/2 = 0.
SAT Math Practice Online Test Question No 6:
On Thursday, Jeanine drove 20 miles to work, at an average speed of 40 miles per hour. She then drove home along the same route at an average speed of 50 miles per hour. How many hours did she spend driving to and from work on Thursday?
Show/Hide Answer Key
Correct Answer: 0.9
This is a rate question, so we can use the formula rate = distance/time.
Putting the information for Jeanine’s trip to work into this form gives 40 = 20/t. Isolate t to find that t = 20/t so t = 1/2.
Coming from work, Jeanine drives faster, so the rate is different, but the mileage is the same: 50 = 20/t, so t = 20/50 and t = 2/5.
Add the two together: 5/10 + 4/10 = 9/10
SAT Math Practice Online Test Question No 7:
If b is 9 more than c, c is 4 more than a, and d is 3 more than a, then what is the positive difference between b and d?
Show/Hide Answer Key
Correct Answer: 10
Here is another translation problem. The first sentence can be translated to b = c + 9, the second sentence as c = a + 4, the third sentence as d = a + 3. The question at the end is really asking for the value of b – d.
Plug in a value for a in the third equation and it will give the value of d that we need. If a = 2, then d = 2 + 3 = 5. Use the same value for a in the second equation to find a value for c: c = 2 + 4, so c = 6.
Plug this into the first equation to get the b value we need in order to find b – d. b = 6 + 9 = 15, so b – d = 15 – 5 = 10.
SAT Math Practice Online Test Question No 8:
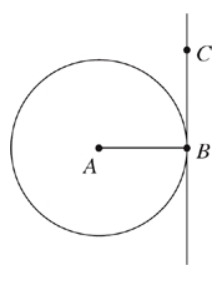
In the figure above, BC is tangent to circle with center A at B. If the length of AC (not shown) is 10√3, and AC = 2AB, what is the length of BC?
Show/Hide Answer Key
Correct Answer: 15
A line that is tangent to a circle forms a 90° angle with a radius or diameter. Radius AB and line BC form the legs of right triangle ABC, and the hypotenuse is AC. We know that AC = 10√3, and that AB = AC/2, or one half of AC, so AB = 5√3.
When the hypotenuse is twice the length of the shortest side, we have a 30-60-90 triangle. The ratio of this special right triangle x : x√3 : 2x, where x is the length of the side opposite the 30° angle. So BC = 5√3 x √3 = 5 x 3 = 15.
SAT Math Practice Online Test Question No 9:
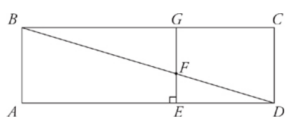
In the figure above, the area of rectangle ABCD is 120. If AD ⟂ EG, CD = 6, and AE = 12, what is the length of EF?
Show/Hide Answer Key
Correct Answer: 2.4
Write the information from the question onto the figure given:
CD = 6, so AB = 6 because ABCD is a rectangle. Since the area of the rectangle is 120, we can find the length by using what we know in the area formula.
Area = lw, so 120 = l(6), and 20 = l. Side AD = 20, and we know that AE = 12, so ED must equal 8. Now we have enough information to find the length of EF.
The perpendicular EG means that triangle ABD and triangle EFD are similar, so their sides are in proportion to each other: 6/20 = EF/8, so 20 × EF = 48, and EF = 2.4 or 12/5.
SAT Math Practice Online Test Question No 10:
Set X consists of 12 numbers. The average (arithmetic mean) of the first 6 numbers is 15. The sum of the last six numbers is 24. What is the average of all 12 numbers in set X?
Show/Hide Answer Key
Correct Answer: 9.5
Use an average pie every time the question uses the word average. In this case we end up with the following average pies that use the information in the question:
We need an average pie for the first six numbers. The six numbers’ average is 15, so the total of those six numbers is 15 × 6 = 90. The last six have an average of 4, so the total of those six numbers is 4 × 6 = 24.
Now take the two totals and add them together for the final mention of the word average. The total for all 12 numbers is 114, so to find the average, divide 114 by 12, which gives 9.5. You could also reduce the fraction 114/12, since numerator and denominator are both divisible by 6, to 19/2.