Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Prep Course 47 Grid Ins Questions with Answer Keys | SAT Online Course AMBiPi.
SAT 2022 Math Prep Course 47 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
If √x + 22 = 38, x =
Show/Hide Answer Key
Correct Answer: 256
To solve this equation, get √x by itself. √x = 16, so square both sides: (√x)² = 16², so x = 256.
SAT Math Practice Online Test Question No 2:
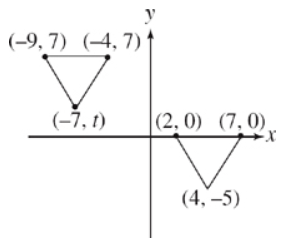
In the figure above, the two triangles have the same area. What is the value of t?
Show/Hide Answer Key
Correct Answer: 2
Because the two triangles have the same area and each has a base with a length of 5, their heights must be equal as well.
For a triangle, Area = [1/2]bh. The bottom triangle has a height of 5 because the base is on the x-axis and the tip is at –5. This means that t = 7 – 5 = 2.
SAT Math Practice Online Test Question No 3:
Set A contains all odd integers from 0 to 10 that are not prime. If y is a member of set A, what is one possible value of y?
Show/Hide Answer Key
Correct Answer: 1 or 9
List the numbers described: All the odd integers from 0 to 10 are 1, 3, 5, 7, 9. Of these numbers, 3, 5, and 7 are prime, leaving only 1 or 9.
SAT Math Practice Online Test Question No 4:
If q is an integer between 50 and 70 and can be expressed as 7j + 3 where j is an integer, what is one possible value of q?
Show/Hide Answer Key
Correct Answer: 52, 59 or 66
One way to solve this problem is to plug in numbers for j until you get a result that is between 50 and 70.
Another way is to list the multiples of 7 that are close to the range given, such as 49, 56, and 63, and add 3 to each one, which gives 52, 59, and 66 respectively.
Any one of these three numbers will get you the credit for the question. You need to come up with only one possible value.
SAT Math Practice Online Test Question No 5:
Nine people in an investment club purchased $114 worth of stock x. Each of five people bought a share of stock x. Each of the three people bought 4/5 of a share. One person bought 1/5 of a share. How much did a share of stock x cost?
Show/Hide Answer Key
Correct Answer: 15
We need to find the cost of a single share of stock x. Of the nine people, 5 bought a share each, so if cost = c, then that is 5c. There are also 3 people who each bought 4/5 of a share, so that’s 3[(4/5)c].
There is one more person, who bought 1/5 of a share. Since the club spent $114, we can create the equation:
5c + 3[(4/5)c] + 1[(1/5)c] = 114. This simplifies to [25/5]c + [12/5]c + [1/5]c = [38/5]c = 114.
Multiply both sides by 5/38 to get c by itself, and c = 114[5/38] = 15.
SAT Math Practice Online Test Question No 6:
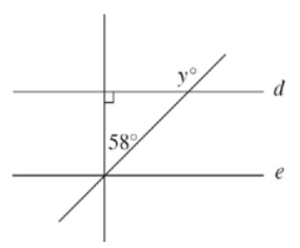
In the figure above, if d is parallel to e, what is the value of y?
Show/Hide Answer Key
Correct Answer: 148
Use Fred’s Theorem: A-line crossing two parallel lines creates big angles and small angles. The big angle that matches y is split by a line perpendicular to d and e. The big angle is 58 + 90 = 148, which is also the value for y.
Another way to solve this is to find the third angle of the triangle: 180 – 90 – 58 = 32. The 32° angle and the y° angle make up a straight line, so 180 – 32 = 148.
SAT Math Practice Online Test Question No 7:
If 4x · n2 = 4x+1 · n and x and n are both positive integers, what is the value of n?
Show/Hide Answer Key
Correct Answer: 4
First simplify the equation 4x ? n2 = 4x+1 ? n, to 4x ? n = 4x+1, then plug in.
If x = 2, then 42 ? n = 42+1. Since 16n = 43, then 16n = 64 and n = 4.
SAT Math Practice Online Test Question No 8:
The graph above shows the foreign languages studied by 500 students during the 1996–1997 academic year. At the beginning of the 1997–1998 academic year, the number of students studying a foreign language increased by 20, and the same number of students studied Spanish, Latin, and German as did during the previous year. If the percentage of students who studied Japanese increased to 10% during the 1997–1998 academic year, how many students studied French that year? (Assume that no student studied more than one foreign language at a time.)
Show/Hide Answer Key
Correct Answer: 118
Based on the numbers for the 1996–1997 academic year and the percents shown in the graph, the 500 students are broken down into the following groups:
Spanish = [40/100]500 = 200
French = [25/100]500 = 125
Latin = [20/100]500 = 100
Japanese = [5/100]500 = 25
German = [10/100]500 = 50
In the 1997–1998 school year, there were 20 more students, for a total of 520. The percent of students studying Japanese is now 10% of this, so there are 52 Japanese students and the same number of Spanish, Latin and German students as in the previous year. The number of French students (f) is the only unknown now: 520 = (52 + 200 + 100 + 50) + f , and 520 = 402 + f, so f = 118.
SAT Math Practice Online Test Question No 9:
If [x2 + 108]/9 and f(3a) = -7a, then what is the product of all possible real values of a?
Show/Hide Answer Key
Correct Answer: 12
Plug in the value we are given for x into the function.
[(3a)2 + 108]/9 = -7a.
Now we can solve for all possible values of a as the question asks: [9a2 + 108]/9 = -7a, and the fraction can be further simplified : [9(a2 + 12)]/9 = a2 + 12.
Since a2 + 12 = –7a can be rearranged into a quadratic equation, we can find two possible values for a: a2 + 7a + 12 = 0, so (a + 3)(a + 4) = 0, and a can either be –3 or –4.
The answer is 12 because we need the product of the possible answers and (–3)(–4) = 12.
SAT Math Practice Online Test Question No 10:
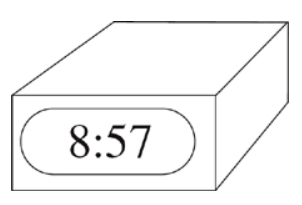
The 12-hour digital clock above shows one example of a time at which the sum of the digits representing the time is equal to 20. During a 12-hour period, starting at noon, for how many minutes would the sum of the digits displayed be greater than or equal to 20 ?
Show/Hide Answer Key
Correct Answer: 20
This is a pattern question in disguise: Write it out, and be methodical! For the four spaces for digits, the first can be only 1, the second could be any digit 0 through 9, the third can be only 0 through 5, and the last digit can be any digit 0 through 9.
When the last two spaces have the highest possible digits, showing :59, if the hour is 5 or below, the total is less than 19. This includes the hour of 12, because the hour does not count as 12, it is 1 + 2 = 3. In the next hour, the digits in 6:59 add to 20.
In the next hour, the digits in 7:59 add up to 21. If the middle digit is one less, 7:49 adds up to 20. If instead the last digit was one less, 7:58 also adds up to 20. In the 8 o’clock hour, we have, 8:39, 8:48, 8:49, 8:57, 8:58, and 8:59.
In the 9 o’clock hour we have 9:29, 9:38, 9:39, 9:47, 9:48, 9:49, 9:56, 9:57, 9:58, and 9:59. There will be none in the 10 or 11 o’clock hours because their hour digits add up to 1 and 2 respectively and are too small.
Count up the times that work: There are a total of 20 times during the 12 hours that add up to 20 or more.