Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Practice Problems Test 17 Grid Ins Math Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Practice Problems Test 17 Grid Ins Math Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
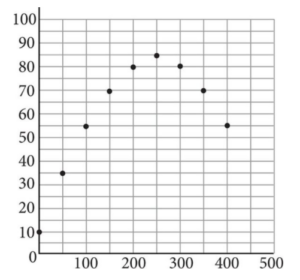
Nine data points were used to generate the scatterplot shown above. Assuming all whole number values for the data points, what is the maximum value in the range of the data?
Show/Hide Answer Key
Correct Answer: 85
To find the maximum value in the range of the data, look for the highest point on the graph, which is (250, 85). The y-value is 85, so 85 is the maximum value in the range.
SAT Math Practice Online Test Question No 2:
If Ax + By = C is the standard form of the line that passes through the points (–4, 1) and (3, –2), where A is an integer greater than 1, what is the value of B?
Show/Hide Answer Key
Correct Answer: 7
Use the given points, (–4, 1) and (3, –2) , and the slope formula to find m:
m = (y2 – y1)/(x2 – x1) = (-2 – 1)/3 -(-4) = -3/7
Next, find the y-intercept, b, using the slope and one of the points:
y = (-3/7)x + b
1 = (-3/7)(-4) + b
1 = 12/7 + b
-5/7 = b
Write the equation in slope-intercept form:
y = (-3/7)x – 5/7.
Now, rewrite the equation in the form Ax + By = C, making sure that A is a positive integer (a whole number greater than 0):
y = (-3/7)x – 5/7.
(3/7)x + y = (-5/7)
7[(3/7 + y) = (-5/7)]7
3x + 7y = -5
The question asks for the value of B (the coefficient of y), so the correct answer is 7.
SAT Math Practice Online Test Question No 3:
If -3/2 < 3 – a/5 < -1/4, what is the maximum possible whole number value of a?
Show/Hide Answer Key
Correct Answer: 22
20(-3/2) < 20(3 – a/5) < 20(-1/4)
-30 < 60 – 4a < -5
-30 – 60 < 60 – 60 – 4a < -5 – 60
-90 < -4a < -65
-90/-4 > -4a/-4 > -65/-4
22.5 > a > 16.25
16.25 < a < 22.5
The question asks for the maximum possible whole number value of a, so the correct answer is 22.
SAT Math Practice Online Test Question No 4:
Medically speaking, remission is a period in which the symptoms of a disease or condition subside or, for some diseases, a period during which the condition stops spreading or worsening. In a certain drug trial in which a drug designed to treat cancer was tested, exactly 48% of patients experienced remission while take the drug. What is the fewest number of patients who could have participated in this trial?
Show/Hide Answer Key
Correct Answer: 25
Every percent can be written as a number over 100 (because per cent means per hundred), so start by writing 48% as a fraction and reducing it: 48/100 = 12/25. The denominator of this fraction (25) gives the least possible number of patients who could have participated in the trial because it is the first number that will cancel when multiplied by the fraction.
SAT Math Practice Online Test Question No 5:
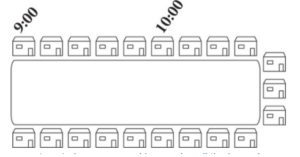
Daniel works for a pest control company and is spraying all the lawns in a neighborhood. The figure above shows the layout of the neighborhood and the times that Daniel started spraying the lawns at two of the houses. Each lawn in the neighborhood is approximately 0.2 acres in size and takes the same amount of time to spray.
How many minutes will it take Daniel to spray all of the lawns in the neighborhood?
Show/Hide Answer Key
Correct Answer: 252
According to the figure, he started the first house at 9:00 and the sixth house at 10:00, so it took him 1 hour, or 60 minutes, to spray 5 houses. This gives a unit rate of 60 ÷ 5 = 12 minutes per house. Count the houses in the figure—there are 21. Multiply the unit rate by the number of houses to get 12 × 21 = 252 minutes to spray all the lawns.
SAT Math Practice Online Test Question No 6:
If 5/x – 2/5 = 1, what is the value of x?
Show/Hide Answer Key
Correct Answer: 25/7 or 3.57
5/x – 2/5 = 1
Add 2/5 and Simplify:
5/x = 1 + 2/5
5/x = 7/5
Cross Multiply: 25 = 7x
Divide by 7: 25/7 = x
SAT Math Practice Online Test Question No 7:
If x represents the radian measure of an angle, where 0 ≤ x ≤ π/2, and x = 5/13, then what is the value of (π/2 – x)?
Show/Hide Answer Key
Correct Answer: 2.4
Since x represents the radian measure of an acute angle, and sin x = 5/13, we can use the definition of sine (=O/H) to draw a right triangle:
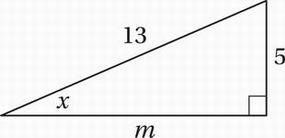
We might notice that this is a 5-12-13 special right triangle, or simply use the Pythagorean Theorem to show that m = 12. We can also show that the other acute angle in the triangle must be complementary to x (that is, together they form a right angle), and so must have a measure of (π/2 – x).
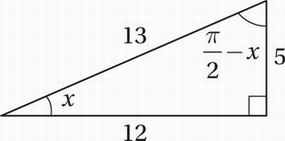
To find tan(π/2 – x),we simply have to use the angle with measure (π/2 – x) as our new reference angle, and use TOA:
tan(π/2 – x) = 12/5 = 2.4
SAT Math Practice Online Test Question No 8:
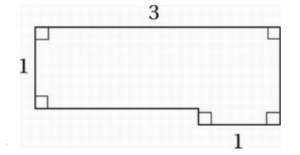
If the area of the figure above is 16/5 square units, what is its perimeter?
Show/Hide Answer Key
Correct Answer: 8/4 or 42/5

First, drawing a line as shown in the diagram shows that the figure is composed of two rectangles, but the height of the smaller one is unknown. Let’s call it x. The area of the larger rectangle is (3)(1) = 3, and the area of the smaller rectangle is (1)(x) = x. Clearly, the area of the figure must be the sum of these two areas:
Area = 16/5 = 3+ x
Subtract 3: 16/5 – 3 = 16/5 – 15/5 = 1/5 = x
Therefore, the perimeter of the figure is just the sum of the lengths of its sides. If we travel around the figure clockwise from the leftmost side, we get a perimeter of 1 + 3 + 1 + 1/5 + 1 + 1/5 + 2 = 8 + 2/5 = 8.4
SAT Math Practice Online Test Question No 9:
In a writer’s workshop, there are half as many men as women. If there are 24 total men and women in the writer’s workshop, how many men are there?
Show/Hide Answer Key
Correct Answer: 8
Let x equal the number of men in the workshop. If there are half as many men as women, there must be 2x women in the workshop, or a total of x + 2x = 3x men and women in the workshop. Since this total equals 24: 3x = 24
Divide by 3: x = 8
As with all algebra problems, make sure you confirm that the value you’ve solved for is the value the question is asking for. Since x is in fact the number of men, it is the final answer.
SAT Math Practice Online Test Question No 10:
The square of a positive number is 0.24 greater than the number itself. What is the number?
Show/Hide Answer Key
Correct Answer: 1.2 or 6/5
First, translate the given fact into an equation.
The square of a positive number is 0.24 greater than the number itself: x2 = x + 0.24
Subtract x and 0.24: x2 – x – 0.24 = 0
Multiply by 100 to eliminate the decimal: 100x2 – 100x – 24 = 0
Now we factor using Product-Sum Method. Remember that the product number is ac = (100)(-24) = -2,400, and the sum number is b = -100. The two numbers with a sum of -100 and a product of -2,400 are 20 and -120.
Expand middle term using -100 = 20 – 120: 100x2 + 20x – 120x – 24 = 0
Factor by grouping in pairs: 20x(5x + 1) – 24(5x + 1) = 0
Take out common factor: (5x + 1)(20x – 24) = 0
Using the Zero Product Property, we see that x = -1/5 or x = 24/20 = 6/5. Since we are told that x is a positive number, x = 6/5 or 1.2.



