Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Test Prep 34 Grid Ins Questions with Answer Keys | SAT Online Classes AMBiPi.
SAT 2022 Math Test Prep 34 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
In a school survey, 40% of all students chose history as their favorite subject; 25% chose English, and 14 chose some other subject as their favorite. How many students were surveyed?
Show/Hide Answer Key
Correct Answer: 40
Sixty-five percent chose history or English, leaving 35 percent for other subjects. This 35 percent represents 14 students, so you’re basically being asked, “35 percent of what number is 14?” You can use the is/of the method to solve this problem:
14/x = 35/100, 35x = 1,400, x = 40
The is/of the method relies on this formula: is/of = %/100.
SAT Math Practice Online Test Question No 2:
The ratio of a rectangle’s width to its length is 2:5. If its perimeter is 84 feet, find its width, in feet.
Show/Hide Answer Key
Correct Answer: 12
When a question tells you the ratio of unknown quantities, you can simply tack an x onto the end of each number. Thus, the length of the rectangle is 5x and the width is 2x. Now you may want to draw and label a rectangle to help you solve this problem:
Don’t fall into the trap of writing 2x + 5x = 84; a rectangle has four sides, not two. Write either 2x + 5x + 2x + 5x = 84 or 2(2x + 5x) = 84. Either way, the left side is 14x, so 14x = 84, and x = 6.
Another trap lurks here: 6 isn’t the answer. You represented the width with 2x in your original equation, so the width is 2(6) = 12 feet.
SAT Math Practice Online Test Question No 3:
Don’t fall into the trap of writing 2x + 5x = 84; a rectangle has four sides, not two. Write either 2x + 5x + 2x + 5x = 84 or 2(2x + 5x) = 84. Either way, the left side is 14x, so 14x = 84, and x = 6. Another trap lurks here: 6 isn’t the answer. You represented the width with 2x in your original equation, so the width is 2(6) = 12 feet.
Show/Hide Answer Key
Correct Answer: 6
Although you can use trial and error to answer this question, I use algebra here to give you a little more practice.
Darren makes $9 an hour on weekdays, and 11? 2 × $9 = $13.50 on weekends. If you let d equal his weekday hours and e equal his weekend hours, you know that $9(d) + $13.50(e) = $189.00.
You also know that d + e = 18 (his total hours), so you can?solve this problem using substitution: d = 18 – e, so $9(18 – e) + $13.50e = $189. Distributing: $162 – $9e + $13.50e= $189.
Combining like terms, you get $162 + $4.50e= $189. Now just subtract 162 from both sides and divide by 4.50, to get e = 6. Simple, right?
SAT Math Practice Online Test Question No 4:
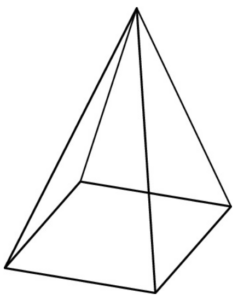
The pyramid above has a square base of a length of 10 cm and a height of 12 cm. Determine the total surface area of all five faces, in square centimeters.
Show/Hide Answer Key
Correct Answer: 360
The total surface area is the sum of the area of the square and the area of the four triangles. The area of the square is easy to find: It’s simply 10 × 10 = 100.
The triangles are a little tougher. They don’t have a height of 12 because 12 is the height of the pyramid, but the triangles are slanted. However, if you look at the following diagram, you see that you can find the height of the slanted triangles by using the Pythagorean Theorem.
The little triangle in the diagram is a right triangle.
One leg is 12 (the height of the pyramid). The second leg is half the width of the square, or 5. This triangle is actually the world’s second-most famous right triangle, the 5-12-13 triangle. (If you didn’t remember this little tidbit, you could’ve figured it out with the Pythagorean Theorem.)
The hypotenuse, 13, is the altitude of each of the tilted triangles that make up the sides of the pyramid. Because the triangle’s area is 1? 2 × base × height, each triangle’s area is 1? 2 × 10 × 13 = 65.
The four triangles together have an area of 4 × 65 = 260. Adding in the 100 from the base gives you 360, which is the answer.
SAT Math Practice Online Test Question No 5:
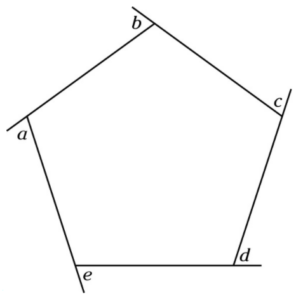
In this regular pentagon, find the sum, in degrees, of the angles a, b, c, d, and e.
Show/Hide Answer Key
Correct Answer: 360
This is an old semi-trick question: In any shape, the sum of the exterior angles is always 360 degrees.
SAT Math Practice Online Test Question No 6:
Find a solution to the equation p2 = 3p + 40.
Show/Hide Answer Key
Correct Answer: 8
Although you may be able to get the answer by trial and error, this problem is really begging to be factored in.
To factor a quadratic equation (that is, an equation with something “squared” in it), you must first set the equation equal to zero. Making the squared term negative is never a good idea, so you should solve it as follows:
p² = 3p + 40
-3p – 3p
p² – 3p = 40
-40 – 40
p² – 3p – 40 = 0
This equation factors out to (p – 8)(p + 5) = 0. It has two solutions: p = 8 and p = –5. Because you can’t grid a negative answer, you have to go with 8.
SAT Math Practice Online Test Question No 7:
If all the integers from 1 to 2,010 inclusive were written down, how many total digits would appear?
Show/Hide Answer Key
Correct Answer: 6933
Wow, that’s a lot of numbers. They come into the following four groups:
One-digit numbers: 1 to 9, for 9 × 1 = 9 digits
Two-digit numbers: 10 to 99, for 90 × 2 = 180 digits (Did you remember the formula to count the numbers? It’s 99 – 10 + 1 = 90.)
Three-digit numbers: 100 to 999, for 900 × 3 = 2,700 digits
Four-digit numbers: 1,000 to 2,010, for 1,011 × 4 = 4,044 digits
Your total is 9 + 180 + 2,700 + 4,044 = 6,933.
SAT Math Practice Online Test Question No 8:
The shortest side of triangle T is 10 cm long, and triangle T‘s area is 84 cm2. Triangle U is similar to triangle T, and the shortest side of triangle U is 15 cm long. Find the area of triangle U in cm2.
Show/Hide Answer Key
Correct Answer: 189
You don’t really need a diagram to solve this one, but I include one out of habit, anyway:
The sides of triangle U are 11? 2 times bigger than the sides of triangle T (because 15 ÷ 10 = 11? 2). Now you need to remember an obscure (but important-on-the-SAT) fact: The ratio of the areas of similar figures is the square of the ratio of their sides because the area of a triangle is 1? 2 × base × height and both the base and the height are 11? 2 times bigger.
So the area is 11?2 × 11?2 = 21?4 times bigger. And 84 cm² × 21?4 = 189 cm².
SAT Math Practice Online Test Question No 9:
The height of an object thrown in the air with an initial velocity of 96 feet per second can be modeled by the function h(t) = -16t2 + 96t, where h is in feet and t is in seconds. What would be the ball’s maximum height, in feet?
Show/Hide Answer Key
Correct Answer: 144
When I took the SAT, graphing calculators weren’t in existence, so I had to work this one out by hand. Luckily, times have changed, and you can just plug the numbers into your calculator to find the answer.
If you don’t have such a magical device, rely on the formula that says the vertex of a parabola occurs at x = -b/2a, where b is the x-coefficient and a is the x²-coefficient (although here you’re using t, not x).
Plugging in here tells you that the vertex occurs when t = -(96)/2(-16) = 3, and plugging this result into the original equation gives you h = 144.
SAT Math Practice Online Test Question No 10:
The pie graph above shows the percentage of students who take each foreign language at a certain high school. If 260 students take either French or Spanish, how many students go to school?
Show/Hide Answer Key
Correct Answer: 400
The graph tells you that 65% of the students take either French or Spanish, so you can use the old is-of formula: is/of = %/100.
Here, the number you know, 260, is 65% of the number you’re looking for, so you can write 260/x = 65/100. Cross-multiplying gives you 65x = 26,000, and, thankfully, 65 goes into 26,000 a nice, even 400 times.