Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Practice Test 40 Grid Ins Questions with Answer Keys | SAT Online Classes AMBiPi.
SAT 2022 Practice Test 40 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
A, B, C, D
How many different three-letter arrangements of the letters above are possible if no letter may be repeated? (An arrangement like ABC is distinct from an arrangement like BCA.)
Show/Hide Answer Key
Correct Answer: 24
This is a “counting” problem, so it helps to know the fundamental counting principle. Since you are making a three-letter arrangement, there are three decisions to be made.
The number of choices for the first letter is four; then there are three letters left for the second spot, then two left for the third spot. This gives a total of 4 x 3 x 2 = 24 possible arrangements.
SAT Math Practice Online Test Question No 2:
Admission to a museum is $10 for each adult and $5 for each child. If a group of 30 people pays a total of $175 in admission, how many adults are in the group?
Show/Hide Answer Key
Correct Answer: 5
If there are a adults, there must be 30 – a children, because the total number of people is 30.
Therefore: 10a + 5(30 – a) = 175
Distribute: 10a + 150 – 5a = 175
Simplify: 5a + 150 = 175
Subtract 150: 5a = 25
Divide by 5: a = 5
SAT Math Practice Online Test Question No 3:
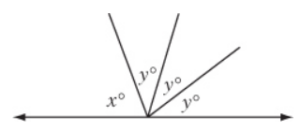
In the figure above, if x = 2y, then what is the value of y?
Show/Hide Answer Key
Correct Answer: 36
There are 180° on one side of a line: 2y + y + y + y = 180°
Combine like terms: 5y = 180°
Divide by 5: y = 36°
SAT Math Practice Online Test Question No 4:
In the xy-plane, the line mx – 3y = 21 passes through the point (3,5). What is the value of m?
Show/Hide Answer Key
Correct Answer: 12
Just substitute x = 3 and y = 5 into the equation and solve for m:
3m – 15 = 21
Add 15: 3m = 36
Divide by 3: m = 12
SAT Math Practice Online Test Question No 5:
If, for some constant value b, the equation y = |2x – b| is satisfied by the point (5, 2), then what is one possible value of b?
Show/Hide Answer Key
Correct Answer: 8 or 12
y = |2x – b|
Plug in (5,2): 2 = |2(5) – b|
Simplify: 2 = |10 – b|
(10 – b) = 2 or (10 – b) = -2
Subtract 10: -b = -8 or -b = -12
Multiply by -1: b = 8 or b = 12
SAT Math Practice Online Test Question No 6:
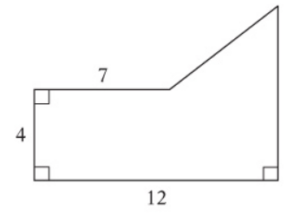
The area of the figure above is 78. What is its perimeter?
Show/Hide Answer Key
Correct Answer: 52
Break a shape like this into recognizable four-sided figures and triangles that are easier to deal with.
The area of the rectangle on the left is 7 x 4 = 28. The area of the rectangle on the right is 5 x 4 = 20.
The sum of those two areas is 28 + 20 = 48. The area remaining for the triangle is the difference of 78 – 48 = 30.
Set up an equation for the area of a triangle to solve for x: Area = 1/2(base)(height)
30 = 1/2(5)(height)
Divide by 1/2: 60 = 5(height)
Divide by 5: 12 = height
To find the hypotenuse of the right triangle, set up the Pythagorean theorem and solve 5² + 12² = c²
25 + 144 = c²
169 = c²
c = 13

To find the perimeter of the figure, add up all of the sides: 13 + 12 + 4 + 5 + 7 + 4 + 7 = 52
SAT Math Practice Online Test Question No 7:
For all real numbers n, let n be defined by n2/16. What is the value of 42?
Show/Hide Answer Key
Correct Answer: 1
n = n²/16
If it helps, you can think of this as f(n) = n²/16. Find the value of [f(4)]²
Plug in 4 for n: f(4) = 4²/16 = 16/16 = 1
Plug in 1 for f(4): [(f(4)]² = (1)² = 1
SAT Math Practice Online Test Question No 8:
If the sum of two numbers is 4 and their difference is 2, what is their product?
Show/Hide Answer Key
Correct Answer: 3
Set up equations: x + y = 4
x – y = 2
Add straight down: 2x = 6
Divide by 2: x = 3
Plug in 3 for x: 3 + y = 4
Subtract 3: y = 1
Final product: (x)(y) = (3)(1) = 3
SAT Math Practice Online Test Question No 9:
Points P, Q, R, and S lie on a line in that order. If PS is twice as long as PR and four times as long PQ, what is the value of QS/PQ?
Show/Hide Answer Key
Correct Answer: 3
Draw a line with points P, Q, R, and S on the line in that order.
You are given that PS = 2 PR and that PS = 4PQ, so choose values for those lengths, like PS = 12, PR = 6, and PQ = 3.

SAT Math Practice Online Test Question No 10:
If the sum of five consecutive even integers is 110, what is the least of these integers?
Show/Hide Answer Key
Correct Answer: 18
Since these numbers are “evenly spaced,” their mean (average) is equal to their median (middle number). The average is easy to calculate: 110/5 = 22.
Therefore, the middle number is 22, so the numbers are 18, 20, 22, 24, and 26.
Alternatively, you can set up an equation to find the sum of five consecutive unknown even integers, where x is the least of these:
x + (x + 2) + (x + 4) + (x + 6) + (x + 8) = 110
Combine like terms: 5x + 20 = 110
Subtract 20: 5x = 90
Divide by 5: x = 18
So the five integers are 18, 20, 22, 24, and 26.