Welcome to AMBiPi (Read as: एम्बीपाई) (Amans Maths Blogs). JEE Mains and JEE Advanced exams are the engineering entrance exams for taking admission in IITs, NITs and other engineering colleges. In this article, you will get JEE Main Mathematics Previous Paper Complex Numbers Questions Answer Keys Solutions.
JEE Mains Mathematics Complex Numbers Questions Bank
Complex Numbers Problems for Class 12 JEE Questions No: 31
A value of θ for which (2 + 3isinθ) / (1 – 2isinθ) is purely imaginary, is
[2016]
Option A: π/6
Option B: sin-1(√3/4)
Option C: sin-1(1/√3)
Option D: π/3
Show/Hide Answer Key
Option C: sin-1(1/√3)
JEE Complex Numbers Questions No: 32
The point represented by (2 + i) in Argand plane moves 1 unit eastwards, then 2 units northwards and finally from there 2√2 units in the south-westwards direction. Then its new position in the Argand plane is at the point represented by
[2016]
Option A: 1 + i
Option B: 2 + 2i
Option C: -2 – 2i
Option D: -1 – i
Show/Hide Answer Key
Option A: 1 + i
JEE Main Complex Numbers Questions No: 34
Let ω be a complex number such that 2ω + 1 = z where z = √-3, if

, then k is equal to
[2017]
Option A: -z
Option B: z
Option C: -1
Option D: 1
Show/Hide Answer Key
Option A: -z
JEE Mathematics Complex Numbers Questions No: 34
If α, β ∈ C are the distinct roots of the equation x2 – x + 1 = 0, then α107 + β107 is equal to
[2018]
Option A: 2
Option B: -1
Option C: 0
Option D: 1
Show/Hide Answer Key
Option D: 1
JEE Main Math Complex Numbers Questions No: 35
The least positive integer n for which [(1 + i√3) / (1 – i√3)]n = 1, is
[2018]
Option A: 2
Option B: 6
Option C: 5
Option D: 3
Show/Hide Answer Key
Option D: 3
Complex Numbers JEE Questions No: 36
The set of all α ∈ R for which ω = (1 + (1 – 8)α)z is a purely imaginary number, for all z ∈ C satisfying |z| = 1 and Re(z) ≠ 1 is
[2018]
Option A: {0}
Option B: an empty set
Option C: {0, 1/4, -1/4}
Option D: equal to R
Show/Hide Answer Key
Option A: {0}
Complex Numbers JEE Main Questions No: 37
Let A = {θ ∈ (-π/2, π) : (3 + 2isinθ) / (1 – 2isinθ) is purely imaginary}. Then, the sum of the elements in A is
[2019]
Option A: 5π/6
Option B: π
Option C: 3π/4
Option D: 2π/3
Show/Hide Answer Key
Option D: 2π/3
Complex Numbers Questions for JEE Mains Questions No: 38
Let z = (√3/2 + i/2)5 + (√3/2 – i/2)5. If Re(z) and Im(z) respectively denote the real and imaginary parts of z, then
[2019]
Option A: Im(z) = 0
Option B: Re(z) > 0 and Im(z) > 0
Option C: Re(z) < 0 and Im(z) > 0
Option D: Re(z) = -c
Show/Hide Answer Key
Option A: Im(z) = 0
Complex Numbers Questions and Answers No: 39
Let (-2 – i/3)3 = (x + iy) / 27, where x and y are real numbers then y – x equals
[2019]
Option A: 91
Option B: -85
Option C: 85
Option D: -91
Show/Hide Answer Key
Option A: 91
Complex Numbers Questions with Solutions No: 40
If z = (√3/2 + i/2), then (1 + iz + z5 + iz8)9 equal to
[2019]
Option A: 0
Option B: 1
Option C: (-1 + 2i)9
Option D: -1
Show/Hide Answer Key
Option D: -1
JEE Mains Complex Numbers Questions No: 41
Let z ∈ C be such that |z| < 1. If ω = (5 + 3z) / 5(1 – z), then
[2019]
Option A: 5Re(ω) > 4
Option B: 4Im(ω) > 4
Option C: 5Re(ω) > 1
Option D: 5Im(ω) < 1
Show/Hide Answer Key
Option C: 5Re(ω) > 1
JEE Mains Math Complex Numbers Questions No: 42
If z and ω are two complex numbers such that |zω| = 1 and arg(z) – arg(ω) = π/2, then
[2019]
Option A: zω = i
Option B: zω = (-1 + i) / √2
Option C: zω = -i
Option D: zω = (1 – i) / √2
Show/Hide Answer Key
Option C: zω = -i
Complex Numbers Questions for JEE Questions No: 43
Let z1 and z2 be any two non-zero complex numbers such that 3|z1| = 4|z2|. If z = 3z1/2z2 + 2z2/3z1, then
[2019]
Option A: Re(z) = 0
Option B: |z| = √(5/2)
Option C: |z| = (1/2)√(17/2)
Option D: Im(z) = 0
Show/Hide Answer Key
Option
Complex Numbers Problems for Class 11 Questions No: 44
Let z be a complex number such that |z| + z = 3 + i, where i = √-1. Then |z| is equal to
[2019]
Option A: √34 / 3
Option B: 5/3
Option C: √41 / 4
Option D: 5 / 4
Show/Hide Answer Key
Option B: 5/3
Complex Numbers Problems for Class 12 Questions No: 45
Let z1 and z2 be two complex numbers satisfying |z1| = 9 and |z2| – |3| – |4i| = |4|. Then, the minimum value of |z1 – z2| is
[2019]
Option A: 0
Option B: √2
Option C: 1
Option D: 2
Show/Hide Answer Key
Option A: 0
Complex Numbers Problems for Class 11 JEE Questions No: 46
If (z – α) / (z + α) (α ∈ R) is purely imaginary number and |z| = 2, then a value of α is
[2019]
Option A: 2
Option B: 1
Option C: 1/2
Option D: √2
Show/Hide Answer Key
Option A: 2
Complex Numbers Problems for Class 12 JEE Questions No: 47
If a > 0 and z = (1 + i)2 / (a – i), has magnitude √2/5, then z is equal to
[2019]
Option A: -1/5 – 3i/5
Option B: -3/5 – i/5
Option C: 1/5 – 3i/5
Option D: -1/5 + 3i/5
Show/Hide Answer Key
Option A: -1/5 – 3i/5
JEE Complex Numbers Questions No: 48
Let z ∈ C with Im(z) = 10 and it satisfies (2z – n) / (2z + n) = 2i – 1 for some natural number n. Then,
[2019]
Option A: n = 20 and Re(z) = -10
Option B: n = 40 and Re(z) = 10
Option C: n = 40 and Re(z) = -10
Option D: n = 20 and Re(z) = 10
Show/Hide Answer Key
Option C: n = 40 and Re(z) = -10
JEE Main Complex Numbers Questions No: 49
The equation |z – i| = |z – 1|, i = √-1, represents:
[2019]
Option A: a circle of radius 1/2
Option B: the line through the origin with slope 1
Option C: a circle of radius 1
Option D: the line through the origin with slope -1
Show/Hide Answer Key
Option B: the line through the origin with slope 1
JEE Mathematics Complex Numbers Questions No: 50
If Re[(z – 1) / (2z + i)] = 1, where z = x + iy, then the point (x, y) lies on a:
[2020]
Option A: circle whose center is at (-1/2, -3/2)
Option B: straight line whose slope is -2/3
Option C: straight line whose slope is 3/2
Option D: circle whose diameter is √5/2
Show/Hide Answer Key
Option D: circle whose diameter is √5/2
JEE Main Math Complex Numbers Questions No: 51
Let α = (-1 + i√3) / 2. If 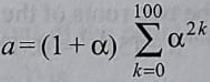
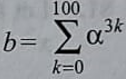
[2020]
Option A: x2 + 101x + 100 = 0
Option B: x2 – 102x + 101 = 0
Option C: x2 – 101x + 100 = 0
Option D: x2 + 102x + 101 = 0
Show/Hide Answer Key
Option B: x2 – 102x + 101 = 0
Complex Numbers JEE Questions No: 52
The imaginary part of (3 + 2√-54)1/2 – (3 – 2√-54)1/2 can be
[2020]
Option A: –√6
Option B: -2√6
Option C: 6
Option D: √6
Show/Hide Answer Key
Option B: -2√6
Complex Numbers JEE Main Questions No: 53
The value of 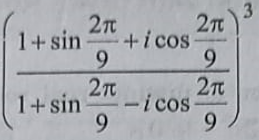
[2020]
Option A: (1/2)(1 – i√3)
Option B: (1/2)(√3 – i)
Option C: -(1/2)(√3 – i)
Option D: -(1/2)(1 – i√3)
Show/Hide Answer Key
Option C: –(1/2)(√3 – i)
Complex Numbers Questions for JEE Mains Questions No: 54
If a and b are real numbers such that (2 + α)4 = a + bα, where α = (-1 + i√3) / 2, then a + b is
[2020]
Option A: 9
Option B: 24
Option C: 33
Option D: 57
Show/Hide Answer Key
Option A: 9
Complex Numbers Questions and Answers No: 55
Let z = x + iy be a non-zero complex number such that z2 = i|z|2, where i = √-1, then z lies on the
[2020]
Option A: line y = -x
Option B: imaginary axis
Option C: line, y = x
Option D: real axis
Show/Hide Answer Key
Option C: line y = x
Complex Numbers Questions with Solutions No: 56
If (3 + isinθ) / (4 – icosθ), θ ∈ [0, 2π] is a real number, then an argument of sinθ + icosθ is
[2020]
Option A: π – tan-1(4/3)
Option B: π – tan-1(3/4)
Option C: -tan-1(3/4)
Option D: tan-1(4/3)
Show/Hide Answer Key
Option B: π – tan-1(3/4)
JEE Mains Complex Numbers Questions No: 57
If z be a complex number satisfying |Re(z)| + |Im(z)| = 4, then |z| cannot be equal to
[2020]
Option A: √17/2
Option B: √10
Option C: √7
Option D: √8
Show/Hide Answer Key
Option C: √7
JEE Mains Math Complex Numbers Questions No: 58
Let z be a complex number such that |(z – i) / (z + 2i)| = 1 and |z| = 5/2. Then, the value of |z + 3i| is
[2020]
Option A: √10
Option B: 7/2
Option C: 15/4
Option D: 2√3
Show/Hide Answer Key
Option B: 7/2
Complex Numbers Questions for JEE Questions No: 59
If z1, z2 are complex numbers such that Re(z1) = |z1 – 1|, Re(z2) = |z2 – 1| and arg(z1 – z2) = π / 6, then Im(z1 + z2) is equal to
[2020]
Option A: 2/√3
Option B: 2√3
Option C: √3/2
Option D: 1/√3
Show/Hide Answer Key
Option B: 2√3
Complex Numbers Problems for Class 11 Questions No: 60
The value of ((-1 + i√3) / (1 – i))30 is
[2020]
Option A: -215
Option B: 215i
Option C: -215i
Option D: 65
Show/Hide Answer Key
Option C: -215i
| JEE Main Mathematics Previous Year Questions with Solutions: Algebra |
| JEE Main Previous Year Mathematics Questions Set, Relations & Functions | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Complex Numbers | 1 to 30 | 31 to 60 | 61 to 81 | |
| JEE Main Previous Year Mathematics Questions Sequence & Series | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Quadratic Equations | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Permutations & Combinations | 1 to 30 | 31 to 60 | 61 to 94 | |
| JEE Main Previous Year Mathematics Questions Binomial Theorems | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Determinants & Matrices | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Mathematics Previous Year Questions with Solutions: Trigonometry |
| JEE Main Previous Year Mathematics Questions Trigonometry Ratios Identities | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Properties of Triangles | 1 to 31 | |
| JEE Main Previous Year Mathematics Questions Trigonometrical Equations | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Inverse Trigonometrical Functions | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Height & Distance | 1 to 27 | |
| JEE Main Mathematics Previous Year Questions with Solutions: Coordinate Geometry |
| JEE Main Previous Year Mathematics Questions Cartesian System & Straight Lines | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Circles | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Parabola | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Ellipse | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Hyperbola | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Mathematics Previous Year Questions with Solutions: Differential Equations |
| JEE Main Previous Year Mathematics Questions Limit, Continuity & Differentiability | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Differentiations | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Application of Derivative | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Mathematics Previous Year Questions with Solutions: Integral Calculus |
| JEE Main Previous Year Mathematics Questions Indefinite Integrals | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Definite Integrals | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Area By Integration | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Mathematics Previous Year Questions with Solutions: Differential Equations |
| JEE Main Previous Year Mathematics Questions Differential Equations | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Mathematics Previous Year Questions with Solutions: Vector & 3D Geometry |
| JEE Main Previous Year Mathematics Questions Vectors | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 139 | |
| JEE Main Previous Year Mathematics Questions 3D Geometry | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Mathematics Previous Year Questions with Solutions: Statistics & Probability |
| JEE Main Previous Year Mathematics Questions Statistics | 1 to 30 | 31 to 60 | 61 to 86 | |
| JEE Main Previous Year Mathematics Questions Probability | 1 to 30 | 31 to 60 | 61 to 95 | |
| JEE Main Mathematics Previous Year Questions with Solutions: Miscellaneous |
| JEE Main Previous Year Mathematics Questions Mathematical Induction | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |
| JEE Main Previous Year Mathematics Questions Mathematical Reasoning | 1 to 30 | 31 to 60 | 61 to 90 | 91 to 120 | 121 to 150 | |

