Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Prep Test 11 Grid Ins Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Math Prep Test 11 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
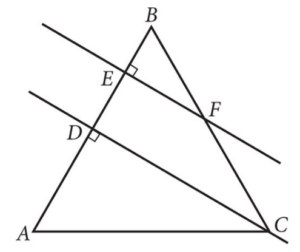
Triangle ABC shown above is an equilateral triangle cut by two parallel lines. If the ratio of BF to FC is 3:4 and EB = 3, what is the length of DE?
Show/Hide Answer Key
Correct Answer: 4
Difficulty: Medium
Category: Additional Topics in Math / Geometry
Strategic Advice: Start by marking up the figure with the information you’re given. You know the length of EB, which is 3. You also know the triangle is equilateral, which means all three sides are congruent and all three angles are 60°. This means angles A and B are both 60°, which further means that triangles BEF and ADC are 30-60-90 triangles, and therefore similar by the AAA theorem.
Getting to the Answer: Remember, 30-60-90 triangles have side lengths in the ratio x: x√3:2x, which means if EB is 3, then BF (the hypotenuse) is 2(3) = 6. Now, because you know the ratio of BF to FC, you can find the length of FC:
3/4 = 6/FC
3(FC) = 24
FC = 8
Now you can find the length of each side of the original equilateral triangle: 6 + 8 = 14, which is the length of AC, the hypotenuse of triangle ADC. This means side AD, being the shorter leg of triangle ADC, is 14 ÷ 2 = 7. You now have enough information to find the length of DE, which is AB – (AD + EB) = 14 – (7 + 3) = 4.
SAT Math Practice Online Test Question No 2:
If n5/2 = 32, what is the value of n?
Show/Hide Answer Key
Correct Answer: 4
Difficulty: Medium
Category: Passport to Advanced Math / Exponents
Strategic Advice: When solving any type of equation, you should always think of inverse operations. The inverse of raising a quantity to the 5/2 power is raising it to the 2/5 power.
Getting to the Answer: Eliminate the exponent using inverse operations and then go from there.
n2/5 = 32
n = 322/5
Now, you have two choices—you can enter this value into your calculator as 32^(2/5) or you can evaluate the number using the rules of exponents:
SAT Math Practice Online Test Question No 3:
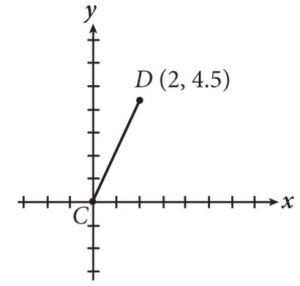
In the figure shown, line B (not shown) is parallel to CD and passes through the point (0, –1). If line B also passes through the point (2, y), what is the value of y?
Show/Hide Answer Key
Correct Answer: 3.5 or 7/2
Difficulty: Hard
Category: Heart of Algebra / Linear Equations
Strategic Advice: Remember that parallel lines have the same slope. Use the slope formula m = y2 – y1/x2 – x1 to find the slope of CD(bar).
Getting to the Answer: CD(bar) passes through the points (0, 0) and (2, 4.5), so its slope is 4.5 – 0/2 – 0 = 2.25. Line B has the same slope and passes through (0, –1), so you can use the slope formula again to find the y-coordinate of the given point, (2, y).
2.25 = y -(-1)/2 – 0
2.25 = y + 1/2
4.5 = y + 1
3.5 = y
The y-coordinate of the point is 3.5.
SAT Math Practice Online Test Question No 4:
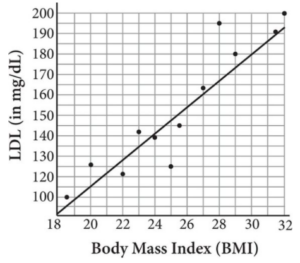
Body mass index, or BMI, is one of several measures used by doctors to determine a person’s health as indicated by weight and height. Low-density lipoprotein, or LDL cholesterol, known as the “bad” cholesterol, is another health indicator and consists of fat proteins that clog arteries. Following are the results of a study showing the relationship between BMI and LDL for 12 individuals and the line of best fit for the data.
A doctor’s patient has a BMI of 25 and an LDL level of 160. The doctor wants to calculate the percent error of this patient’s data compared to that predicted by the line of best fit. Suppose the doctor uses the points (20, 110) and (30, 180), which lie on the line of best fit, to model the equation. Based on this model, what is the percent error? Round to the nearest tenth of a percent and ignore the percent sign when entering your answer.
Show/Hide Answer Key
Correct Answer: 9.4
Difficulty: Hard
Category: Problem Solving and Data Analysis / Scatterplots
Strategic Advice: Percent error shows the deviation of an actual value from an expected value. The formula for percent error is [Expected value – Actual value]/Actual value. To find the expected value, you’ll need to find the equation of the line of best fit using the data points given in the question.
Getting to the Answer: First, determine the equation of the line of best fit. The slope is m = 180 – 110/30 – 20
m = 70/10
m = 7
So far, the equation looks like y = 7x + b. Next, use either of the two points to find b:
y = 7x + b
110 = 7(20) + b
110 = 140 + b
-30 = b
The equation is y = 7x – 30, so the expected value for a person with a BMI of 25 is 7(25) – 30 = 145. The doctor’s patient had an LDL of 160, so the percent error is [145 – 160]/160 = 15/160 = 0.09375
Be sure to follow directions. Rounded to the nearest tenth of a percent, the correct answer is 9.4.
SAT Math Practice Online Test Question No 5:
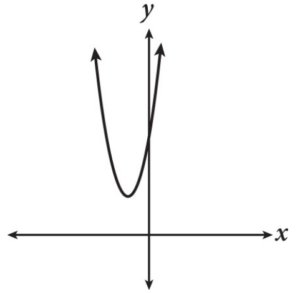
If the equation of the graph shown above is y = 2(x + 3)2 + 10, what is the y-intercept of the graph?
Show/Hide Answer Key
Correct Answer: 28
Difficulty: Medium
Category: Passport to Advanced Math / Quadratics
Strategic Advice: Graphically, a y-intercept is in the form (0, y), so the y-intercept of the graph is the value of y when 0 is substituted for x in the equation.
Getting to the Answer: Don’t forget to follow the correct order of operations as you simplify the expression.
y = 2(0 + 3)2 + 10
= 2(3)2 + 10
= 2(9) + 10 = 18 + 10 = 28
SAT Math Practice Online Test Question No 6:
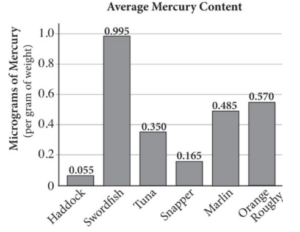
Mercury is a naturally occurring metal that can be harmful to humans. The current recommendation is for humans to take in no more than 0.1 microgram for every kilogram of their weight per day. Fish generally carry high levels of mercury, although certain fish have higher mercury content than others. Fish, however, are healthy sources of many other nutrients, so nutritionists recommend keeping them in the human diet. The figure below shows the average mercury content of several types of fish.
If a person weighs 82 kilograms, how many grams of snapper can he safely consume per day? Round your answer to the nearest gram.
Show/Hide Answer Key
Correct Answer: 50
Difficulty: Medium
Category: Problem Solving and Data Analysis / Statistics and Probability
Strategic Advice: The key to answering a question like this is in reading the labels on the graph carefully. You do not need to convert grams to micrograms or vice versa. They are simply the units for mercury content.
Getting to the Answer: Start by determining how many micrograms of mercury a person who weighs 82 kilograms can consume: 82 × 0.1 = 8.2 micrograms. Next, find snapper on the bar graph and determine how many micrograms it contains (per gram of weight): 0.165. Divide the number of micrograms the person can consume, 8.2, by the number in each gram of snapper to arrive at 8.2 ÷ 0.165 = 49.697, or about 50 grams.
SAT Math Practice Online Test Question No 7:
If g(x) = x2 + 2x + 9, what is g(5) – g(–1)?
Show/Hide Answer Key
Correct Answer: 36
Difficulty: Easy
Category: Passport to Advanced Math / Functions
Strategic Advice: When evaluating a function, substitute the value inside the parentheses for x in the equation.
Getting to the Answer: Evaluate the function at x = 5 and at x = –1. Then subtract the second output from the first. Note that this is not the same as first subtracting 5 – (–1) and then evaluating the function at x = 6.
f(5) = (5)2 + 2(5) + 9 = 25 + 10 + 9 = 44
f(-1) = (-1)2 + 2(-1) + 9 = 1 – 2 + 9 = 8
f(-5) – f(-1) = 44 – 8 = 36
SAT Math Practice Online Test Question No 8:
Sometimes, companies will buy stock in businesses owned by one or more of their competitors in order to gain some control over the competing companies. Suppose Company X buys stock in two of its competitors. The first competitor is a small regional company. Five hundred shares of its stock cost $25,000 less than half as much as 500 shares of the other competitor, which is a large national company. Together, Company X pays $155,000 for all the stock. How many more thousands of dollars did Company X spend on acquiring the stock of the national competitor than the regional one? Enter your answer in thousands of dollars. (For example, enter $15,000 as 15.)
Show/Hide Answer Key
Correct Answer: 85
Difficulty: Medium
Category: Heart of Algebra / Systems of Linear Equations
Strategic Advice: Write a system of equations with r = the cost of the regional competitor’s stock in thousands of dollars (so you don’t have to deal with all the zeros) and n = the cost of the national competitor’s stock in thousands of dollars. Before entering your final answer, check that you answered the right question (how much more the national competitor’s stock cost).
Getting to the Answer: Translate English into math to write the two equations: The regional competitor’s stock cost 25 thousand dollars less than half as much as the national competitor’s stock, so r = (1/2)n – 25. Together, both stock acquisitions cost 155 thousand dollars, so r + n = 155.
The system of equations is: {r + n = 155, r = n/2 – 25}
The bottom equation is already solved for r, so substitute r = (n/2) – 25 into the top equation for r and solve for n. To make the numbers easier to work with, multiply each term by 2 to clear the fractions:
(n/2) – 25 + n = 155
n – 50 + 2n = 310
3n = 360
n = 120
The national competitor’s stock cost 120 thousand dollars, so the regional competitor’s cost (120 ÷ 2) – 25 = 60 – 25 = 35 thousand dollars. This means the national competitor’s stock cost 120 – 35 = 85 thousand dollars more than the regional competitor’s stock.
SAT Math Practice Online Test Question No 9:
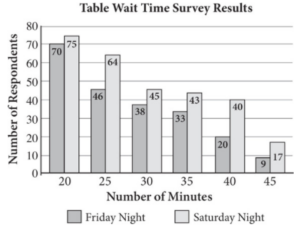
A restaurant sent out surveys to determine how long customers are willing to wait for a table on Friday night versus Saturday night. Participants randomly received either a Friday night or a Saturday night survey. Results are shown in the bar graph below.
On average, how many minutes longer are customers willing to wait for a table on Saturday night than on Friday night? Round your answer to the nearest whole minute.
Show/Hide Answer Key
Correct Answer: 1
Difficulty: Hard
Category: Problem Solving and Data Analysis / Statistics and Probability
Strategic Advice: Think about what the bar graph shows: times customers are willing to wait on Friday and Saturday. The question asks on average how much longer customers are willing to wait. So, you will need to find a weighted average for each day.
Getting to the Answer: Start with Friday. Multiply each wait time by the height of the bar (the number of people willing to wait for that amount of time on that night):
20 x 70 = 1,400
25 x 46 = 1,150
30 x 38 = 1,140
35 x 33 = 1,155
40 x 20 = 800
45 x 9 = 405
Next, add the results to get 6,050, and then divide by the total number of people who took the Friday survey (70 + 46 + 38 + 33 + 20 + 9 = 216): 6,050 ÷ 216 = 28.0 minutes. This is the average amount of time people are willing to wait for a table on Friday night. Now, do the same thing for Saturday.
20 x 75 = 1,500
25 x 64 = 1,600
30 x 45 = 1,350
35 x 43 = 1,505
40 x 40 = 1,600
45 x 17 = 765
Add the results, 8,320, and divide by the number of people (75 + 64 + 45 + 43 + 40 + 17 = 284) to get 8,320 ÷ 284 = 29.3 minutes. So, people are willing to wait 29.3 – 28.0 = 1.3 minutes longer on Saturday than Friday. Don’t forget to follow directions—1.3 rounded to the nearest whole minute is 1 minute.
SAT Math Practice Online Test Question No 10:
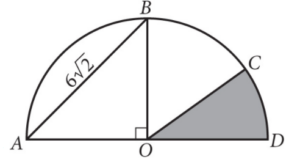
If AD is a diameter of the circle shown above, and the arc length of CD is π, what is the area of the shaded region? Use 3.14 to approximate π and round your answer to the nearest tenth.
Show/Hide Answer Key
Correct Answer: 9.4
Difficulty: Hard
Category: Additional Topics in Math / Geometry
Strategic Advice: This question requires logical thinking, knowledge of special right triangles, and knowing how to find arc length. It’s a challenging question, so if you’re pushed for time, skip it and come back later.
Getting to the Answer: Finding the area of a sector of a circle (the shaded region) requires knowing the degree measure of the corresponding interior angle. Given that information, your first step is to find the area of the entire circle. Then you’ll find the proportional amount represented by the sector. To find the area of a circle, the only thing you need is the radius. The radius is not shown in the figure, so you will have to think about special right triangles. In the figure, triangle ABO is formed by 2 radii and a 90° angle. This means the triangle must be a 45-45-90 triangle, and therefore its side lengths are in the ratio 1 : 1 :√2. The hypotenuse is given as 6√2 so the side lengths of the triangle, and therefore the radius of the circle, must be 6, and the area of the entire circle is A = πr2 = π(6)2 = 36π. Now you need to find the portion of the circle represented by the shaded region by finding the measure of the angle inside the sector and dividing by 360. You’ll need to use the given arc length, π, and the formula for finding arc length (arc length = θr, where θ is the interior angle and r is the length of the radius):
π = θ(6)
π/6 = θ
If you know your unit circle, you know this corresponds to 30°. If you don’t recall this fact, then you can convert radians to degrees by multiplying the radian measure by 180/π to get π/6 x 180/π = 180/6 = 30.
This means the shaded region makes up 30/360 = 1/12 of the total area of the circle, so divide the total area by 12 to get 36π ÷ 12 = 3π. The question tells you to approximate π using 3.14 and to round to the nearest tenth, so the final answer is 9.4.