Welcome to AMBiPi (Amans Maths Blogs). SAT (Scholastic Assessment Test) is a standard test, used for taking admission to undergraduate programs of universities or colleges in the United States. In this article, you will get SAT 2022 Math Practice Questions Test 12 Grid Ins Questions with Answer Keys | SAT Online Tutor AMBiPi.
SAT 2022 Math Practice Questions Test 12 Grid Ins Questions with Answer Keys
SAT Math Practice Online Test Question No 1:
Let 3x3/2(16x2)3/8x-1/2
What is the exponent on x when the expression above is written in the simplest form?
Show/Hide Answer Key
Correct Answer: 8
Difficulty: Hard
Category: Passport to Advanced Math / Exponents
Strategic Advice: Read the question carefully to determine what part of the expression you need to simplify and what part you don’t. Sometimes, you can work on a simpler question and still arrive at the correct answer.
Getting to the Answer: The question only asks for the exponent on x, so you do not have to simplify the coefficients. Rewrite the expression without the coefficients and simplify using the rules of exponents.
3x3/2 (16x2)3 /8x-1/2 = x3/2 (x2)3 /x-1/2
= x3/2 -(-1/2) . x2×3
= x3/2+1/2 . x6
= x2 . x6
= x8
The exponent on x is 8.
SAT Math Practice Online Test Question No 2:
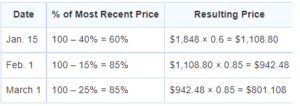
When a thrift store gets used furniture in good condition to sell, it researches the original price and then marks the used piece down by 40% of that price. On the first day of each of the following months, the price is marked down an additional 15% until it is sold or it reaches 30% of its original price. Suppose the store gets a piece of used furniture on January 15th. If the piece of furniture costs $1,848 new, and it is sold on March 10th of the same year, what is the final selling price, not including tax? Round your answer to the nearest whole dollar.
Show/Hide Answer Key
Correct Answer: 801
Difficulty: Hard
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: Draw a chart or diagram detailing the various price reductions for each 30-day period.
Getting to the Answer: You’ll need to make several calculations, so don’t round until the final answer.
You can stop here because the item was sold on March 10th. Before gridding in your answer, check that $801 is not less than 30% of the original price: 0.30 × $1,848 = $554.40. It’s not, so the final selling price, rounded to the nearest whole dollar, was $801.
SAT Math Practice Online Test Question No 3:
Recycling certain metals have been a common practice dating back to preindustrial times. For example, there is evidence of scrap bronze and silver being collected and melted down for reuse in a number of European countries. Today, there are recycling companies and even curbside collection bins for recycling. As a general rule, recycling companies pay for metals by weight. Suppose a person brings in 3 pounds of copper and receives $8.64, and 24 ounces of nickel and receives $10.08. If another person brings in equal weights of copper and nickel, what fractional portion of the money would he receive from the copper?
Show/Hide Answer Key
Correct Answer: 3/10
Difficulty: Hard
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: Whenever rates are given in different units, start by converting to the same units. In most cases, converting to the smaller unit avoids fractions and decimals.
Getting to the Answer: Start with nickel because the weight is already in ounces: $10.08 ÷ 24 = $0.42 per ounce. Now find the per-ounce rate for copper. There are 16 ounces in one pound, so three pounds is 48 ounces: $8.64 ÷ 48 = $0.18 per ounce. So, if a person were to bring in equal amounts of each, he would receive $0.18 per ounce of copper and $0.42 per ounce of nickel. To find the fractional portion he would receive from the copper, set up a comparison between the amount received for copper and the total amount received, $0.18 + $0.42 = $0.60. The portion of the total amount he receives from copper would be 0.18/0.60, which reduces to 3/10.
SAT Math Practice Online Test Question No 4:
The Bar Exam is a test given in each state to determine whether or not a law school graduate is competent to practice law. The American Bar Association surveyed 3,000 law school graduates across the country who passed the bar exam in 2000. Of those surveyed, 720 were not practicing law in 2012. If 55,200 graduates passed the bar in 2000, how many of them were practicing law in 2012, assuming the sample was a good representation of the population of law school graduates who passed the bar in 2000? Round to the nearest thousand and enter your answer in terms of thousands. (For example, enter 18,000 as 18.)
Show/Hide Answer Key
Correct Answer: 42
Difficulty: Easy
Category: Problem Solving and Data Analysis / Statistics and Probability
Strategic Advice: When a sample is a good representation of a population, you can apply the results of a study to the entire population.
Getting to the Answer: Start by finding the percent of the graduates who were surveyed that were not practicing law: 720 out of 3,000 = 720 ÷ 3,000 = 0.24, or 24%. The question asks about the number of graduates who were practicing law in 2012, so subtract from 100% to find that 76% of the graduates were practicing law in 2012. Apply this percentage to the whole population of graduates from 2000 who passed the bar: 55,200 × 0.76 = 41,952. Now, follow directions carefully—round to the nearest thousand (42,000) and enter your answer as the number of thousands, which is 42.
SAT Math Practice Online Test Question No 5:
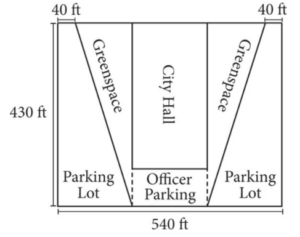
Many cities try to work “greenspaces” into their city planning because living plants help filter the city’s air, reducing the effects of pollution. The figure above shows the plans for a new green space around City Hall, which will be created by converting portions of the existing parking lots. If the width of each parking lot is the same as the width of the City Hall building, how many thousands of square feet of green space will there be after the conversion? Round to the nearest thousand and enter your answer in terms of thousands. (For example, enter 14,000 as 14.)
Show/Hide Answer Key
Correct Answer: 60
Difficulty: Medium
Category: Additional Topics in Math / Geometry
Strategic Advice: Whenever a question asks about the amount of space something covers (here, the greenspace), you are looking for an area. In this question, the area that you’re looking for takes on the shape of a right triangle (actually, two of them), so use the formula A = (1/2)bh.
Getting to the Answer: The key to answering this question is in labeling the diagram. The calculations are very straightforward once you have the correct dimensions of the triangles. You’re given that the width of each parking lot is equal to the width of the City Hall building, so each parking lot is 540 ÷ 3 = 180 feet wide. This means the base of each triangle (at the top of the diagram) is 180 – 40 = 140 feet. The height of each triangle is the same as the length of the parking lot, which is 430 feet.
You now have all the numbers you need. The area of each triangle is 1/2(140)(430) = 30,100, so both triangles together result in a green space that covers 60,200 square feet. Rounded to the nearest thousand, this is 60,000, which should be gridded in as 60.
SAT Math Practice Online Test Question No 6:
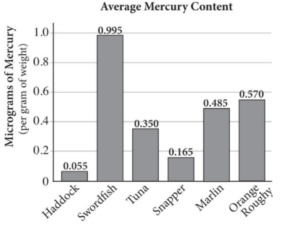
Mercury is a naturally occurring metal that can be harmful to humans. The current recommendation is for humans to take in no more than 0.1 micrograms for every kilogram of their weight per day. Fish generally carry high levels of mercury, although certain fish have higher mercury content than others. Fish, however, are healthy sources of many other nutrients, so nutritionists recommend keeping them in the human diet. The figure below shows the average mercury content of several types of fish.
Suppose in a week, a person regularly eats one portion of each type of fish shown in the bar graph, except the fish with the highest mercury content. What is this person’s average daily mercury consumption, in micrograms, assuming a portion size of 100 grams? Round your answer to the nearest microgram.
Show/Hide Answer Key
Correct Answer: 23
Difficulty: Hard
Category: Problem Solving and Data Analysis / Statistics and Probability
Strategic Advice: There is a lot of information to sort through in a question like this. Make a plan and carry out the plan one step at a time. Don’t try to keep all the calculations in your calculator; jot them down as you work through each step. Getting to the Answer: Multiply the average portion size (100 grams) by each mercury content shown in the bar graph. Don’t forget to remove the swordfish, because it has the highest mercury content. Then, find the average—but be careful, you’re finding an average over 7 days (the number of days in a week), not 5 (the number of portions the person consumes).
Haddock: 0.055 × 100 = 5.5
Tuna: 0.350 × 100 = 35
Snapper: 0.165 × 100 = 16.5
Marlin: 0.485 × 100 = 48.5
Orange Roughy: 0.570 × 10 = 57
The total is 162.5 micrograms, which means the average daily consumption over the whole week is 162.5 ÷ 7 = 23.214, or about 23 micrograms. (Note that unless this person weighs 230 kg, which is a little over 500 pounds, then they are consuming way too much mercury per day.)
SAT Math Practice Online Test Question No 7:
A North Carolina agricultural supply company is hoping to expand its services to three counties in rural Virginia. According to its research, there is a total of approximately 1,200 farms in these three counties. The company sends out surveys to a sample of 200 randomly selected farmers in the counties and finds that 120 are not satisfied with their current supply company. Based on other market research, the company is confident that it will be able to acquire 75% of the dissatisfied customers. Based on this information and the results of the sample survey, how many customers should the company be able to acquire in these three counties?
Show/Hide Answer Key
Correct Answer: 540
Difficulty: Medium
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: Work through this question one step at a time. Start by using the sample survey to find the percentage of farmers who are not satisfied with their current supply company.
Getting to the Answer: According to the sample survey, 120/200 = 0.6 (or 60%), of the farmers are not satisfied with their current supply company. Multiply the total number of farms in the population (the three counties) to find that 1,200 × 0.6 = 720 farmers are not satisfied. The company is confident that it can acquire 75% of these customers, or 720 × 0.75 = 540 customers.
SAT Math Practice Online Test Question No 8:
The Mackinac Bridge in Michigan is one of the longest suspension bridges in the Western Hemisphere, spanning approximately 1.63 miles from one end to the other. It has several pieces that are connected by anchorages (large blocks to which the suspension cables are attached). The longest piece is 3,800 feet long. In a scale drawing on a poster board, the length of the bridge is 28 inches. How many inches long should the longest piece be? Round your answer to the nearest tenth of an inch. (There are 5,280 feet in 1 mile.)
Show/Hide Answer Key
Correct Answer: 12.4
Difficulty: Hard
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: Pay careful attention to the units. You need to convert the length of the whole bridge to feet and then set up and solve a proportion.
Getting to the Answer: You don’t need to convert all of the dimensions to inches, even though the answer asks for inches. The ratio will be the same. But you do need to convert the length of the bridge, given in miles, to feet, because the length of the longest piece of the bridge is given in feet: 1.63 miles × 5,280 feet = 8,606.4 feet. Now, set up a proportion and solve for the unknown. Use words first to help you keep the dimensions in the right places:
actual longest price/actual total length = drawing longest price/drawing total length
3,800/8,606.4 = x/28
106,400 = 8,606.4x
12.36 ≈ x
The length of the longest piece in the drawing should be 12.4 inches long.
SAT Math Practice Online Test Question No 9:
If –10 < 14 – 2p < 6, what is the greatest possible integer value of 7 – p?
Show/Hide Answer Key
Correct Answer: 2
Difficulty: Easy
Category: Heart of Algebra / Inequalities
Strategic Advice: When a question asks for the value of an expression, rather than the value of the variable alone, try to determine how the desired expression is related to what is given in the question.
Getting to the Answer: Notice that 7 – p is half of 14 – 2p. This means you can cut all parts of the inequality in half to arrive at the correct answer.
-10/2 < (14 – 2p)/2 < 6/2
-5 < 7 – p < 3
There is no need to solve for p because the question asks about 7 – p. The inequality (<) doesn’t include 3, so the greatest possible integer value of 7 – p is 2.
SAT Math Practice Online Test Question No 10:
Selena is taking a 90-minute test that consists of 50 multiple-choice questions and 30 true-false questions. If she completes 48 questions in 50 minutes, how many seconds per question does she have on average to answer each of the remaining questions?
Show/Hide Answer Key
Correct Answer: 75
Difficulty: Medium
Category: Problem Solving and Data Analysis / Rates, Ratios, Proportions, and Percentages
Strategic Advice: Pay careful attention to the units in a question like this. Here, the rate is given in minutes, but the question asks for the answer in seconds.
Getting to the Answer: The test consists of a total of 50 + 30 = 80 questions. Selena has already answered 48 of the 80 questions. This means she has 80 – 48 = 32 questions left. She has used up 50 of the 90 minutes, leaving 40 minutes to complete the test. To find the amount of time per question she has left, divide the remaining time by the number of questions remaining: 40 minutes ÷ 32 questions = 1.25 minutes per question. Don’t forget to change your answer to seconds. There are 60 seconds in 1 minute, so multiply 1.25 × 60 to find that she has 75 seconds per question.