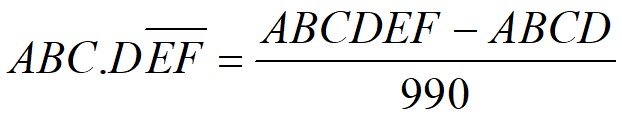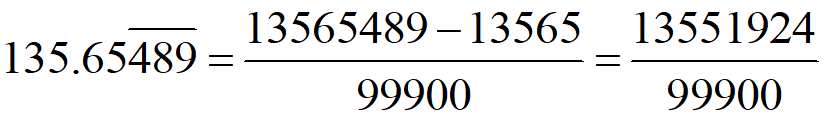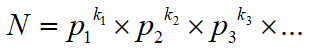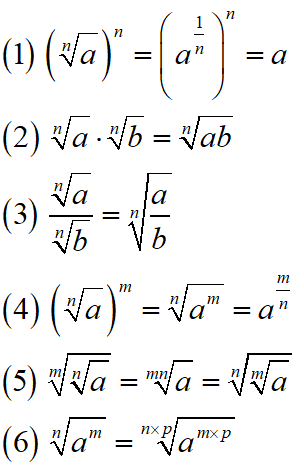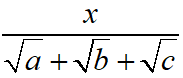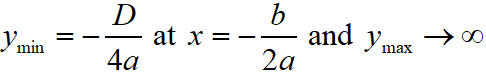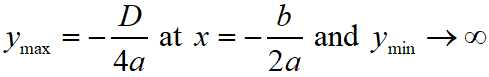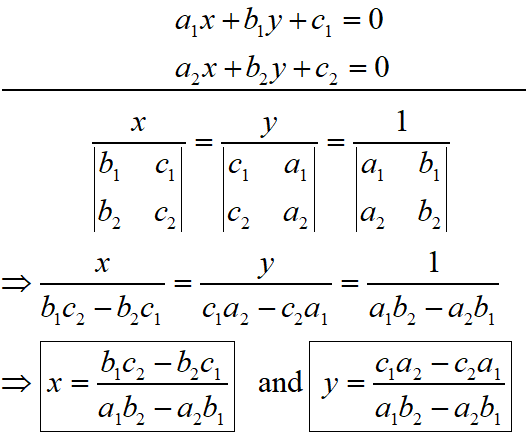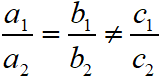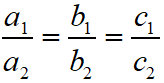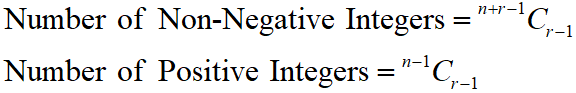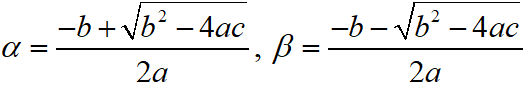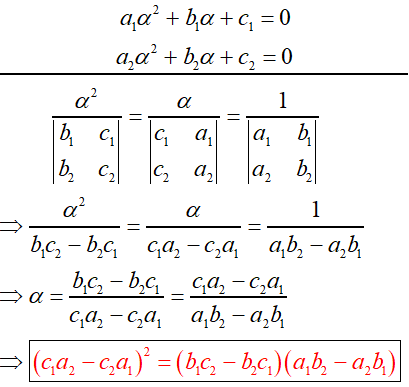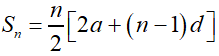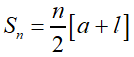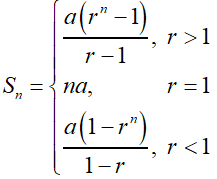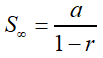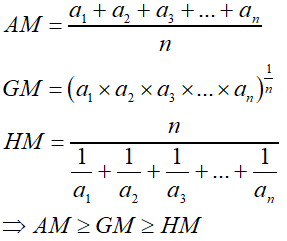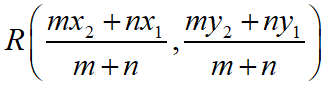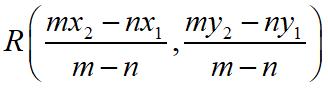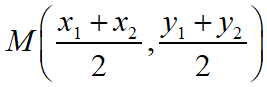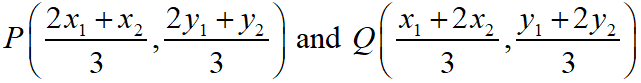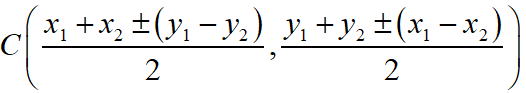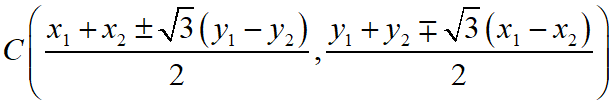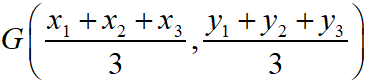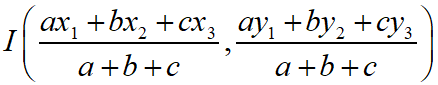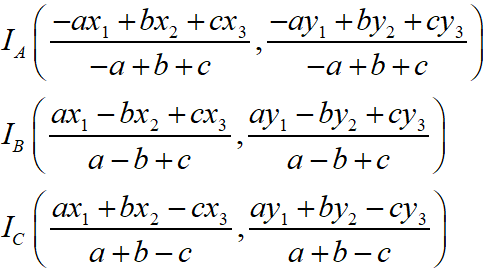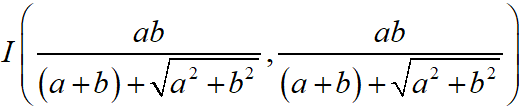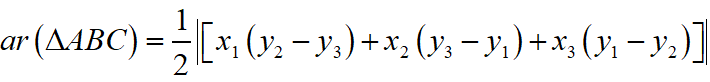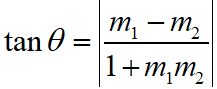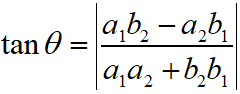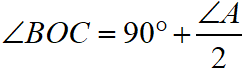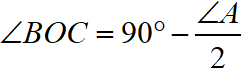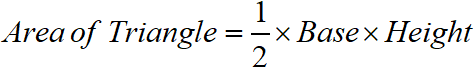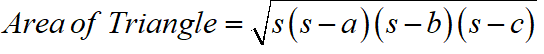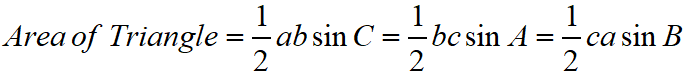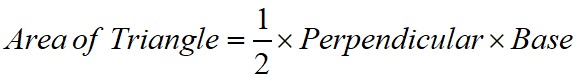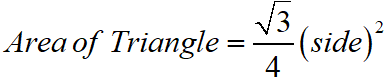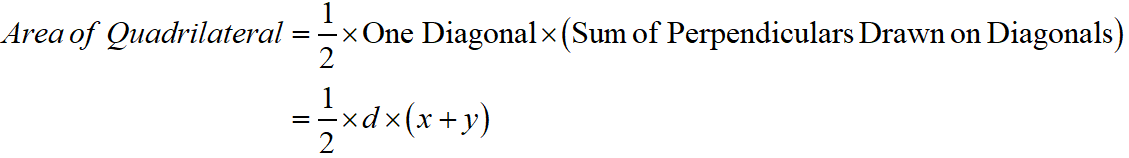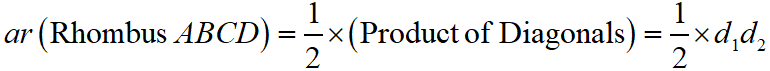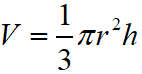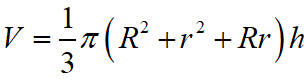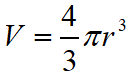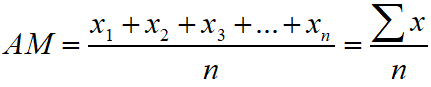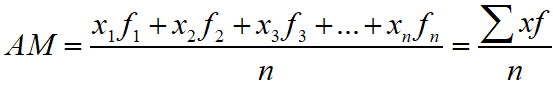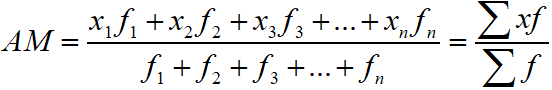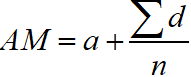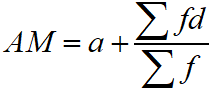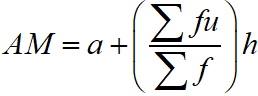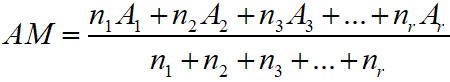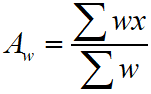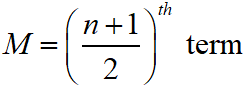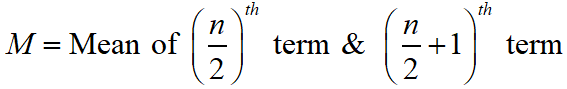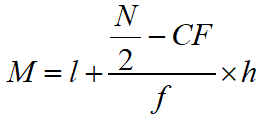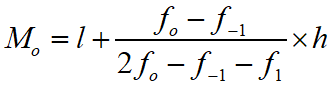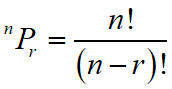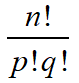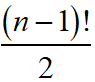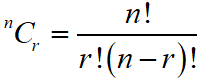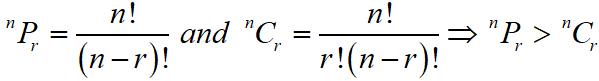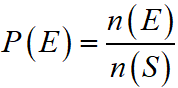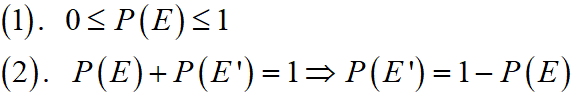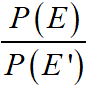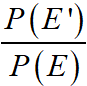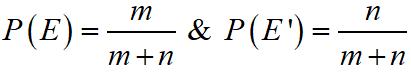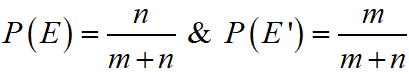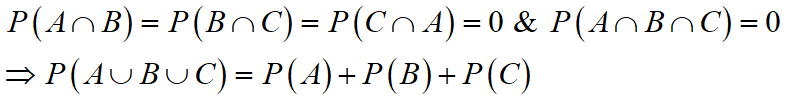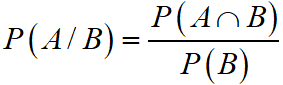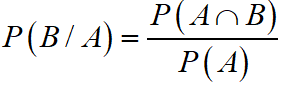Maths Short Tricks for NTSE NSEJS JSTSE Exams

Hi students, welcome to Amans Maths Blogs (AMB). In this post, you will get Maths Short Tricks for NTSE NSEJS JSTSE Exams. These maths shortcuts will help you to solve the mathematics questions asked in NTSE NSEJS or JSTSE exams. These competitive exams are very important for the CBSE Class 9 and 10. So the students learn these maths short tricks and practice on solving the previous year questions of NTSE exam or NSEJS exam or JSTSE exams etc. Some of the concepts are NOT covered in the syllabus of NSEJS and JSTSE. So kindly check your syllabus. Now, lets start.

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

NTSE Maths Combo Pack EBook

Get 900+ NTSE Maths Previous Year Question Bank with Solutions and 11 Mock Test Papers EBook for NTSE exams. For more details, Click To NTSE Stage 1 Mock Test SAT Maths and NTSE Stage 2 Mock Test SAT Maths. To get this combo ebook, click below RED button.

900+ Math Questions Bank & 11 Mock Test Paper for NTSE Stage 1 & 2 SAT (Maths)

NSEJS Maths Questions Bank EBook

Get NSEJS 2008 to 2018 Maths Questions Bank with Solutions. To get this combo ebook, click below RED button.

NSEJS Maths Questions Bank with Solutions

Maths Short Tricks in Number Systems

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 1 : Classification of Numbers

There are following classification of numbers:

Natural Numbers: All counting numbers are known as natural numbers. The collection of natural number is denoted by N. It means, N = {1, 2, 3, . . .}.

Whole Numbers: All natural numbers together with 0 are known as whole numbers. The collection of whole number is denoted by W. It means, W = {1, 2, 3, . . .}.

Integers: All natural numbers, 0 and negative of natural numbers are known as integers. The collection of integers is denoted by Z. It means, Z = {…, -3, -2, -1, 0, 1, 2, 3, …}. The natural numbers is also known as positive integers and the whole numbers are also known as non-negative integers.

Rational Numbers: A number that can be written in the form of p/q, where p and q are integers and q 0. The rational numbers can be terminating decimals (for example 1/5 = 0.2) or non-terminating and recurring decimals (for example: 1/3= 0.333…). The collection of rational numbers is denoted by Q. It means, Q = {2/3, -1/5, 12, -5…}.

Irrational numbers: The numbers which are not rational numbers means non-terminating and non-recurring decimals are known as irrational numbers. For example: √2, √15, (12)^(1/4), √(2+√2)  etc.

Real Numbers: The collection of rational and irrational numbers are known as real numbers. The real numbers can be represented on a number line. It is denoted by R. The square of a real numbers is always positive.

Imaginary Numbers: A number whose square is negative is known as imaginary numbers. For example, 3i, -2i etc where i = √(-1).

Fraction: A number that can be written in the form of p/q, where p and q are whole numbers and q 0. A rational number can be positive or negative. But, a fraction is positive only. For example: 2/3, 1/5, 12, 5… etc.

Prime Numbers: All natural numbers that is divisible by 1 and itself is known as prime numbers. Thus, the number of factors of a prime number is 2 only. The natural number 1 is NOT a prime number. For example: 2, 3, 5, 7, 11, 13, … etc.

Co-Prime Numbers: If the HCF of two numbers is 1, then both the numbers are co-prime to each other. Two consecutive numbers are always co-prime numbers. For example: 7 and 9 are co-prime to each other as HCF(7, 9) = 1.

Composite Numbers: All natural numbers, which is NOT prime are composite numbers. Thus, the number of factors of a composite number is more than 2. For example: 4, 6, 9, 16, 18 etc.

Read: Some More Concepts About Rational Numbers

Maths Short Trick 2 : Properties of Rational and Irrational Numbers

Some of the properties of rational and irrational numbers are as below:

Property 1: Sum of difference of a rational and an irrational number is irrational.

Property 2: The product and quotient of non-zero rational and irrational number is irrational.

Property 3: If we add, subtract, multiply or divide two irrational numbers, then the result may be rational or irrational numbers.

Property 4: Rational numbers satisfy the commutative, associative and distributive laws for addition and multiplication.

Property 5: Irrational numbers also satisfy the commutative, associative and distributive laws for addition and multiplication.

Maths Short Trick 3 : Recurring Decimal To Fraction

To express the recurring decimal number in a fraction, we use a formula as below.

where 999… as many times as the number recurring digits and 000… as many times as the number non-recurring digits after decimal point. In the following, the number of recurring digits (E and F) is 2, we write 9 as two times and the number of non-recurring digits (D) after decimal point is 1, we write 0 as one time. For example:

Read: How to Identify a fraction is Terminating or Non-Terminating Decimal

Maths Short Trick 4 : BODMAS Rule

The BODMAS is a concept that help us to simplify the math problems containing more than one mathematical operators. BODMAS is an acronym.

Thus, according to BODMAS rule,

First, we solve the brackets (B) and the order of brackets is as Small ( ), Curly or Middle { } and at last Square or Big [ ], if the math question contains.

And then, we solve the order (O). The order means exponent or index. Therefore, BODMAS rule is also known as BEDMAS (in this, E means Exponents) or BIDMAS (in this, I means Index). It means, we solve the exponent if the math problem contains.

And then, we solve the division (D), if the math question contains.

And then, we solve the multiplication (M), if the math question contains.

And then, we solve the addition (A), if the math question contains.

And then, we solve the subtraction (S), if the math question contains.

Read: More details about BODMAS

Vinculum Bar : When an algebraic expression contains Vinculum bar, then before applying BODMAS rule, we simplify the expression under the Vinculum bar.

Maths Short Trick 5 : Factors and Multiplies

Learn some basic definition about factors and multiples:

Factors: Factors of a number are the exact divisors of the number. It is a number that can be multiplied to get another number.

If ‘a‘ is a factor of ‘b‘, then a x n = b, where n is any natural number.

1 is a factor of all number as 1 x a = a.

Factor of a number cannot be greater than the number. The largest factor of a number is the number itself.

Factors of a number lie between 1 and the number itself (both inclusive). Thus, the number of factors of a number is finite.

For example: The factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.

Multiple: A multiple of a number is a number that is the product of a given number and some other natural number. 

If ‘a‘ is a multiple of ‘b‘, then b x n = a, where n is any natural number.

Multiple of a number is greater than or equal to the number. The smallest multiple of a number is the number itself.

Thus, the number of multiples of a number is infinite.

For example: The multiples of 7 are 7, 14, 21, 28, 35, 42 …etc.

Maths Short Trick 6 : Number of Factors

To find the number of factors of a number, first we do the prime factorization of the number.

Let a number N and its prime factorization is

Where p₁, p₂, p₃, … are prime factors and k₁, k₂, k₃, … are positive integers.

Then, the number of factors of N is (k₁ + 1)(k₂ + 1)(k₃ + 1)…

For example: 72 = 23 x 32. Then, the number of factors of 72 is (3 + 1)(2 + 1) = 4 x 3 = 12. As we have seen that the factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.

Maths Short Trick 7 : Some Results About HCF 

Result 1 : If we need to find the greatest number that will exactly divide p, q, r, then the required number = HCF (p, q, r).

For example: Greatest number that will exactly divide 65, 52 and 78 is HCF (65, 52, 78) = 13.

Result 2 : If we need to find the greatest number that will divide p, q and r leaving remainders a, b and c respectively, then the required number = HCF [(p – a), (q – b), (r – c)].

For example: Greatest number that will divide 65, 52 and 78 leaving the remainders 5, 2 and 8 is HCF [(65-5), (52-2), (78-8)] = HCF [60, 50, 70] = 10

Result 3 : If we need to find the greatest number that will divide p, q and r leaving the same remainders in each case, then the required number = HCF [(p – q), (q – r), (r – p)].

For example: Greatest number that will divide 65, 81 and 145 leaving the same remainders in each case is HCF [(81-65), (145-81), (145-65)] = HCF [16, 64, 80] = 16.

Maths Short Trick 8 : Some Results About LCM

Result 1 : If we need to find the least number which is exactly divisible by p, q and r, then the required number = LCM [p, q, r].

For example: Least number that will exactly divisible by 6, 5 and 7 is LCM (6, 5, 7) = 210.

Result 2 : If we need to find the least number which when divided by p, q and r leaves the remainders a, b and c respectively such that (p – a) = (q – b) = (r – c) = k, then the required number = LCM [p, q, r] – k.

For example: Least number which when divided by 6, 7 and 9 leaves the remainder 1, 2 and 4 respectively such that (6 – 1) = (7 – 2) = (9 – 4) = 5 is LCM [6, 7, 9] – 5 = 126 – 5 = 121.

Result 3 : If we need to find the least number which when divided by p, q and r leaves the same remainder ‘a‘ in each case, then the required number = LCM [p, q, r] + a.

For example: Least number that will exactly divisible by 6, 5 and 7 is LCM (6, 5, 7) = 210.

Maths Short Trick 9 : HCF and LCM

HCF of Fractions = (HCF of Numerators) / (LCM of denominators)

LCM of Fractions = (LCM of Numerators) / (HCF of denominators)

For any two numbers a and b, HCF(a, b) x LCM(a, b) = a x b

Maths Short Trick 10 : Divisibility Rules

Divisibility Rule of 2 = If the unit digit of a number is an even number or zero (0), then the number is divisible by 2.

Divisibility Rule of 3 = If the sum of the digits of a number is divisible by 3, then the number is divisible by 3.

Divisibility Rule of 4 = If the number formed by last two digits of a number is divisible by 4, then the given number is divisible by 4.

Divisibility Rule of 5 = If the unit digit of a number is 5 or zero (0), then the number is divisible by 5.

Divisibility Rule of 6 = If a number is divisible by 2 and 3 both, then the number is divisible by 6.

Divisibility Rule of 7 = First, double the last digit of given number and then subtract it from the remaining number. If the difference is 0 or divisible by 7, then the given number is divisible by 7.

Divisibility Rule of 8 = If the number formed by last three digits of a number is divisible by 8, then the given number is divisible by 8.

Divisibility Rule of 9 = If the sum of the digits of a number is divisible by 9, then the number is divisible by 9.

Divisibility Rule of 10 = If the last digit of a number is 0, then the number is divisible by 10.

Divisibility Rule of 11 = If the difference between sum of the digits at even places and sum of the digits at odd places of a number is zero (0) or divisible by 11, then the given number is divisible by 11.

Divisibility Rule of 12 = If a number is divisible by 3 and 4 both, then the number is divisible by 12.

Divisibility Rule of 13 = First, four times the last digit of given number and then add it to the remaining number. If the sum is divisible by 13, then the given number is divisible by 13.

Divisibility Rule of 14 = If a number is divisible by 2 and 7 both, then the number is divisible by 14.

Divisibility Rule of 15 = If a number is divisible by 3 and 5 both, then the number is divisible by 15.

Divisibility Rule of 16 = If the number formed by last four digits of a number is divisible by 16, then the given number is divisible by 16.

Divisibility Rule of 17 = First, five times the last digit of given number and then subtract it from the remaining number. If the difference is 0 or divisible by 17, then the given number is divisible by 17.

Divisibility Rule of 18 = If a number is divisible by 2 and 9 both, then the number is divisible by 18.

Divisibility Rule of 19 = First, double the last digit of given number and then add it to the remaining number. If the sum is divisible by 17, then the given number is divisible by 19.

Maths Short Trick 11 : Divisibility Results

Result 1 : (xⁿ – aⁿ) is divisible by (x – a) for all values of n.

Result 2 : (xⁿ – aⁿ) is divisible by (x + a) for all even values of n.

Result 3 : (xⁿ + aⁿ) is divisible by (x + a) for all odd values of n.

Maths Short Trick 12 : Euclid’s Division Lemma

Given two positive integers a and b, there exist unique integers q and r such that a = bq + r, 0 ≤ r < b.

It means, the remainder in any division is always positive.

This is same as division algorithm, Dividend = (Divisor x Quotient) + Remainder.

Euclid’s division lemma is used to find the highest common factor (HCF) of two positive integers.

Maths Short Trick 13 : Cyclicity (How to Find Last Digit of xⁿ)

Cyclicity is a concept that used to finding the last digit of xn. According to it,

Cyclicity of 0, 1, 5 and 6 is 1, it means: 0, 1, 5 and 6 repeat its unit digit after every consecutive power. Thus,

Last digit of  any number of the form (…0)^{Any Power} = 0

Last digit of  any number of the form (…1)^{Any Power} = 1

Last digit of  any number of the form (…5)^{Any Power} = 5

Last digit of  any number of the form (…6)^{Any Power} = 6

Cyclicity of 2, 3, 7 and 8 is 4, it means: 2, 3, 7 and 8 repeat its unit digit after every four power. Thus,

For any number ending with the digit 2,

Last digit of  any number of the form (…2)^{(Multiple of 4) + 1} = 2

Last digit of  any number of the form (…2)^{(Multiple of 4) + 2} = 4

Last digit of  any number of the form (…2)^{(Multiple of 4) + 3} = 8

Last digit of  any number of the form (…2)^{(Multiple of 4)} = 6

For any number ending with the digit 3,

Last digit of  any number of the form (…3)^{(Multiple of 4) + 1} = 3

Last digit of  any number of the form (…3)^{(Multiple of 4) + 2} = 9

Last digit of  any number of the form (…3)^{(Multiple of 4) + 3} = 7

Last digit of  any number of the form (…3)^{(Multiple of 4)} = 1

For any number ending with the digit 7,

Last digit of  any number of the form (…7)^{(Multiple of 4) + 1} = 7

Last digit of  any number of the form (…7)^{(Multiple of 4) + 2} = 9

Last digit of  any number of the form (…7)^{(Multiple of 4) + 3} = 3

Last digit of  any number of the form (…7)^{(Multiple of 4)} = 1

For any number ending with the digit 8,

Last digit of  any number of the form (…8)^{(Multiple of 4) + 1} = 8

Last digit of  any number of the form (…8)^{(Multiple of 4) + 2} = 4

Last digit of  any number of the form (…8)^{(Multiple of 4) + 3} = 2

Last digit of  any number of the form (…8)^{(Multiple of 4)} = 6

Cyclicity of 4 and 9 is 2, it means: 4 and 9 repeat its unit digit after every two power. Thus,

For any number ending with the digit 4,

Last digit of  any number of the form (…4)^{(Even Power)} = 6

Last digit of  any number of the form (…4)^{(Odd Power)} = 4

For any number ending with the digit 9,

Last digit of  any number of the form (…9)^{(Even Power)} = 9

Last digit of  any number of the form (…9)^{(Odd Power)} = 1

Get : Pre RMO & RMO Important PDFs

Maths Short Tricks in Surds

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 14 : What is Surds?

Let ‘a‘ be a rational number and ‘n‘ be a positive integer, then the irrational number is of the form

is known as surds where ‘a‘ is called radicand and the symbol of nth-root is known as radical sign. The ‘n‘ is called order of the surd.

Maths Short Trick 15 : Laws of Surds

There are following laws of surds:

Maths Short Trick 16 : Rationalization of Surds

If the product of two surds is a rational number, then each surd is known as rationalizing factor (RF) of other.

Monomial Surd: The general form of a monomial surd is ⁿ√a and its rationalizing factor (RF) is a^(1-1/n).

Binomial Surd: The general form of a binomial surd is (a + √b), (a – √b), (√a + √b), (√a – √b). 

The rationalizing factor of (√a + √b) is (√a – √b).

The rationalizing factor of (√a – √b) is (√a + √b).

Trinomial Surd: A surd which consisit of three terms, at least two which are monomial surds is called a trinomial surd. It means the general form of trinomial is (a + √b + √c) or (√a + √b + √c).

To rationalize a surds of the form

Step 1 : Multiply and divide by (√a + √b – √c) and then simplify it.

Step 2 : Finally multiply and divide by (a + b – c) – 2√(ab).

Maths Short Tricks in Exponent/Index

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 17 : What is Exponent?

The repeated multiplication of the same factor can be written in compact form as exponential form. It means, a x a x a x a x … to n times = aⁿ.

Maths Short Trick 18 : Laws of Exponents

Exponent Rule 1 : a⁰ = 1.

Exponent Rule 2 : a^m x aⁿ = a^m+n.

Exponent Rule 3 : a^m / aⁿ = a^m-n.

Exponent Rule 4 : a^m x b^m = (ab)^m.

Exponent Rule 5 : a^-n = 1 / aⁿ.

Exponent Rule 6 : (a^m)ⁿ = a^mn.

Maths Short Tricks in Logarithm

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 19 : What is logarithm?

If ‘a‘ is a positive real number, other than 1 and x is rational number such that a^x = n, then x is the logarithm of n to the base a. It means, if a^x = n, then x = log_an. where a > 0, a 1 and n > 0.

The base of a logarithm is always positive.

Read : Why the base of a logarithm cannot be negative?.

The base of a logarithm is cannot be unity.

Read : Why the base of a logarithm cannot be unity?.

Maths Short Trick 20 : Logarithmic Rules

There are following logarithmic rules for any base a (where a > 0 and a 1).

Logarithm Rule 1 : log_a1 = 0.

Logarithm Rule 2 : log_aa = 1.

Logarithm Rule 3 : log_a0 = Not Defined.

Read : Why the log of zero is NOT defined?.

Logarithm Rule 4 : log_a(-ve) = Not Defined.

Read : Why the log of any negative number is NOT defined?.

Logarithm Rule 5 : log_a(mn) = log_a(m) + log_a(n).

Logarithm Rule 6 : log_a(m/n) = log_a(m) – log_a(n).

Logarithm Rule 7 : log_a(m)ⁿ = nlog_a(m).

Logarithm Rule 8 : log_ab = log_c(b) / log_c(a).

Logarithm Rule 9 : log_a(b) x log_b(a) = 1.

Logarithm Rule 10 : a^(log_an) = n.

Logarithm Rule 11 : p^(log_aq) = q^(log_ap).

Logarithm Rule 12 : log_ax = log_ay , then x = y.

Maths Short Tricks in Polynomials

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 21 : What is Polynomial?

An algebraic expression p(x) of the form of p(x) = a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + … + a₂x² + a₁x + a₀, where a₀, a₁, a₂, …, a_n are real numbers and n is a non-negative integers.

The highest exponent n of the polynomial is the degree of the polynomial.

The degree of a constant polynomial p(x) = k is zero.

The degree of a zero polynomial p(x) = 0 is not defined.

The standard form of linear polynomial is p(x) = ax + b.

The standard form of quadratic polynomial is p(x) = ax² + bx + c.

The standard form of cubic polynomial is p(x) = ax³ + bx² + cx + d.

Maths Short Trick 22 : Remainder Theorem

Let ‘p(x)‘ be any polynomial of degree greater than or equal to one and a be any real number.

If a polynomial p(x) is divided by a linear polynomial (x – a), then the remainder is constant polynomial p(a) = r. It means, p(x) = (x – a)q(x) + r.

If a polynomial p(x) is divided by a quadratic polynomial (ax² + bx + c), then the remainder may be a linear polynomial (mx + n). It means, p(x) = (ax² + bx + c)q(x) + (mx + n).

If a polynomial p(x) is divided by a cubic polynomial (ax³ + bx² + cx + d), then the remainder may be a quadratic polynomial (mx² + nx + t). It means, p(x) = (ax³ + bx² + cx + d)q(x) + (mx² + nx + t).

Thus, the degree of the remainder always less than the degree of a divisor.

Maths Short Trick 23 : Factor Theorem

Let ‘p(x)‘ be any polynomial of degree greater than or equal to one and a be any real number such that p(a) = 0, then (x – a) is a factor of p(x).

Maths Short Trick 24 : HCF & LCM of Polynomials

Let ‘p(x)‘ and ‘q(x)‘ be any two polynomials. Then, HCF x LCM = p(x) x q(x).

If HCF and LCM and one of the polynomial p(x) are given, then other polynomial is q(x) = (HCF x LCM) / p(x).

If p(x) and q(x) and HCF are given, then other polynomial is LCM = [p(x) x q(x)] / HCF.

If p(x) and q(x) and LCM are given, then other polynomial is HCF = [p(x) x q(x)] / LCM.

Maths Short Trick 25 : Relation Between Roots & Coefficients of Polynomials

For quadratic polynomial p(x) = ax² + bx + c, sum of the roots is α + β = -b/a and product of the roots is αβ = c/a.

For cubic polynomial p(x) = ax³ + bx² + cx + d, sum of the roots is α + β + γ = -b/a and the sum of product of roots two at a time is αβ + βγ + γα = c/a and the product of the roots is αβγ = -d/a.

For biquadratic polynomial p(x) = ax⁴ + bx³ + cx² + dx + e, sum of the roots is α + β + γ + δ = -b/a and the sum of product of roots two at a time is αβ + αγ + αδ + βγ + βδ + γδ = c/a and the sum of the product of the roots three at a time is αβγ + αβδ + αγδ + βγδ = -d/a and the product of the roots is αβγδ = e/a.

Maths Short Trick 26 : Formation of Polynomials

If two roots α and β are given, then the quadratic polynomial p(x) = k(x – α)(x – β) = k[x² – (α + β)x + αβ]

If three roots α, β and γ are given, then the cubic polynomial p(x) = k(x – α)(x – β)(x – γ) = k[x³ – (α + β + γ)x² + (αβ + βγ + γα)x – αβγ]

If three roots α, β, γ and δ are given, then the biquadratic polynomial p(x) = k(x – α)(x – β)(x – γ)(x – δ) = k[x⁴ – (α + β + γ + δ)x³ + (αβ + αγ + αδ + βγ + βδ + γδ)x² – (αβγ + αβδ + αγδ + βγδ)x + αβγδ].

Maths Short Tricks in Quadratic Polynomials

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 27 : Graph of Quadratic Polynomials

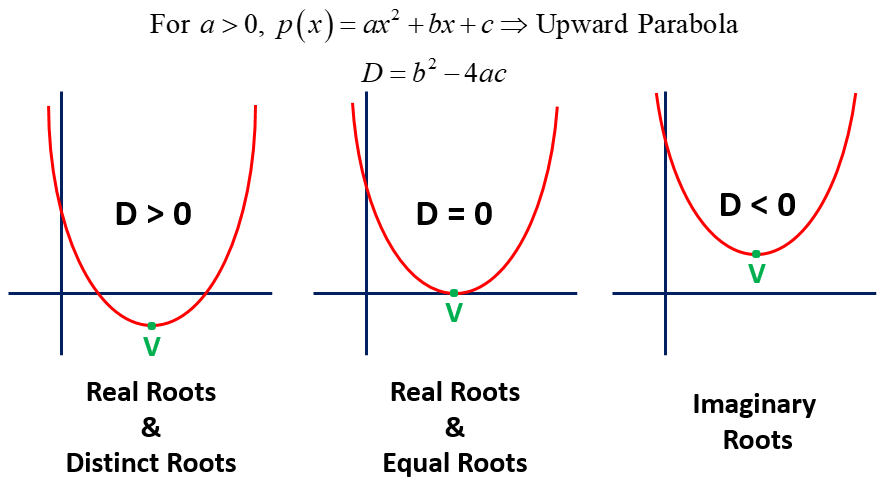
The graph of a quadratic polynomial y = p(x) = ax² + bx + c, is a parabola whose the coordinate of the vertex is V(-b/2a, -D/4a).

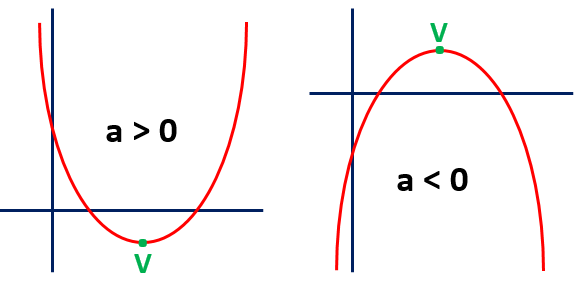
The parabola can be upward or downward, it depends on the sign of ‘a‘ (coefficient of x²).

If the sign of ‘a‘ (coefficient of x²) in the quadratic polynomial y = ax² + bx + c is positive, then the graph of the quadratic polynomial is an upward parabola.

In this case, the maximum and minimum values of the quadratic polynomial is as below.

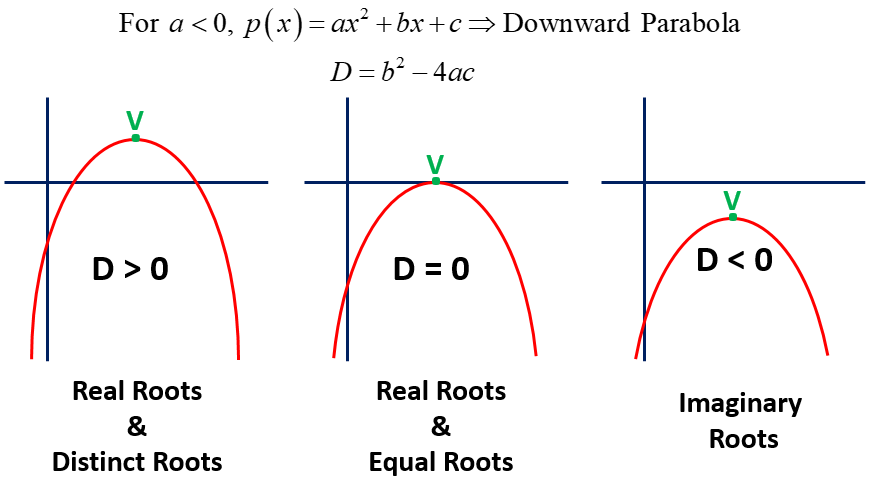
If the sign of ‘a‘ (coefficient of x²) in the quadratic polynomial y = ax² + bx + c is negative, then the graph of the quadratic polynomial is an downward parabola.

In this case, the maximum and minimum values of the quadratic polynomial is as below.

From the above graphs, we conclude that

If a > 0 and D < 0, then p(x) = ax² + bx + c > 0 for all real values of x.

If a < 0 and D < 0, then p(x) = ax² + bx + c > 0 for all real values of x.

Maths Short Trick 28 : Sign of a, b, c, D in p(x) = ax² + bx + c

We can also know the sign of a, b, c and D = b² – 4ac in the quadratic polynomial p(x) = ax² + bx + c by its graph.

Sign of a:

If the graph of the quadratic polynomial p(x) = ax² + bx + c is an upward parabola, then the sign of a is positive.

If the graph of the quadratic polynomial p(x) = ax² + bx + c is a downward parabola, then the sign of a is negative.

Sign of b:

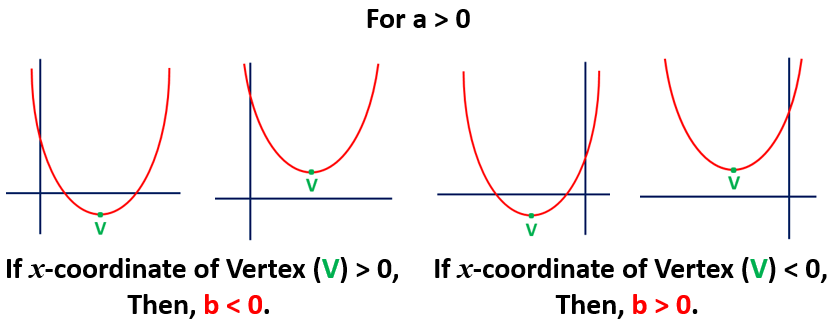
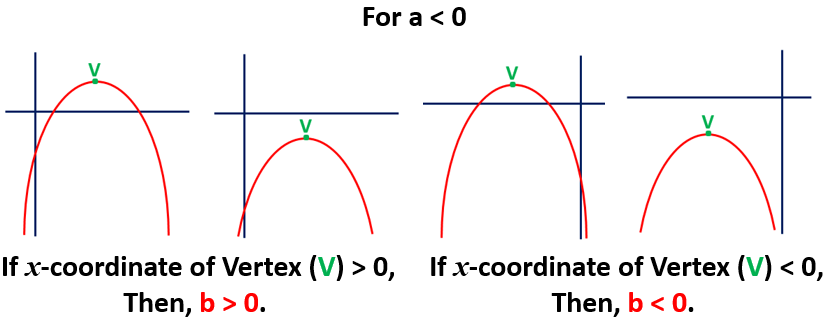
For the upward parabola (a > 0), then the sign of b in quadratic polynomial p(x) = ax² + bx + c is different sign of x-coordinate of vertex (V).

For the downward parabola (a < 0), then the sign of b in quadratic polynomial p(x) = ax² + bx + c is same sign of x-coordinate of vertex (V).

Sign of c:

The sign of c in quadratic polynomial p(x) = ax² + bx + c is same as the sign of y-intercept. For this, put x = 0 in y = p(x) = ax² + bx + c, we get the sign of c.

Sign of D = b² – 4ac:

If the graph of the quadratic polynomial p(x) = ax² + bx + c intersects x-axis, then D > 0.

If the graph of the quadratic polynomial p(x) = ax² + bx + c touches x-axis, then D = 0.

If the graph of the quadratic polynomial p(x) = ax² + bx + c does NOT intersect x-axis, then D < 0.

Maths Short Tricks in Linear Equations In Two Variables

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 29 : Standard Form of Linear Equations

The standard form of linear equations is

a₁x + b₁y + c₁ = 0 and

a₂x + b₂y + c₂ = 0.

These two equations can be solved by method of substitutions, equating the coefficients and cross multiplications.

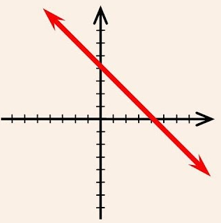
The graph of a the linear equation is a straight line.

Maths Short Trick 30 : Cross-Multiplication Method

The cross multiplication method for solving linear equations in two variables is as below.

Maths Short Trick 31 : Conditions of Solvability

The standard form of linear equations is

a₁x + b₁y + c₁ = 0 

a₂x + b₂y + c₂ = 0

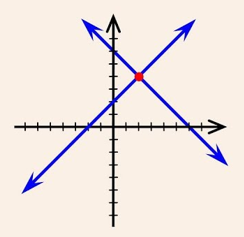
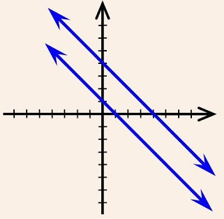
For Unique Solution (Only One Solution) or Consistent System of Equations, in this case the graph of the linear equations is intersected lines.

   

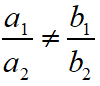
For No Solution or Inconsistent System of Equations, in this case the graph of the linear equations is parallel lines.

For Many Solution or Consistent System of Equations, in this case the graph of the linear equations is coincident lines.

Maths Short Trick 32 : Integer Solutions of Linear Equations

In the linear equation ax + by = n, if HCF (a, b) exactly divides n, then the integers solutions of x and y exist, otherwise NOT.

For the equation x₁ + x₂ + x₃ + … + x_r = n,

Maths Short Tricks in Quadratic Equations

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 33 : Quadratic Equations

The standard form of a quadratic polynomial is p(x) = ax² + bx + c. Then, ax² + bx + c = 0 is the general equation of quadratic equations, where a, b and c are real and a 0.

Since the degree of a quadratic equation is two, then the quadratic equation is satisfied by exactly two roots which may be real of imaginary.

A quadratic equation cannot have more than two roots. If a quadratic equation have more than two roots, then the quadratic equation becomes an identity. It is possible when a = b = c = 0 in ax² + bx + c = 0.

Maths Short Trick 34 : Roots of Quadratic Equations

The roots of the quadratic equation ax² + bx + c = 0 are 

Thus, the sum of the roots is α + β = -b/a and the product of the roots is αβ = c/a.

Maths Short Trick 35 : Nature of Roots of Quadratic Equations

In a quadratic equation ax² + bx + c = 0, the value D = b² – 4ac is known as discriminant of the quadratic equation.

The nature of the roots of the quadratic equation depends on the discriminant.

Case I: When D > 0

In this case, the roots α and β of the quadratic equation are real and unequal.

Case II: When D = 0

In this case, the roots α and β of the quadratic equation are real and equal.

Case III: When D < 0

In this case, the roots α and β of the quadratic equation are imaginary and distinct.

Case IV: When a, b and c are rational and D > 0 but NOT perfect square

In this case, the roots α and β of the quadratic equation are irrational and occurs in pairs.

Case V: When a, b and c are irrational and D > 0 but NOT perfect square

In this case, the roots α and β of the quadratic equation irrational and may not occurs in pairs.

Case VI: When a = 1 and b and c are integers and D is perfect square

In this case, the roots α and β of the quadratic equation are integers.

Maths Short Trick 36 : Common Roots of Quadratic Equations

For two quadratic equations a₁x² + b₁x + c₁ = 0 and a₂x² + b₂x + c₂ = 0.

If the two quadratic equations have both roots common, then the equations are identical and their coefficients are in proportions. It means,

If the two quadratic equations have only one root common (let α is common root of both equation), then the required condition can be found by these steps.

Maths Short Tricks in Arithmetic Progression

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 37 : General or nth Term of an AP

If the sequence t₁, t₂, t₃, …, t_n-1, t_n are in AP, then the general term of the AP is t_n = a + (n – 1)d, where a is the first term (a = t₁) and d is the common difference (d = t₂ – t₁ = t₃ – t₂ = … etc). 

Maths Short Trick 38 : nth Term of an AP from Last

Let a be the first term (a = t₁) and d be the common difference (d = t₂ – t₁ = t₃ – t₂ = … etc) of an AP having total N terms. Then, the n^th term from the end or last of the AP is the (N – n + 1)^th term from the beginning of the AP. 

Maths Short Trick 39 : Selection of Terms in AP

Three terms in AP are taken as (a – d), a, (a + d). In this, the common difference is d.

Four terms in AP are taken as (a – 3d), (a – d), (a + d), (a + 3d). In this, the common difference is 2d.

Five terms in AP are taken as (a – 2d), (a – d), a, (a + d), (a + 2d),. In this, the common difference is d.

Six terms in AP are taken as (a – 5d), (a – 3d), (a – d), (a + d), (a + 3d), (a + 5d). In this, the common difference is 2d.

Maths Short Trick 40 : Sum of n Terms of AP

Let a be the first term (a = t₁) and d be the common difference (d = t₂ – t₁ = t₃ – t₂ = … etc) of an AP having total n terms. Then, the sum of n terms of AP is 

If the last term or n^th term of the AP is known, then the sum of n terms of AP is

Maths Short Trick 41 : Arithmetic Mean

If three terms a, b, c are in AP, then b – a = c – b, then 2b = a + c or b = (a + c)/2.

Thus, one arithmetic mean between two numbers x and y is AM = (x + y)/2.

Now, let A₁, A₂, A₃, … A_n are n AMs between two number a and b.

Then, a, A₁, A₂, A₃, … A_n, b are in AP. Here, total number of terms is (n+2).

Thus, b = a + (n + 2 – 1)d or d = (b – a)/(n + 1).

Hence, the n arithmetic means between a and b are

A₁ = a + (b – a)/(n + 1), A₂= a + 2(b – a)/(n + 1), …, A_n = a + n(b – a)/(n + 1).

Maths Short Tricks in Geometric Progression

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 42 : General or nth Term of an GP

If the sequence t₁, t₂, t₃, …, t_n-1, t_n are in GP, then the general term of the GP is t_n = ar^(n-1), where a is the first term (a = t₁) and r is the common ratio (r = t₂ / t₁ = t₃ / t₂ = … etc). 

Maths Short Trick 43 : nth Term of a GP from Last

Let a be the first term (a = t₁) and r be the common ratio (r = t₂ / t₁ = t₃ / t₂ = … etc) of a GP having total N terms. Then, the n^th term from the end or last of the GP is the (N – n + 1)^th term from the beginning of the GP. 

Maths Short Trick 44 : Selection of Terms in GP

Three terms in GP are taken as a/r, a, ar. In this, the common ratio is r.

Four terms in GP are taken as a/r³, a/r, ar, ar³. In this, the common ratio is r².

Five terms in GP are taken as a/r², a/r, a, ar, ar²,. In this, the common ratio is r.

Maths Short Trick 45 : Sum of n Terms of GP

Let a be the first term (a = t₁) and r be the common ratio (r = t₂ / t₁ = t₃ / t₂ = … etc) of a GP having total n terms. Then, the sum of n terms of GP is

Maths Short Trick 46 : Sum of Infinite GP

Let a be the first term (a = t₁) and r be the common ratio such that |r| < 1 of a GP having infinite terms. Then, the sum of infinite GP is

Maths Short Trick 47 : Geometric Mean

If three terms a, b, c are in GP, then b / a = c / b, then b² = ac or b = (ac)^1/2 or b = √(ac), a > 0 and c > 0.

Thus, one geometric mean between two numbers x and y is GM = √(xy).

Now, let G₁, G₂, G₃, … G_n are n GMs between two number a and b.

Then, a, G₁, G₂, G₃, … G_n, b are in GP. Here, total number of terms is (n+2).

Thus, b = ar^{(n + 2 – 1)} or r = (b/a)^{1/(n + 1)}.

Hence, the n geometric means between a and b are

A₁ = a(b/a)^{1/(n + 1)}, A₂= a(b/a)^{2/(n + 1)}, …, A_n = a(b/a)^{n/(n + 1)}.

Maths Short Trick 48 : Relation Between AM, GM, HM

Let a₁, a₂, a₃, … an be n positive real numbers, then

If a₁ = a₂ = a₃ = … = a_n, then equality holds, means AM = GM = HM.

Maths Short Tricks in Trigonometry

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 49 : Degree & Radian

To convert an angle in degree into radian, we need to multiply π/180 to the degree.

For example: 30 degree = 30 x π/180 = π/6 radian.

To convert an angle in radian into degree, we need to multiply 180/π to the degree.

For example: π/6 radian = π/6 x 180/π = 30 degree.

Maths Short Trick 50 : Trigonometric Ratios

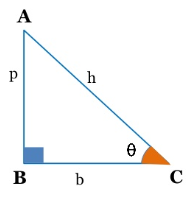
In trigonometry, we study the relation between the sides and angles of a right triangle. For this, six trigonometric ratios are defined as below.

1. sinθ = p/h = AB/AC        4. cosecθ or cscθ = h/p = AC/AB

2. cosθ = b/h = BC/AC       5. secθ = h/b = AC/BC

3. tanθ = p/b = AB/BC        6. cotθ = b/p = BC/AB

Using these definition of trigonometric ratios, some more trigonometric formulas are

7. tanθ = sinθ / cosθ           8. cotθ = cosθ / sinθ

9. sinθ x cosecθ = 1 or sinθ = 1/ cosecθ and cosecθ = 1/ sinθ

10. cosθ x secθ = 1 or cosθ = 1/ secθ and secθ = 1/ cosθ

11. tanθ x cotθ = 1 or tanθ = 1/ cotθ and cotθ = 1/ tanθ

Maths Short Trick 51 : Trigonometric Identities

Using Pythagorean theorem p² + b² = h² and the basic definition of trigonometric ratios, we get three trigonometric identities as below.

12. sin²θ + cos²θ = 1    13. sec²θ – tan²θ = 1    14. cosec²θ – cot²θ = 1

Using a² – b² = (a + b)(a – b) in sec²θ – tan²θ = 1, we get (secθ + tanθ)(secθ – tanθ) = 1. Thus, we get results as

15. secθ + tanθ = 1 / (secθ – tanθ) and 16. secθ – tanθ = 1 / (secθ + tanθ), where θ  nπ + π/2

Using a² – b² = (a + b)(a – b) in cosec²θ – cot²θ = 1, we get (cosecθ + cotθ)(cosecθ – cotθ) = 1. Thus, we get results as

17. cosecθ + cotθ = 1 / (cosecθ – cotθ) and 18. cosecθ – cotθ = 1 / (cosecθ + cotθ), where θ  nπ

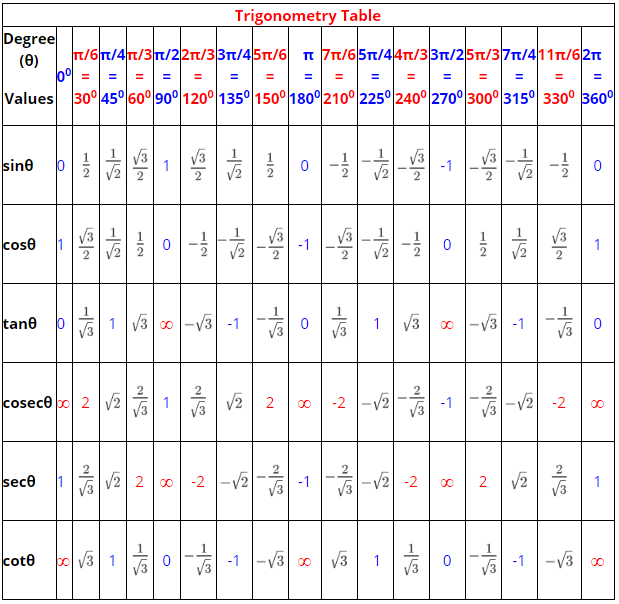
Maths Short Trick 52 : Trigonometric Tables

There are some specific trigonometric values of certain angles which are given below in trigonometric table.

Maths Short Trick 53 : Trigonometric Values

There are also trigonometric values of some important angles other than 0, 30, 45, 60, 90, 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, 330 and 360 degrees as given in above trigonometric table.

1. sin15^o = cos75^o = ,

2. cos15^o = sin75^o = ,

3. tan15^o = cot75^o = ,

4. cot15^o = tan75^o = , 

5. sin22.5^o = cos67.5^o = , 

6. cos22.5^o = sin67.5^o = ,

7. tan22.5^o = , 

8. cot22.5^o = ,

9. sin18^o = cos72^o = ,

10. cos18^o = sin72^o = ,

11. sin36^o = cos54^o = ,

12. cos36^o = sin54^o = ,

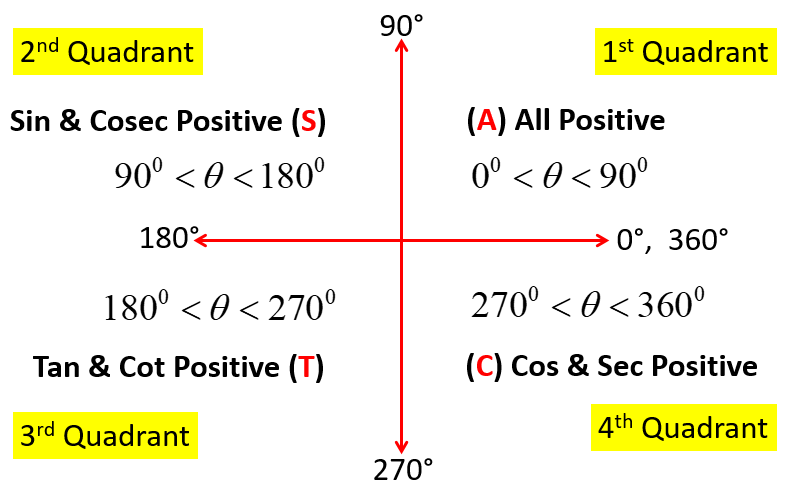
Maths Short Trick 54 : Sign of Trigonometric Ratios

The sign of the trigonometric ratios (sinθ, cosθ, tanθ, cosecθ, secθ, cotθ) depends on the angle θ in which it lies in the quadrants. For this, we use the concept of ASTC rule.

Maths Short Trick 55 : Allied Angles Formulas

The angles 90^o  θ, 180^o  θ, 270^o  θ and 360^o  θ are knwon as allied angles. The value of trigonometric ratios of these allied angles is according to the ASTC Rule as discussed above.

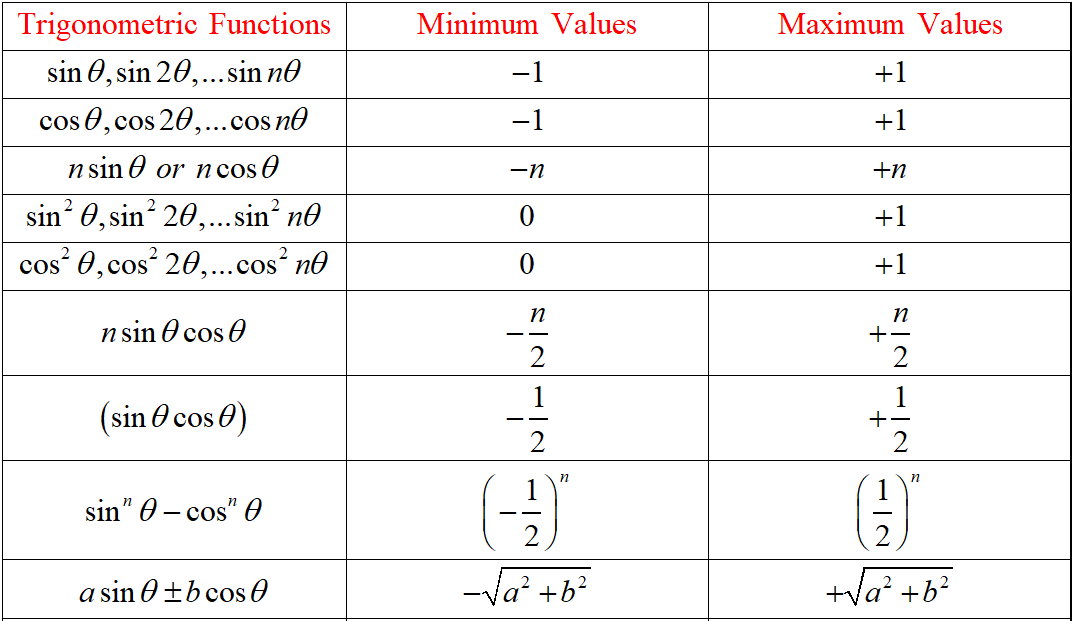
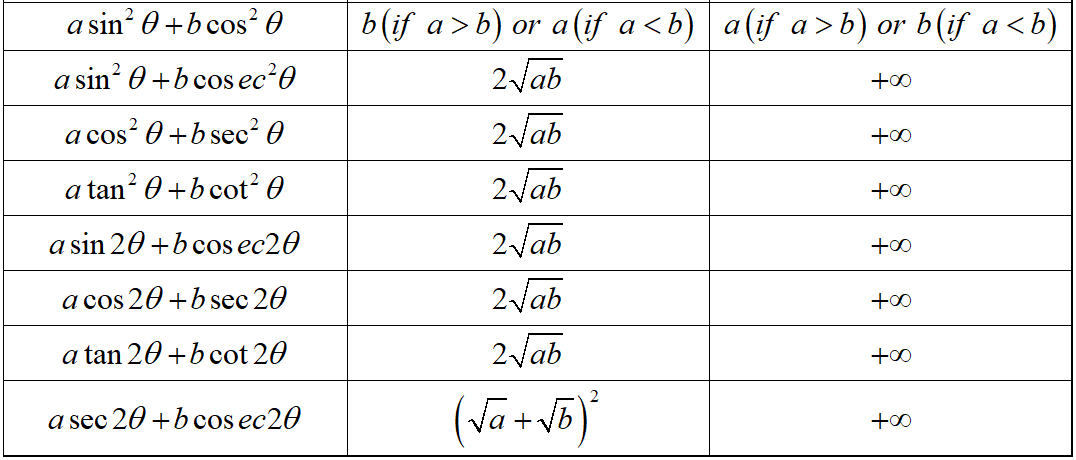
Maths Short Trick 56 : Maximum and Minimum Values of Trigonometric Functions

The maximum and minimum values of trigonometric functions are as below in table.

Maths Short Tricks in Coordinate Geometry

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

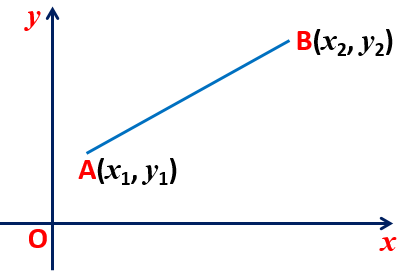
Maths Short Trick 57 : Distance Formula

The distance between the points A(x₁, y₁) and B(x₂, y₂) is |AB| = √[(x₂ – x₁)² + (y₂ – y₁)²]

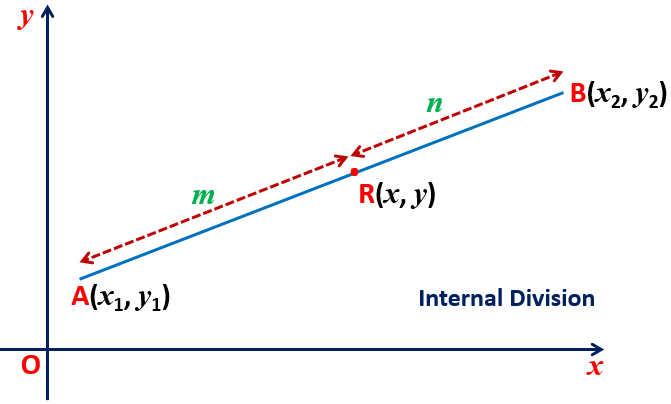
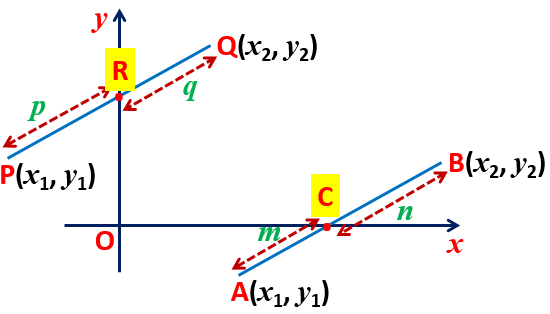
Maths Short Trick 58 : Section Formula

The coordinate of the points dividing the line segment joining the points A(x₁, y₁) and B(x₂, y₂) internally in the ratio of m:n is

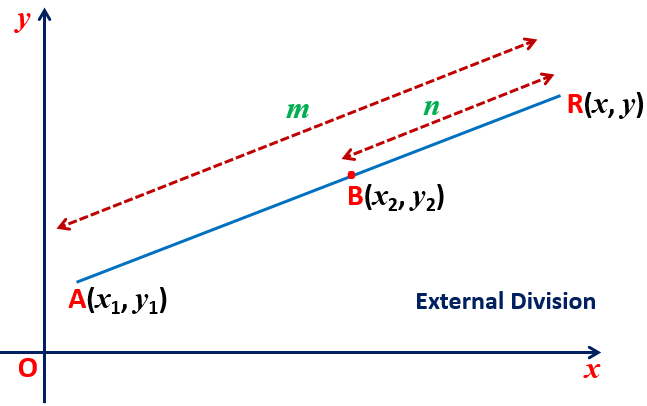
The coordinate of the points dividing the line segment joining the points A(x₁, y₁) and B(x₂, y₂) externally in the ratio of m:n is

Maths Short Trick 59 : Ratio in Section Formula

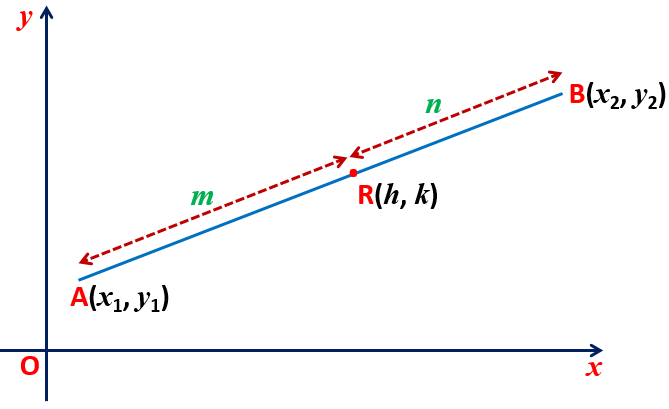
The point R(h, k) (if this is given) divides the segment joining the point P(x₁, y₁) and Q(x₂, y₂) in the ratio m : n = (x₁ – h) : (h – x₂) or m : n = (y₁ – k) : (k – y₂).

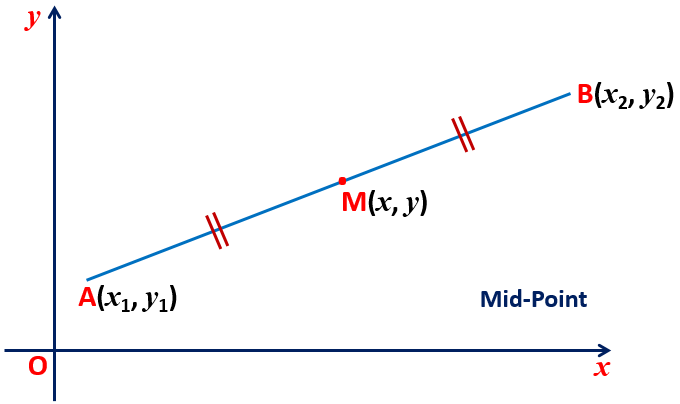
Maths Short Trick 60 : Mid Point Coordinates

The coordinate of the midpoints of the line segment joining the points A(x₁, y₁) and B(x₂, y₂) is

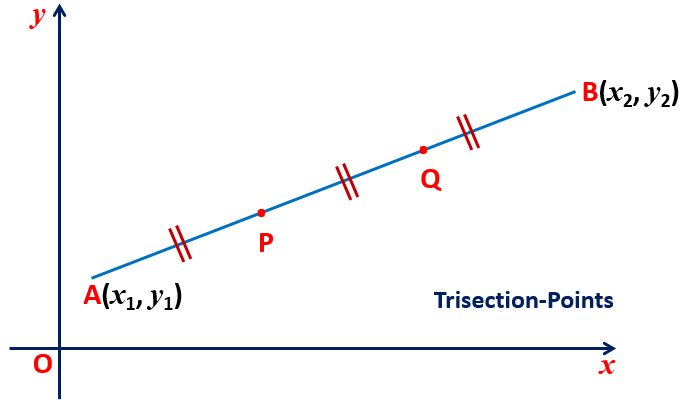
Maths Short Trick 61 : Trisection-Points Coordinates

The coordinate of the trisection points of the line segment joining the points A(x₁, y₁) and B(x₂, y₂) is

Maths Short Trick 62 : Division By Axes

x-axis divides the segment joining the points A(x₁, y₁) and B(x₂, y₂) in the ratio m:n = (-y₁ : y₂) and y-axis divides the segment joining the points P(x₁, y₁) and Q(x₂, y₂) in the ratio p:q = (-x₁ : x₂).

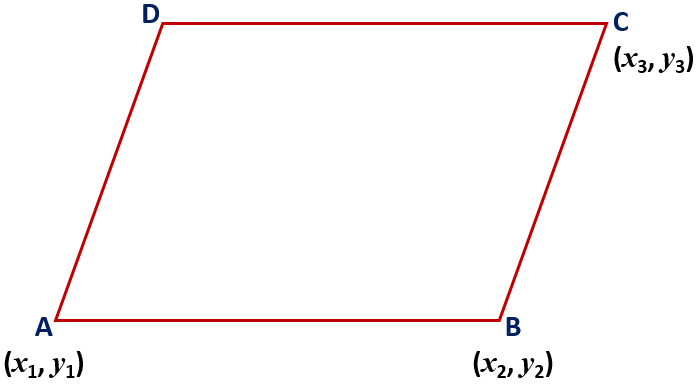
Maths Short Trick 63 : Fourth Vertex of Parallelogram

if three consecutive vertices of parallelogram ABCD are A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃), then the coordinates of fourth vertex is D{(x₁ – x₂ + x₃), (y₁ – y₂ + y₃)}.

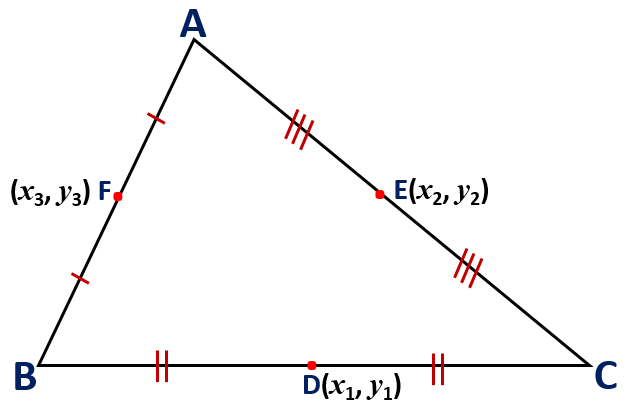
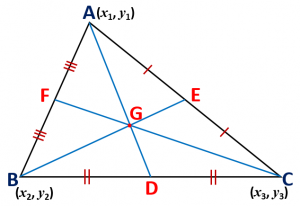
Maths Short Trick 64 : Vertices of Triangle

If D(x₁, y₁), E(x₂, y₂) and F(x₃, y₃), are the mid points of BC, CA and AB respectively, then the coordinates of the vertices of triangle ABC are

A(x₂ + x₃ – x₁, y₂ + y₃ – y₁),

B(x₁ + x₃ – x₂, y₁ + y₃ – y₂),

C(x₁ + x₂ – x₃, y₁ + y₂ – y₃), 

Maths Short Trick 65 : Right Angle Vertex of Right Triangle

If A(x₁, y₁) and B(x₂, y₂) are the coordinates of the hypotenuse of right angle triangle ABC, then the coordinate of right angle vertex C is

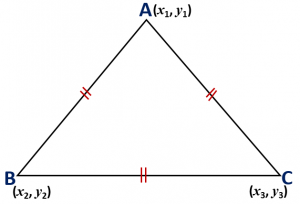
Maths Short Trick 66 : Third Vertex of Equilateral Triangle

If A(x₁, y₁) and B(x₂, y₂) are the coordinates of the two vertices of an equilateral triangle ABC, then the coordinate of third vertex C is

The coordinates of the vertices of an equilateral triangle cannot be rational.

Maths Short Trick 67 : Centroid of Triangle

If A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are the coordinates of the vertices of a triangle ABC, then the coordinate of centroid (intersection point of medians) is

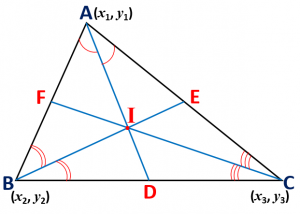
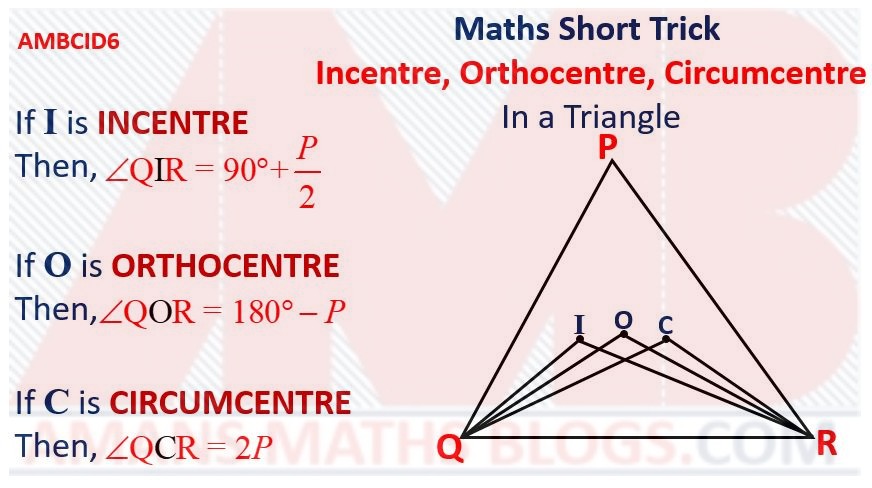
Maths Short Trick 68 : Incentre of Triangle

If A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are the coordinates of the vertices of a triangle ABC, then the coordinate of incentre (intersection point of angle bisectors) is

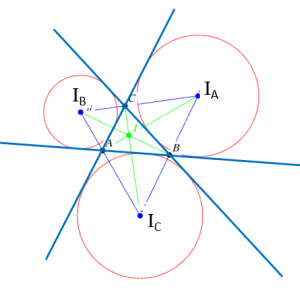
Maths Short Trick 69 : Excentre of Triangle

The internal angle bisector of one angle and external angle bisector of other two angles in the triangle are concurrent and the point of concurrency is called as excentre of triangle.

If A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are the coordinates of the vertices of a triangle ABC, then the coordinate of excentres are 

The incentre of triangle ABC is the orthocentre of triangle I_AI_BI_C.

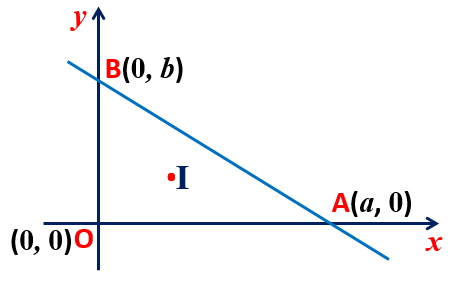
Maths Short Trick 70 : Incentre of Triangle OAB

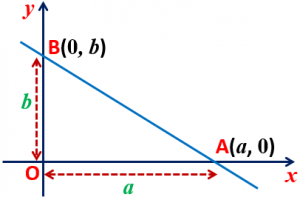
The coordinate of incentre of triangle formed by the points O(0, 0), A(a, 0) and B(0, b) are

Maths Short Trick 71 : Orthocentre & Circumcentre

The orthocentre of right triangle is at the vertex of the right angle.

The circumcentre of right angled triangle is at the mid-point of hypotenuse.

In an equilateral triangle, the orthocentre, circumcentre, centroid and incentre coincide.

For any triangle, Orthocentre, Centriod, Circumcentre are collinear and orthocentre divides the line joining the centroid and circumcentre in the ratio 1 : 2.

Maths Short Trick 72 : Area of Triangle

The area of triangle whose coordinates are A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) then

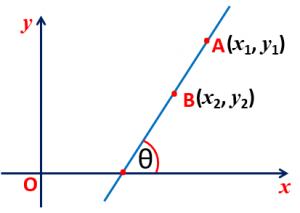
Maths Short Trick 73 : Slope of Line

The slope of line making an angle θ is m = tanθ.

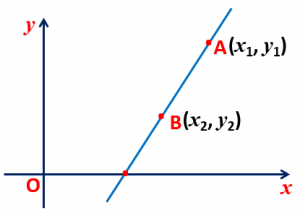
The slope of line passing through A(x₁, y₁) and B(x₂, y₂) is m = (y₂ – y₁)/(x₂ – x₁).

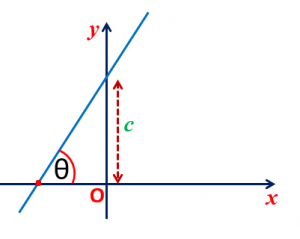
Maths Short Trick 74 : Equation of Straight line

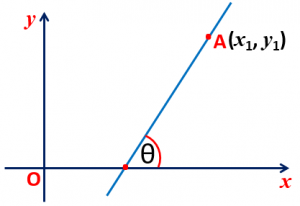
Slope Intercept Form: If a line makes an angle θ with x-axis in positive direction and making an intercept length ‘c‘ on y-axis, then the equation of line is y = mx + c, where m = tanθ.

Point Slope Form: If a line makes an angle θ with x-axis in positive direction and passing through the point A(x₁, y₁), then the equation of line is y – y₁ = m(x – x₁), where m = tanθ.

Two Points Form: If a line passes through the point A(x₁, y₁) and B(x₂, y₂), then the equation of line is (y – y₁)/(y₁ – y₂) = (x – x₁)/(x₁ – x₂).

Intercept Form: If a line makes intercepts ‘a‘ and ‘b‘ on x-axis and y-axis respectively, then the equation of line is x/a + y/b = 1.

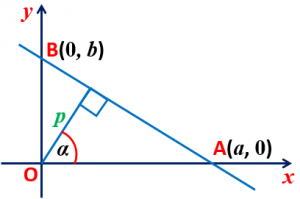
Normal Form: The equation of straight line upon which the length of perpendicular from origin is ‘p’ and the perpendicular makes an angle ‘α‘ with x-axis is xcosα + ysinα = p.

Maths Short Trick 75 : Angle Between Lines

If y = m₁x + c₁ and y = m₂x + c₂ are two equations of straight lines, then the angle between two lines is 

If a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 are two equations of straight lines, then the angle between two lines is

Maths Short Trick 76 : Parallel Lines

If the lines y = m₁x + c₁ and y = m₂x + c₂ are parallel, then m₁ = m₂.

If the lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 are parallel, then a₁ / a₂ = b₁ / b₂.

The equation of a line parallel to the line ax + by + c = 0 is ax + by + k = 0, the value of k can be found by the given condition in the question.

Maths Short Trick 77 : Perpendicular Lines

If the lines y = m₁x + c₁ and y = m₂x + c₂ are perpendicular, then m₁m₂ = -1.

If the lines a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 are perpendicular, then a₁a₂ + b₁b₂ = 0.

The equation of a line perpendicular to the line ax + by + c = 0 is bx – ay + k = 0, the value of k can be found by the given condition in the question.

Maths Short Trick 78 : Collinear Points

Three points A, B and C are called to be collinear if they lie on the same line.

There are following methods can be used to check collinearity of three points:

Method 1 : Area of triangle ABC = 0.

Method 2 : Sum of any two of AB, BC and AC is equal to the third.

Method 3 : The equation of line passing through any two points (let A and B) through third point (C).

Method 4 : Slopes of lines joining the points are equal.

Method 5 : One point (let A) divides the other two (B and C) internally or externally.

Maths Short Tricks in Lines & Angles

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 79 :Basic Definition

Lines Angles Basic Definitions
Right Angle: θ = 90°	Straight Angle: θ = 180°
Acute Angle: 0° < θ < 90°	Obtuse Angle: 90° < θ < 180°
Complementary Angles: A + B = 90°	Supplementary Angles: A + B = 180°

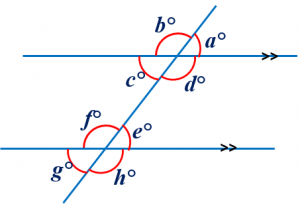
Maths Short Trick 80 :Transversal Lines

When a transversal line intersects two parallel lines, then:

Corresponding Angles are equal, a° = e°, b° = f°, c° = g°, d° = h°.

Alternate Interior Angles are equal, c° = e°, d° = f°.

Co-Interior Angles are Supplementary, d° + e° = 180°, c° + f° = 180°.

Maths Short Trick 81 :Polygons

The sum of all the interior angles of a convex polygon of n sides is (2n – 4) right angles or (n – 2) x 180 degree.

The sum of all the exterior angles of convex polygon is 360 degree.

Each interior angle of n-sided regular polygon is [(n – 2) x 180] / n.

Each intetrior angles of a regular polygon of n sides is (360 / n) degree.

If a polygon as n sides, then the number of diagonals of the polygon = n(n – 3)/2

Read More : More Details on Lines & Angles & Polygons

Maths Short Tricks in Triangles

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 82 :Basic Definition

Triangles Basic Definitions
Scalene Triangle: No Two Sides are Equal	Right Triangle: One Angle = 90°
Isosceles Triangle: Two Sides are Equal	Acute Triangle: All Angles < 90°
Equilateral Triangle: All Sides are Equal	Obtuse Triangle: One Angle > 90°

Read More : Properties of Isosceles Triangles

Maths Short Trick 83 : Angles Results

The sum all interior angles of a triangle is 180 degree.

If one side of the triangle is produced, then the exterior angle so formed is equal to the sum of two interior opposite angles. This exterior angle is greater than either of the interior opposite angles.

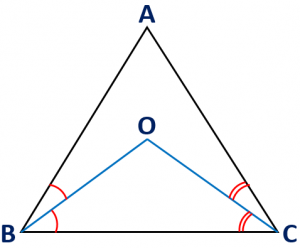
If the bisectors of angles ABC and ACB of a triangle ABC meet at a point O, then 

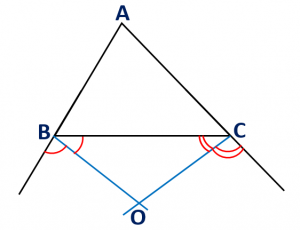
If the sides AB and AC of a triangle ABC are produced, then the angle between the bisectors of exterior angle of B and C intersecting at O is

Read More : Some More Results of Angles in Triangle

Maths Short Trick 84 : Triangle Inequalities

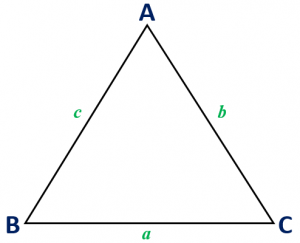
For any triangle ABC, AB = c, BC = a and CA = b. 

If two sides of a triangle are unequal, then longer side has greater angle opposite to it. In triangle ABC, if a > b, then angle A > angle B.

The sum of any two sides of a triangle is greater than its third side. In triangle ABC, (i) a + b > c, (ii) b + c > a, (iii) c + a > b.

The difference of any two sides of a triangle is less than its third side. In triangle ABC, (i) a – b < c, (ii) b – c < a, (iii) c – a < b.

In a right angled triangle, the sum of squares of two smaller sides is equal to the square of its third side. OR, In triangle ABC, if a² + b² = c², then ABC is a right angled triangle with angle C is 90 degree.

In an acute angled triangle, the sum of squares of two smaller sides is greater than the square of its third side. OR, In triangle ABC, if a² + b² > c², then ABC is an acute angled triangle.

In an obtuse angled triangle, the sum of squares of two smaller sides is smaller than the square of its third side. OR, In triangle ABC, if a² + b² < c², then ABC is an obtuse angled triangle with angle C is obtuse.
Read More : Some More Results of Triangle Inequalities

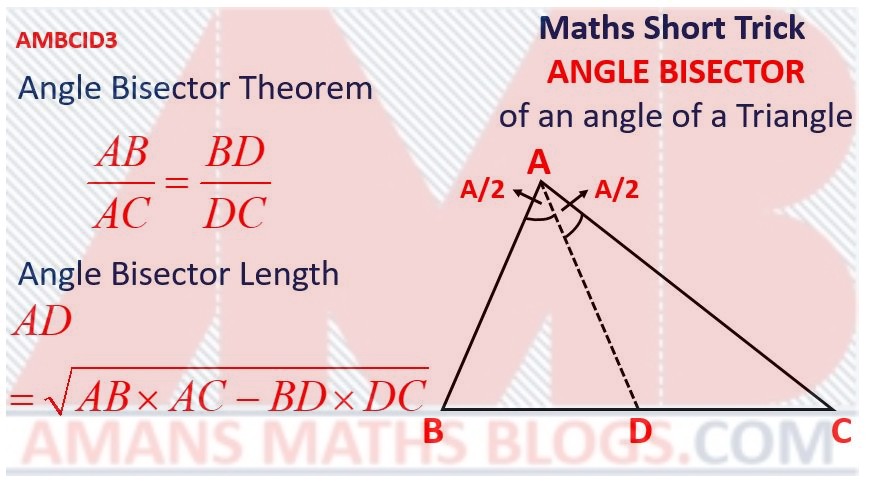
Maths Short Trick 85 : Length of Angle Bisector

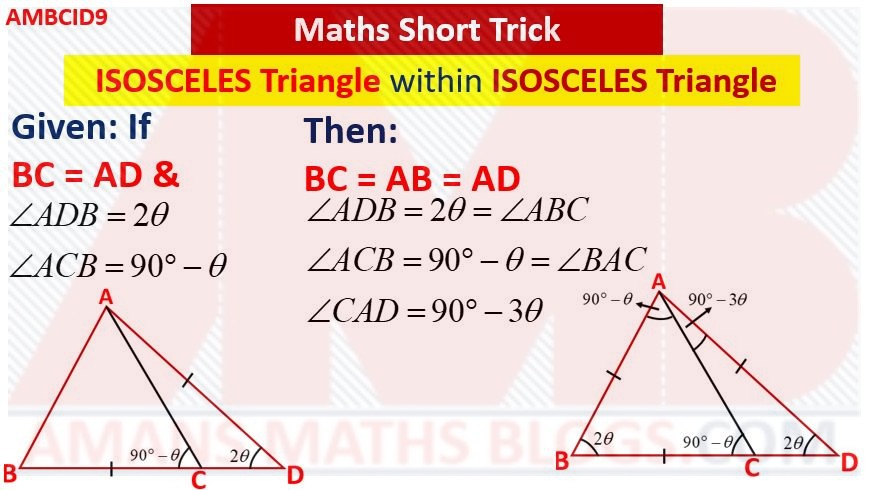
Maths Short Trick 86 : Isosceles Triangle Within Isosceles Triangle

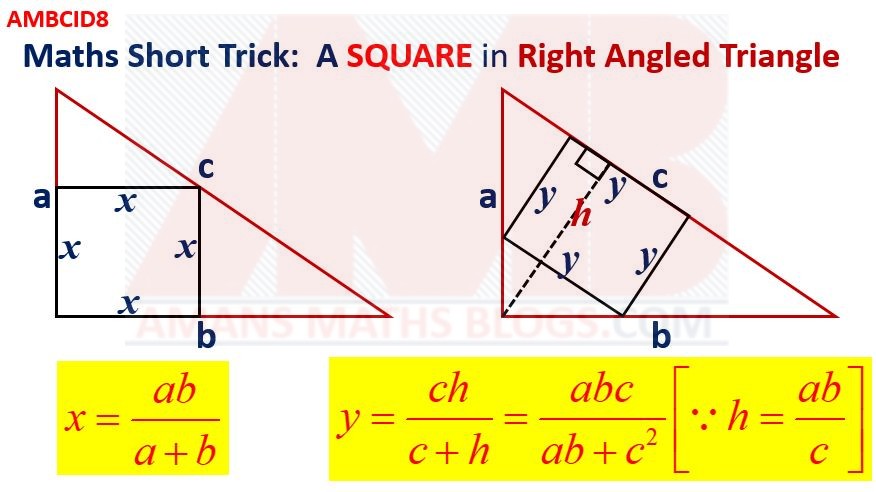
Maths Short Trick 87 : Square within Right Triangle

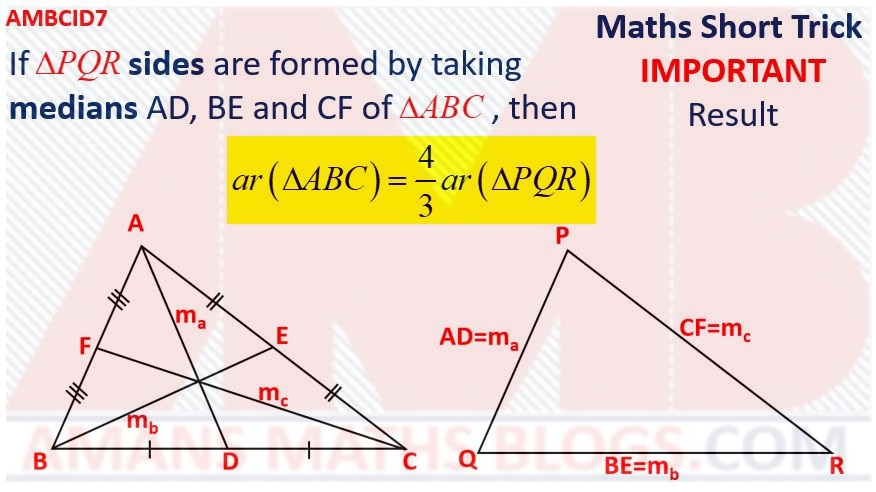
Maths Short Trick 88 : Triangle Formed by Medians

Maths Short Trick 89 : Centers of Triangle

Maths Short Tricks in Congruent Triangles

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

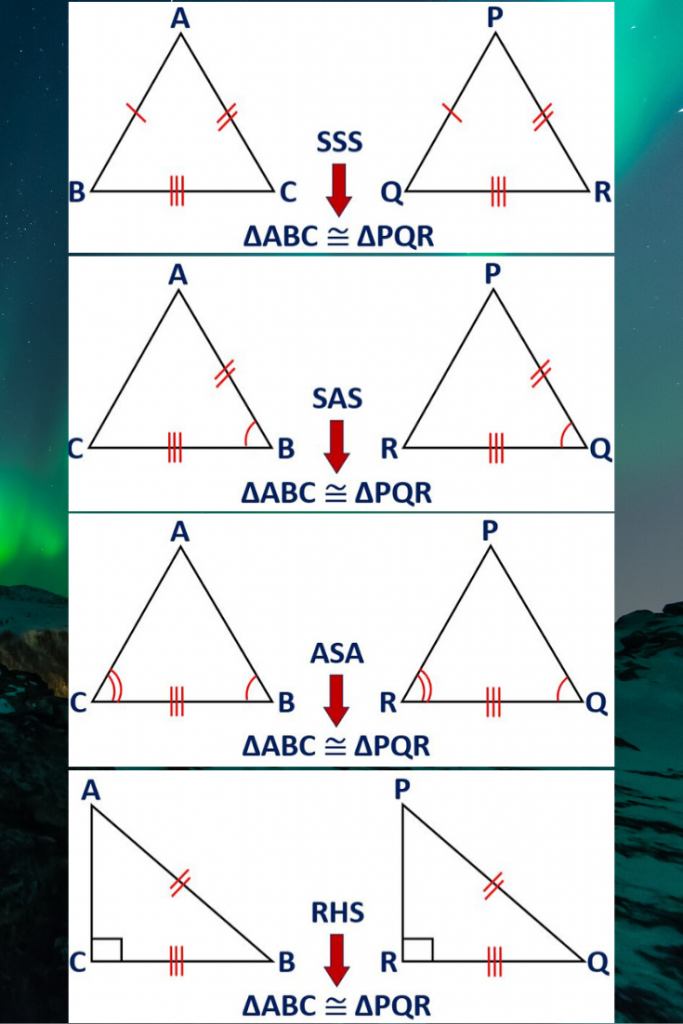
Maths Short Trick 90 :Congruence Criteria

The sufficient conditions for congruence criteria are as below:

Congruent Triangles Criteria
SSS	Three sides of one triangle are equal to the corresponding three sides of other triangle.
SAS	Two sides and the included angle of one triangle are equal to the corresponding two sides and the included angle of other triangle.
ASA	Two angles and the included side of one triangle are equal to the corresponding two angles and the included side of other triangle.
RHS	Hypotenuse and one side of one right triangle are equal to the hypotenuse and one side of other right triangle.

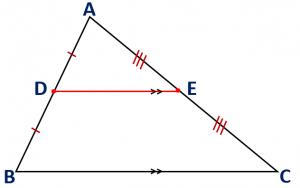
Maths Short Trick 91 : Mid Point Theorem

The line joining the mid points of any two sides of a triangle is parallel to the third side and half of it.

In triangle ABC, D and E are mid points of AB and AC respectively, then DE || BC and DE = BC/2.

Read More : Some Applications of Mid Point Theorem

Maths Short Tricks in Similar Triangles

Maths Short Trick 92 :Similarity Criteria

Similar Triangles Criteria
SSS	The corresponding sides of two triangles are proportional.
SAS	One pair of corresponding sides are proportional and the included angles are equal.
AA	Two triangles are equiangular.

Read More : Important Results Using Similar Triangles

Maths Short Trick 93 : Pythagorus Theorem

In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

In right triangle ABC with C = 90 degree, AB² = AC² + BC².

Read More : Learn Direct Results Using Pythagorus Theorem

Maths Short Tricks in Quadrilaterals

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

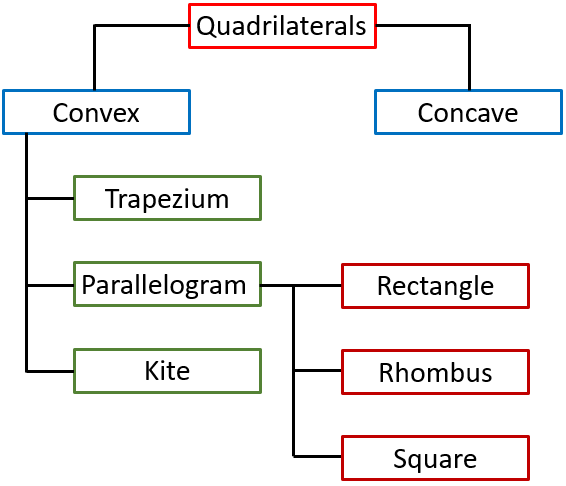
Maths Short Trick 94 : Basic Definitions

First, you need to understand types of quadrilaterals.

Read More : Properties of Parallelogram, Rectangles, Square

Maths Short Trick 95 : Cyclic Quadrilaterals

If ABCD is a cyclic quadrilateral, then the sum of opposite angles is 180 degrees. It means, ∠A + ∠C = ∠B + ∠D = 180 degrees.

Product of Diagonals: In a cyclic quadrilateral, the sum of product of two pairs of opposite sides equals the product of two diagonals. This property of cyclic quadrilateral is known as PTOLEMY THEOREM. If ABCD is a cyclic quadrilateral, then AB x CD + AB x BC = AC x BD.

Product of Diagonals: In a cyclic quadrilateral, the ratio of the diagonals equals the ratio of the sum of products of sides that share the diagonal’s end points.

If ABCD is a cyclic quadrilateral, then .

Read More : Proof Of These Two Theorems

Maths Short Tricks in Circles

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

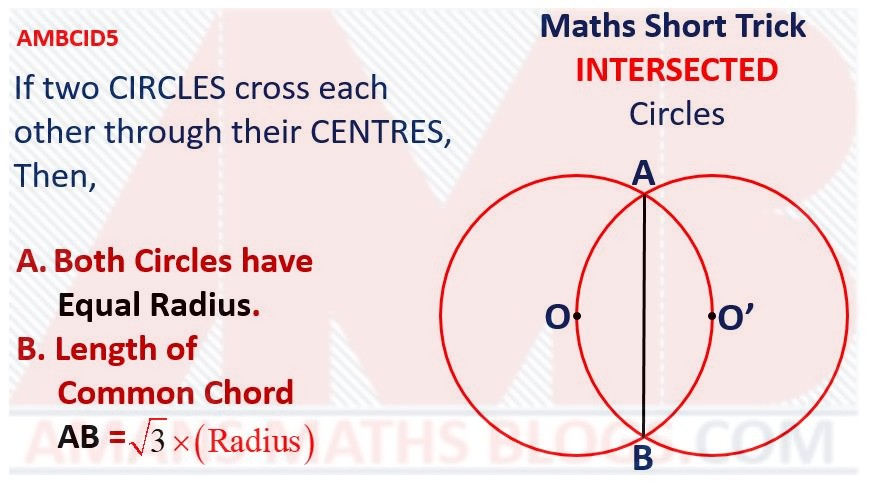
Maths Short Trick 96 : Length of Common Chord

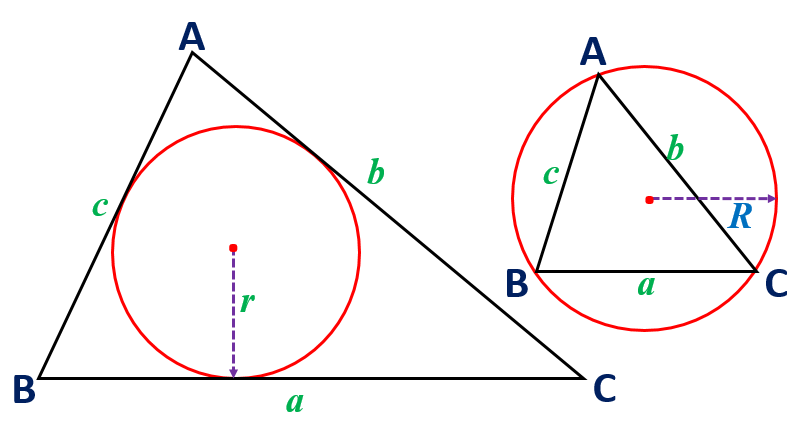
Maths Short Trick 97 : Circum-Radius & Inradius

If a triangle is inscribed in a circle, then the circumradius

R = (Product of Sides)/[4(Area of Triangle)].

If a circle is inscribed in a triangle, then the inradius

r = (Area of Triangle)/(Semi-Perimeter).

Read More : Learn More About Circle Related Concepts

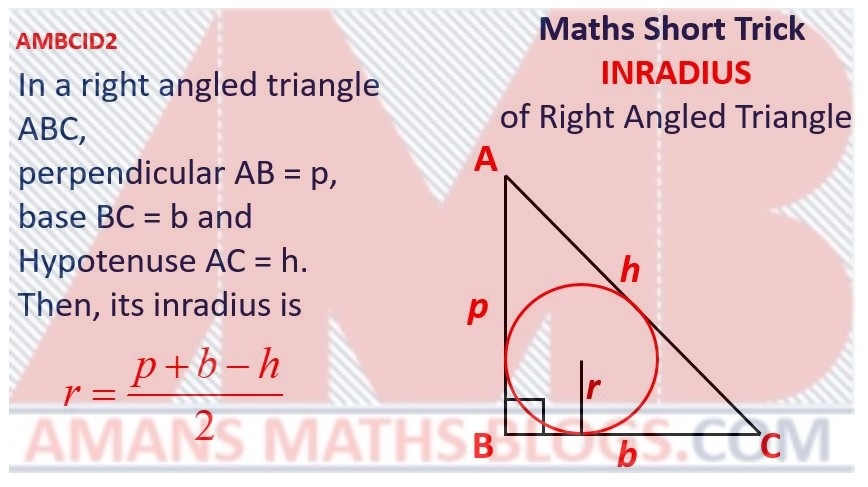
Maths Short Trick 98 : Circum-Radius & Inradius

Maths Short Tricks in Mensuration

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 99 : Area of Triangles

When the base and the height of a triangle are given, then

When all the lengths of sides of a triangle are given, then

where s = (a + b + c)/2

When two sides and included angle of a triangle are given, then

When the triangle is a right triangle, then

When the triangle is an equilateral triangle, then

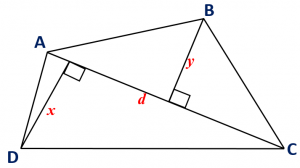
Maths Short Trick 100 : Area of Quadrilateral

In a quadrilateral, when the lengths of one diagonal and perpendiculars drawn on the diagonals are given, then

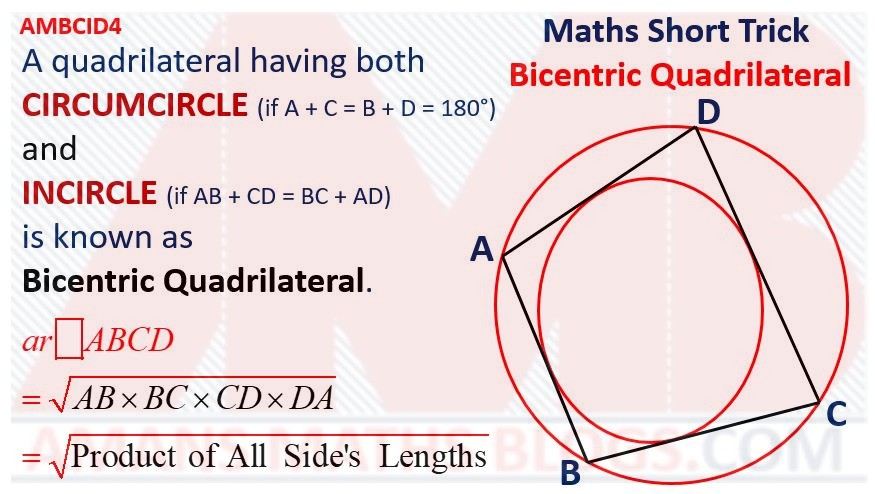
Maths Short Trick 101 : Bicentric Quadrilateral

Maths Short Trick 102 : Area of Parallelograms

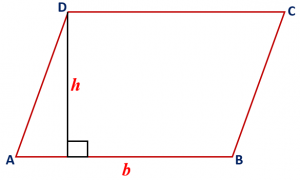
The area of a parallelogram is

Maths Short Trick 103 : Area of Rectangle

The area of a rectangle is

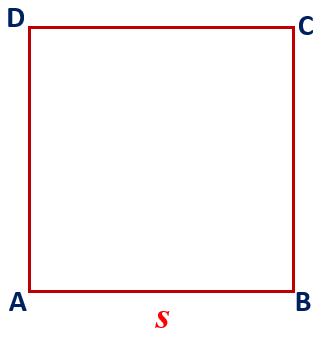
Maths Short Trick 104 : Area of Squares

The area of a square is

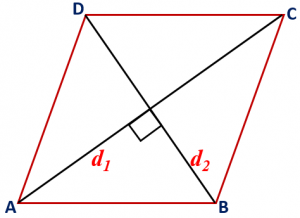
Maths Short Trick 105 : Area of Rhombus

The area of a rhombus is

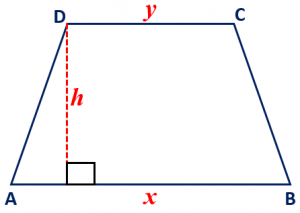
Maths Short Trick 106 : Area of Trapezium

The area of a trapezium is

Maths Short Trick 107 : Area of Circle

The area of a circle with radius r is

The area of a sector of a circle with radius r is

Maths Short Tricks in Surface Area & Volume

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

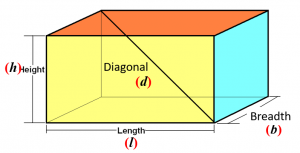
Maths Short Trick 108 : Cuboid

There are following formulas for cubiod: 

Lateral Surface Area is

Total Surface Area is

Volume is

Diagonal is

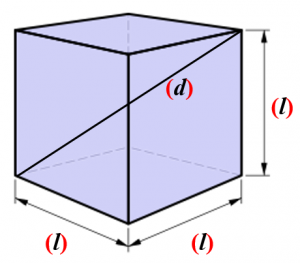
Maths Short Trick 109 : Cube

There are following formulas for cube (l = b = h):

Lateral Surface Area is

Total Surface Area is

Volume is

Diagonal is

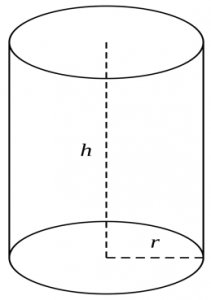
Maths Short Trick 110 : Cylinder

There are following formulas for cylinder:

Curved Surface Area is

Total Surface Area is

Volume is

Maths Short Trick 111 : Cone

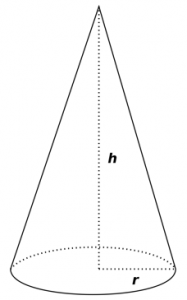
There are following formulas for cone:

Curved Surface Area is

Total Surface Area is

Volume is

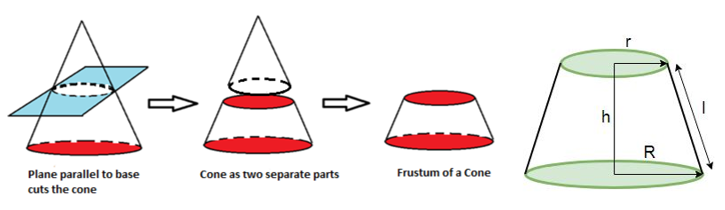
Maths Short Trick 112 : Frustum of Cone

There are following formulas for frustum of cone:

Curved Surface Area is

Total Surface Area is

Volume is

Maths Short Trick 113 : Sphere

There are following formulas for sphere:

Surface Area is

Volume is

To get the GEOMETRICCKS EBook, Click Image Below.

Maths Short Tricks in Statistics

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 114 : Mean Formulas

Arithmetic Mean of Unclassified Data : If n numbers be x₁, x₂, x₃, …, x_n, then the arithmetic mean of these unclassified data is

Arithmetic Mean of Frequency Distribution : If f₁, f₂, f₃, …, f_n, be the frequency of n numbers x₁, x₂, x₃, …, x_n, then the arithmetic mean of these frequency distribution is

Arithmetic Mean of Classified Data :To find the mean of a classified data, we first find class marks x₁, x₂, x₃, …, x_n, of the class intervals as the variables and take the frequencies of the classes f₁, f₂, f₃, …, f_n, as the corresponding frequencies of the variables. Then, the arithmetic mean of these classified data is

Deviation of a Term :The deviation of a term from the arithmetic mean is the quantity by which that term exceeds the arithmetic mean. If the variable be x and AM be A, then AM (x – A) is the deviation of x from A. Thus, the deviation is d = x – A.

Short Cut Method of Arithmetic Mean for Simple Distribution : The arithmetic mean of n simple distribution when the assumed mean (a) and deviation d = x – A is given is

Short Cut Method of Arithmetic Mean for Frequency Distribution : The arithmetic mean of  frequency distribution when the assumed mean (a) and deviation d = x – A is given is

Step Deviation Method for Arithmetic Mean : The step deviation method for arithmetic mean is where ‘a’ is assumed mean and u = (x_i – A)/h 

Combined Arithmetic Mean :If r collections of observations have arithmetic means A₁, A₂, A₃, … A_r whose total frequencies are n₁, n₂, n₃…, n_r respectively, then the combined mean is

Weighted Mean :If w be the weight of the variables x then the weighted mean is

Maths Short Trick 115 : Median Formulas

Median of Simple Distribution : First, we arrange the terms in ascending or descending order and then find the number of terms.

If ‘n’ is odd, then the median is

If ‘n’ is even, then the median is

Median of Continuous Distribution : If in a continuous distribution the total frequency be N then the class whose commutative frequency is either equal to N/2 of just greater than N/2 is called the median class

The median of continuous distribution is 

where

l = Lower limit of median class

f = Frequency of median class

N = Total Frequency

CF = Cumulative Frequency of class just before median class 

h = Class size of median class

Maths Short Trick 116 : Mode Formulas

Mode of Unclassified Distribution : In unclassified distribution, the mode is the data with highest frequency.

Mode of Continuous Distribution : The class with highest frequency is the mode class.

The mode of continuous distribution is

where

l = Lower limit of mode class

f = Frequency of mode class

f_-1 = Frequency of pre-mode class

f_-1 = Frequency of post-mode class

h = Class size of mode class

Maths Short Trick 117 : Relation Between Mean, Median & Mode

The relation between mean, median and mode is Mode = 3Median – 2Mean.

Maths Short Tricks in Permutation & Combination

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 118 : Multiplication Theorem

If a work is divided into a number of ‘n’ subworks that can be done by m₁, m₂, m₃, …m_n ways independently, then the work is completed when each subwork is completed. Thus, the total number of ways in completing the work is

Maths Short Trick 119 : Addition Theorem

If there is a number of independent work and we have to perform one of them, then the number of completing any one of the subwork by m₁, m₂, m₃, …m_n ways then the total number of ways of completing the work is

Maths Short Trick 120 : Permutation Formulas

Number of permutation of n different things taken r at a time (Number of ways of arranging r different things out of n different things) is

Number of ways of arranging all of n different things is

The number of ways of arranging n different things out of which p are alike and are of one type and q are alike and are of second type and rest are different is

The number of permutation of n different things taken r at a time, when each may be repeated any number of times in each arrangement is 

Maths Short Trick 121 : Cyclic Permutation Formulas

Number of ways of arranging n different things along a circle when clockwise and anticlockwise arrangements are different is

Number of ways of arranging n different things along a circle when clockwise and anticlockwise arrangements are same is

Maths Short Trick 122 : Combination Formulas

Number of ways of selecting r different things out of n different things is

Maths Short Trick 123 : Comparison Between Permutation & Combination

In combination, only selection is taken whereas in a permutation, both selection and arrangement are taken.

In combination, the order of the selected object is NOT considered. In permutation, the ordering is important. For example: (AB) and (BA) are same as in combination but it is different in permutation.

Permutation & Combination formulas comparison is

Maths Short Tricks in Probability

You can download this Maths Short Tricks for NTSE NSEJS JSTSE Exams as PDF, downloading link is at last.

Maths Short Trick 124 : Basic Definitions

Probability : Probability theory is that branch of mathematics in which we numerically study the chances of occurrence of events.

Experiment : An experiment is an activity which ends in a well defined result.

Trial : Performing an experiment one is called a trial.

Outcome : Result of a trial is called outcome.

Sample Space : The set of all possible outcomes of a random experiment is called sample space.

Events : A subset of sample space of a random experiment is called an event.

Elementary Events : Single element subset of sample space associated with a random experiment are known as the elementary events.

Compound Events : A subset of sample space which contains more than one element is called compound events.

Exhaustive Number of Cases  : The total number of elementary events of a random experiment is called the exhaustive events.

Mutually Exclusive Events : Events are mutually exclusive if the occurrence of any one of them prevent the occurrence of all of the other events. No two or more of them can occur simultaneously. 

Independent Events : Two or more events are said to be independent if the occurrence or non-occurrence of any of them does not affect the probability of occurrence or non-occurrence of any of them.

Maths Short Trick 125 : Probability Formulas

If E is the occurrence of any event and S is the total outcomes in sample space, then the probability of occurrence of event E is 

Some basic results of probability are:

Maths Short Trick 126 : Odds in Favour & Odds Against

Odds in Favour : Odds in favour of event E is

Odds Against : Odds against of event E is

If odds in favour of event E is m : n, then

If odds against of event E is m : n, then

Maths Short Trick 127 : Addition Theorem of Probability

The addition theorem of probability for two events A and B is

If A and B are mutually exclusive events, then

Similarly, the addition theorem of probability for three events A, B and C is

If A, B and C are mutually exclusive events, then

Maths Short Trick 128 : Conditional Probability

Let A and B are any two events, B s, then

P(A/B) : It denotes the conditional probability of occurrence of event A when B has already occurred. In this case P(A/B), B works as sample space and works as an event.

P(B/A) : It denotes the conditional probability of occurrence of event B when A has already occurred. In this case P(B/A), A works as sample space and works as an event.

Maths Short Trick 129 : Multiplication Theorem of Probability

If A and B two independent events, then

If A and B two dependent events, then

If A and B two mutually exclusive events, then

NTSE Maths Combo Pack EBook

Get 900+ NTSE Maths Previous Year Question Bank with Solutions and 11 Mock Test Papers EBook for NTSE exams. For more details, Click To NTSE Stage 1 Mock Test SAT Maths and NTSE Stage 2 Mock Test SAT Maths. To get this combo ebook, click below RED button.

900+ Math Questions Bank & 11 Mock Test Paper for NTSE Stage 1 & 2 SAT (Maths)

amans maths blogscbse examcoordinate geometry tricksgeometry short tricksjstse exammath short trickmaths short tricksmensuration tricksnsejs examNTSE Examntse mathsnumber system short trickspdf downloadpdf free downloadprobability short trickstrigonometry short tricks