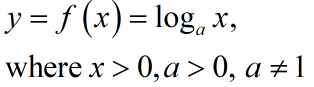Hi students, I am AMAN RAJ and welcome to AmansMathsBlogs (AMB). I am a MATH faculty in a reputed IIT Foundation Training Institute. I teach Maths to the students of class 8^th to 12^th. In mathematics, there are two topics named as exponential and logarithmic functions, which creates a lot of confusion to the students. So, the students, your confusion about the exponential and logarithmic functions will be cleared on this page.

Exponential and Logarithmic Functions Doubts

During the class, when I ask some concepts about the exponential and logarithmic functions to the students, I found that the students have the following doubts of regarding exponential and logarithmic functions.

Doubt 1: The function f(x) = 0^x is NOT an exponential function.

Doubt 2: The function g(x) = 1^x is NOT an exponential function.

Doubt 3: The function h(x) = (–2)^x is NOT an exponential function.

Doubt 4: Why the base of logarithm cannot be negative, means a > 0?

Doubt 5: Why the base of logarithm cannot be unity, means a ≠ 1?

Doubt 6: Why logarithm of any negative number is not defined, mean log(–2) is not defined?

So the students, keep reading this article about the exponential and logarithm carefully. I will clear your all the above doubts.

First, we start from the exponential function in details.

As we know that the exponential function is in the form of

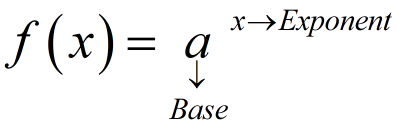
For example, y = 2^x, y = (1/2)^x etc. These are the exponential function. 

Now, most of the students are in misconception that the functions are as below.

They assume that these above function are also an example of exponential function, because these look like the general form of the exponential function as f(x) = a^x.

But, the students, your concepts that these above functions are the exponential function is wrong.

Now, the students are curious about to know that:

Why are these functions NOT exponential functions?

What are the reasons that these are not considered as the exponential functions? 

To know about the reasons, first we need to understand the properties of the general for the exponential function f(x) = a^x. 

Properties of Exponential Functions

There are following properties about the exponential function.

Property 1:

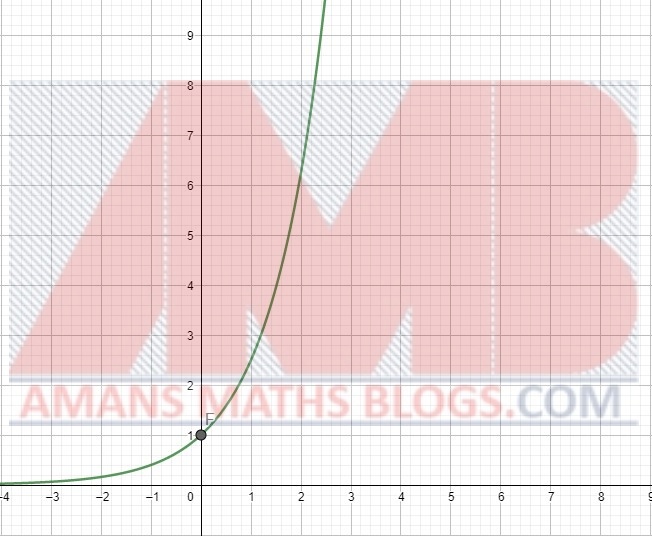
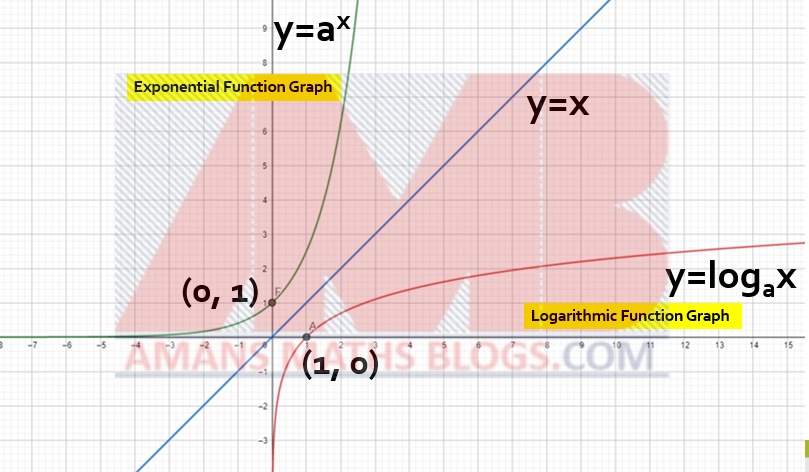
If we put x = 0 in , then we get a⁰ = 1. That means, the graph of the f(x) always passes through the point (0, 1). As we seen below that the curve of the graph passes through the point (0, 1).

Property 2:

For any value of x, whether the x is positive or negative, the value of the function f(x) = a^x > 0. There is no x-intercept. It does not intersect the x-axis. In the above figure, the curve of the graph does not intersect anywhere on the x-axis.

Property 3:

The domain is the all real number. That means, the exponential function  is defined for all real values of x. Thus, from the above figure, we observe that the function is defined for all values of x.

Property 4:

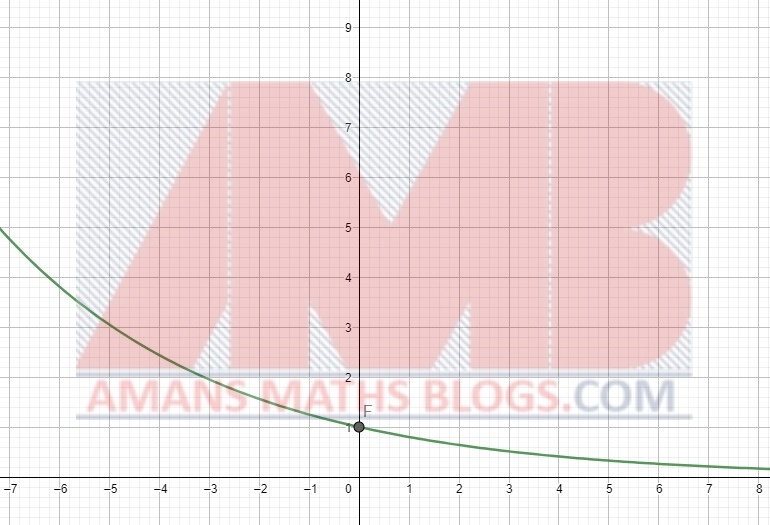
For 0 < a < 1, the graph of the function f(x) = a^x is decreasing as x → ∞.

Property 5:

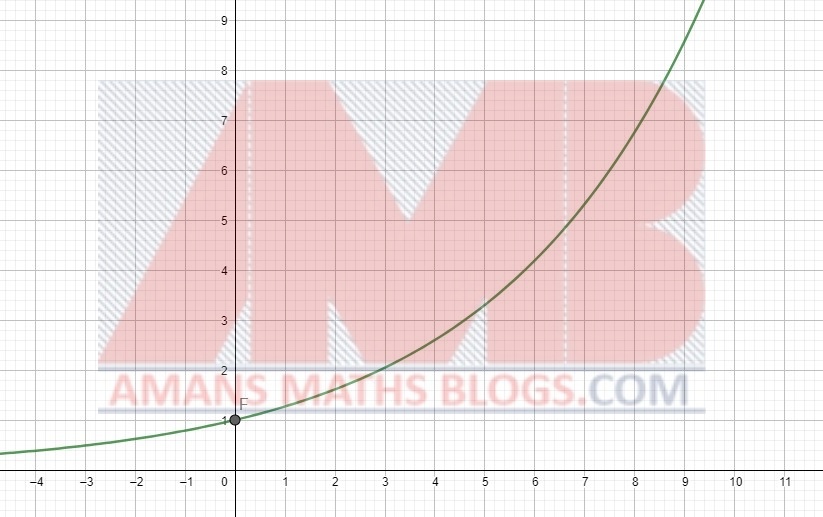
For a > 1, the graph of the function f(x) = a^x is increasing as x → ∞.

Property 6:

The function f(x) = a^x is an one-one function. If f(x) = f(y), then a^x = a^y. Hence, x = y. Thus, the exponential function f(x) = a^x is an one-one function.

Property 7:

The function f(x) = a^x is an on-to function. In the above graph, we observe that the co-domain of the function is equal to the range of the graph. Thus, the exponential function f(x) = a^x is an on-to function. 

To be an exponential function f(x) = a^x, it must follow all the properties from 1 to 7.

Please keep in mind that the properties no 4 and 5 is followed by the exponential function one at a time either the property no 4 or the property no 5.

If the exponential function follows the property no 4, then it does not follow the property no 5. Similarly, if the exponential function follows the property no 5, then it does not follow the property no 4.

Only one out of the properties no 4 or 5 must be followed by the exponential function. Not both the properties no 4 and 5 at a time. 

It means, the exponential function follows the six properties at a time out seven properties mentioned as above.

Now, the students I hope you understand all the above properties of the exponential function. So, lets go to clear all your doubts.

Doubt 1: The function f(x) = 0^x is NOT an exponential function.

Clarification: There are following reasons that the function f(x) = 0^x is not an exponential function.

Reason 1: Since 0⁰ is not defined, the function f(x) = 0^x is not defined at x = 0. Thus, this function does not pass through (0, 1). It violates the property no 1. Hence, it cannot be the exponential function. 

Reason 2: Since 0⁰ is not defined, the domain of the function f(x) = 0^x is R – {0}. Thus, it violates the property no 3. Hence, the function f(x) = 0^x is not an exponential function.

Reason 3: For base zero, a = 0  f(x) = 0^x. For any value of x, f(x) = 0. It is neither increasing function nor decreasing function. Then, it violates the properties no 4 and 5 of the exponential function as mentioned above. Hence, the function f(x) = 0^x is a not an exponential function. 

Reason 4: Since 0⁵ = 0⁶ = 0   5 ≠ 6, it is not an one-one function. It violates the property no 6. Thus, the function f(x) = 0^x is not an exponential function. 

Therefore, we can say that if a = 0 in the function f(x) = a^x, then it violates some of the properties of an exponential function and hence, f(x) = a^x = 0^x is not an exponential function.

Doubt 2: The function g(x) = 1^x is NOT an exponential function.

Clarification: There are following reasons that the function g(x) = 1^x is not an exponential function.

Reason 1: For any value of x, g(x) = 1. It is neither increasing function nor decreasing function. Then, it violates the properties no 4 or 5 of the exponential function as mentioned above. Hence, it is a constant function not an exponential function.

Reason 2: Since 1⁵ = 1⁶ = 1   5 ≠ 6, it is not an one-one function. It violates the property no 6. Thus, the function f(x) = 1^x is not an exponential function. 

Therefore, we can say that if a = 1 in the function g(x) = a^x, then it violates the some of the properties of an exponential function and hence g(x) = a^x = 1^x is not an exponential function for a = 1.

Doubt 3: The function h(x) = (-2)^x is NOT an exponential function.

Clarification: There are following reasons that the function h(x) = (-2)^x is not an exponential function.

Reason 1: For negative base, a = (–2)  h(x) = (–2)^x, 

At x = 0, the value of the function h(x) = (–2)^x is h(0) = (–2)⁰ = 1. 

At x = 1, the value of the function h(x) = (–2)^x is h(1) = (–2)¹ = –2. 

At x = 2, the value of the function h(x) = (–2)^x is h(2) = (–2)² = 4. 

At x = 3, the value of the function h(x) = (–2)^x is h(3) = (–2)³ = –8. 

At x = 4, the value of the function h(x) = (–2)^x is h(4) = (–2)⁴ = 16.

Here, we see that when the value of x increases the function h(x) = (–2)^x is neither increasing nor decreasing. it must be either increasing or decreasing when x is increases to become an exponential function. Thus, it violates the property no 4 or 5. Hence, the function h(x) = (–2)^x is not an exponential function. 

Therefore, the exponential function is defined as

Its domain is all real numbers, x ∈ (–∞, ∞) and its range is all positive real numbers, y ∈ (0, ∞). The functions f(x) = 0^x, g(x) = 1^x and h(x) = (–2)^x are not exponential functions. 

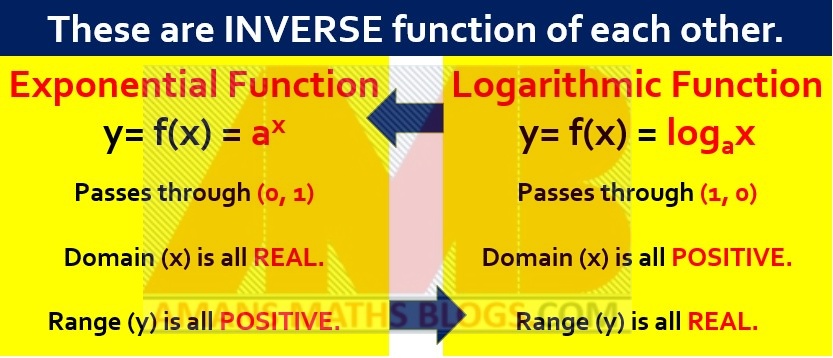
Since the function f(x) = a^x is an exponential function which is a one-one onto function, its inverse function exists. The inverse of the exponential function is known as the logarithmic function.

The inverse function graph is obtained by the creating image of the function graph with respect to x.

Now, the logarithmic function is defined as 

Now, the students I hope you understand the above definition of a logarithmic function. So, lets go to clear all your doubts.

Doubt 4: Why the base of logarithm cannot be negative, means a > 0?

Clarification: There is following reason that the base of the logarithm cannot be negative.

Reason: Since a > 0 in the exponential function f(x) = a^x, then its inverse function means logarithmic function f(x) = log_ax does not contain a < 0. The logarithmic function log_ax is defined for a > 0. That’s why the logarithmic function is not defined for negative base.

Doubt 5: Why the base of logarithm cannot be unity, means a ≠ 1?

Clarification: There is following reason that the base of the logarithmic cannot be one.

Reason: Now, we know that the exponential function f(x) = a^x is defined for a ≠ 1. Hence, its inverse function means logarithmic function f(x) = log_ax does not contain a = 1. The logarithmic function log_ax is defined for a ≠ 1. That’s why the logarithmic function is not defined for unity base.

Doubt 6: Why the logarithm of any negative number is not defined, mean log(-2) is not defined?

Clarification: There is following reason that the logarithm of any negative number is not defined.

Reason: In the exponential function y = f(x) = a^x, the range is all positive real numbers. That’s mean there is no value of x for which y is negative. Hence, its inverse function means logarithmic function f(x) = log_ax does not contain x < 0. The logarithmic function log_ax is defined for a positive number. That’s why the logarithmic function is not defined for negative number.

cbse maths solutionsexponent and powersexponentialexponential functionlogarithmiclogarithmic functionmaths blogncert maths solutionsncert solutions