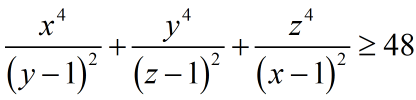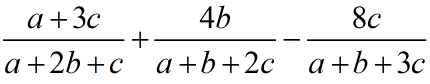Hi students, welcome to Amans Maths Blogs (AMB). Are you an aspirant of any competitive exams like CBSE Board, JEE, NTSE, NDA, NMTC etc.? If yes, then it is very important to solve the previous year questions papers to get the knowledge of the paper pattern of that particular examination. So, in this article, the students will get the NMTC final stage previous year question papers for class 9 and 10. These NMTC final stage previous year question papers are important for those students who qualify the NTSE Stage 1 exam.
Click Here NMTC 2019 Notification
Previous year question papers of NMTC helps the students in the following aspects:
(1) By solving previous year question papers of NMTC final stage previous year question papers for class 9 and 10, a students can identify the preparation level. What he studies or not completed their whole or not. So, the students must solve the NMCT previous year question papers.
(2) Most of the students are unaware the exams pattern of the NMTC final stage previous year question papers for class 9 and 10. So, if a student solves the NMTC previous year question papers, he will understand the exams pattern of NMTC.
(3) The question paper of the NMTC contains different sections like section A, section B or matrix match type true false etc question of NMTC final stage previous year question papers for class 9 and 10, the students must know the different level and the marking scheme of the exams.
(4)As we know that, there are a lot of questions in NMTC exams and all the questions are to be solved in a given time frame. Most of the students are well known concepts, syllabus, pattern and their difficulty level of MNTC. But how to solve those tricky questions in the given time frame. It will be learnt by solving previous year question papers of NMTC final stage previous year question papers for class 9 and 10.
(5) After completing the whole syllabus of NMTC, it is time to reverse all those concepts tips tricks etc. before appearing the exams of NMTC final stage previous year question papers for class 9 and 10. To revise all these concepts, the students must solve the previous year papers of NMTC. By solving the question papers of NMTC, a student quickly revises all his syllabus of NMTC.
(6) When a question paper is compiled for the NMTC in upcoming year, the question paper makes take a reference of its previous year question paper of NMTC. So, he may decide some question is to be same in upcoming year. Therefore, the students must solve the NMTC final stage previous year question papers for class 9 and 10. It may be possibility of a repeat question will be asked in upcoming year.
(7) If you want to feel the examination hall pressure on that day of NMTC exam, you need to solve the previous year question papers of NMTC and try to solve in given time duration of the papers. So, the students must try to solve the NMTC final stage previous year question papers for class 9 and 10 and feel the exam pressure.
Here, you can download the pdf of the previous year question papers of NMTC. This page provides the downloading links of the NMTC final stage previous year question papers for class 9 and 10.
NMTC Final Stage Previous Year 2014 Question Papers For Class 9 and 10
Instructions:
- Answer as many questions as possible.
- Elegant and novel solutions will be get extra credits.
- Diagram and explanations should be given wherever necessary.
- Fill in FACE SLIP and your rough working should be in the answer book.
- Maximum time allowed time is 3 hours.
- All questions carry equal marks.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 1
(a) p1, p2, p3, …, p2014 be an arbitrary rearrangement of 1, 2, 3, …, n. Show that 1/(p1 + p2) + 1/(p2 + p3) + … + 1/(p2013 + p2014) > 2013/2016.
(b) Find positive integers n such that
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 2
ABCD is a quadrilateral inscribed in a circle of centre O. Let BD bisects OC perpendicularly. P is a point on the diagonal AC such that PC = OC. BP cuts AD at E and the circle ABCD at F. Prove that PF is the geometric mean of EF and BF.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 3
(a) The Fibonacci sequence is defined by F0 = 1, F1 = 1, Fn = F(n–1) + F(n – 2) for natural numbers n ≥ 2. Show that 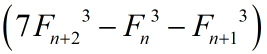
(b) If x, y, z are each greater than 1, show that
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 4
ABCD is a square E and F are points on BC and CD respectively such that AE cuts the diagonals BD at G and FG is perpendicular to AE. K is a point on FG such that AK = EF. Find the measure of the angle EKF.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 5
If none of a, b, c, x, y, z is zero and
then prove that a3 + b3 + c3 + abc = 0.
(b) Solve for x, y, z…. x/y + y/z + z/x = y/x + z/y + x/z = x + y + z = 3.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 6
In the dog language BOW, the alphabet consists of the letter B, O, W only. Independently of the choice of the BOW word of length n (i.e. number of letters is n) from which to start, one can construct all the BOW word with length n using iteratively the following rules.
(i) Invert the order of the letters of the word.
(ii) Replace two consecutive letters BO → WW, OW → BB, WB → OO, BB → OW or OO → WB. Given that BBOWOBOWWOBOWWWOBOWWWWOBB is a bow word, does the BOW language have the word.
(a) BWOBWOBWOBOWBOWBOWBOWBOWB
(b) OBWOBWOBWOBWOBWOBWOBWOBW?
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 7
A merchant bought a quantity of cotton; this he exchanged for oil which he sold. He observed that the number of kg of cotton, the number of litres of oil obtained for each kg and the number of rupees for which he sold formed a decreasing geometric progression. He calculated that if he had obtained 1 kg more of cotton, one litre more of oil for each kg and Re. 1 more for each litre, he would have obtained Rs. 10169 more, whereas if he had obtained one kg less of cotton and one litre of oil for each kg and Rs. 1 less for each litre, he would have obtained Rs. 9673 less. How much he actually received?
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 8
There are three towns A, B and C a person walking from A to B driving from B to C and riding from C to A makes the journey in 15(1/2) hours. By driving from A to B, riding from B to C and walking from C to A, he could make the journey in 12 hours. On foot he could make the journey in 22 hours, on horseback in 8(1/4) hours and driving in 11 hours. To walk 1 km, ride 1 km and drive 1 km, he takes altogether half an hour. Find the rates at which he travels and the distance between the towns.
NMTC Final Stage Previous Year 2015 Question Papers For Class 9 and 10
Instructions:
- Same as previous instructions.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 1
(a) 28 integers are chosen from the interval [104, 208]. Show that there exit two of them having a common prime divisor.
(b) AB is a line segment. C is a point on AB. ACPQ and CBRS are squares drawn on the same side AB. Prove the S is the orthocentre of the triangle APB.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 2
(a) a, b, c are distinct real numbers such that a3 = 3(b2 + c2) – 25, b3 = 3(c2 + a2) – 25, c3 = 3(c2 + b2) – 25. Find the numerical value of abc.
(b) a = 1 + 1/22 + 1/32 + 1/42 + … + 1/20152. Find [a], where [a] denotes the integer part of a.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 3
The arithmetic mean of a number of pair wise distinct numbers is 27. Determine the biggest prime among them.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 4
65 bugs are replaced at different squares of a 9 × 9 square board. A bug in each moves to a horizontal or vertical adjacent square. No bug makes two horizontal or two vertical moves in succession. Show that after some moves, there will be at least two bugs in the same square.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 5
f(x) is a fifth degree polynomial. It is given that f(x) + 1 in divisible by (x – 1)3 and f(x) – 1 is divisible by (x + 1)3. Find f(x).
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 6
ABC and DBC are two equilateral triangles on the same base BC, A point P is taken on the circle with centre D, radius BD. Show that PA, PB, PC are the side of a right triangle.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 7
a, b, c are real numbers such that a + b + c = 0 and a2 + b2 + c2 = 1. Prove that a2b2c2 ≤ 1/54. When does the equality hold?
NMTC Final Stage Previous Year 2016 Question Papers For Class 9 and 10
Instructions:
- Same as previous instructions.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 1
(a) If a, b, c are positive reals and a + b + c = 50 and 3a + b – c = 70. If x = 5a + 4b + 2c, find the range of values of x.
(b) The sides a, b, c of a triangle ABC satisfy the equation a2 + 2b2 + 2016c2 – 3ab – 4033bc + 2017ac = 0. Prove that b is the arithmetic mean a, c.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 2
In an isosceles triangle ABC, AB = AC. The bisector AD of ∠ A meets the side BC at D. The line perpendicular to AD through D meets AB at F and AC produced at E. Perpendiculars from B and D to AC are respectively BM and DN. If AE = 2016 units, find the length MN.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 3
(a) Two circles with centres at P and Q and radii and 1 respectively intersect each other at A and D and PQ = 2 units. Chord AC is drawn to the bigger circle to cut it at C and the smaller circle at B such that B is the midpoint of AC. Find the length of AC.
(b) Find the greatest common divisor of the numbers n2 – n, n = 3, 5, 7, 9, …
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 4
(a) A book contained problems an Algebra, Geometry and Number Theory. Mahadeven solved some of them. After checking the answers, he found that he answered correctly 50% problems in Algebra, 70% in Geometry and 80% in Number Theory. He further found that he solved 62% of problems in Algebra and Number Theory put together, 74% questions in Geometry and Number Theory altogether. What is the percentage of correctly answered questions in all the three subjects?
(b) Find all the pairs of positive integers (a, b) such that ab – ba = 3.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 5
a, b, c are positive real numbers. Find the minimum value of
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 6
(a) Show that among any (n + 1) whole numbers, one can find the two numbers such that their difference is divisible by n.
(b) Show that for any natural number n, there is a positive integer all of whose digits are 5 or 0 and is divisible by n.
NMTC Final Stage Previous Year 2017 Question Papers For Class 9 and 10
Instructions:
- Same as previous instructions.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 1
(a) Find all the prime numbers p such that 4p2 + 1 and 6p2 + 1 are also primes.
(b) Determine real numbers x, y, z, u such that
xyz + xy + yz + zx + x + y + z = 7,
yzu + yz + zu + uy + y + z + u = 9,
zux + zu + ux + xz + z + u + x = 9,
uxy + ux + xy + yu + u + x + y = 9.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 2
If x, y, z, p, q, r are distinct real numbers such that
1/(x + p) + 1/(y + p) + 1/(z + p) = 1/p,
1/(x + q) + 1/(y + q) + 1/(z + q) = 1/q,
1/(x + r) + 1/(y + r) + 1/(z + r) = 1/r,
Find the numerical value of (1/p + 1/q + 1/r).
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 3
ADC and ABC are triangles such that AD = DC and CA = AB. If ∠ CAB = 20° and ∠ ACD = 100°, without using trigonometry, prove that AB = BC + CD.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 4
(a) a, b, c, d are positive real numbers such that abcd = 1. Prove that (1 + ab)/(1 + a) + (1 + bc)/(1 + b) + (1 + cd)/(1 + c) + (1 + ad)/(1 + d) ≥ 4.
(b) In a scalene triangle ABC, ∠ BAC = 120°. The bisectors of the angle A, B and C meet the opposite sides in P, Q and R respectively. Prove that the circle on QR as diameter passes through the point P.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 5
(a) Prove that x4 + 3x3 + 6x2 + 9x + 12 cannot be expressed as a product of two polynomials of degree 2 with integer coefficients.
(b) (2n + 1) segments are marked on a line. Each of these segments intersects at least n other segments. Prove that one of these segments intersects all other segments.
NMTC Final Stage Previous Year Question For Class 9 and 10: Ques No 6
If a, b, c, d are positive real numbers such that a2 + b2 = c2 + d2 and a2 + d2 – ad = b2 + c2 + bc, find the value of (ab + cd)/(ad + bc).