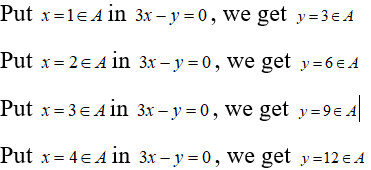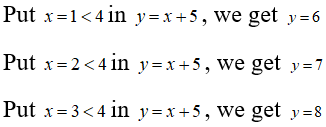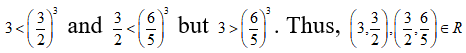NCERT Solutions for Class 12 Maths Relations and Functions

Hi Students, Welcome to Amans Maths Blogs (AMB). In this post, you will get the NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1. This NCERT Solutions can be downloaded in PDF file. The downloading link is given at last.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 1. 

Determine whether each of the following relations are reflexive, symmetric and transitive:
(i) Relation R in the set A = {1, 2, 3, …, 13, 14} defined as R = {(x, y) : 3x – y = 0}
NCERT Solutions:
Given that the Relation R in the set A = {1, 2, 3, …, 13, 14} defined as
R = {(x, y) : 3x – y = 0}

Thus, R = {(1, 3), (2, 6), (3, 9), (4, 12)}

Since, thus the given relation R is not reflexive.

Since,  thus the given relation R is not symmetric.

Since, thus the given relation R is not transitive.

(ii) Relation R in the set N of natural numbers defined as R = {(x, y) : y = x + 5 and x < 4}
NCERT Solutions:
Given that the Relation R in the set N of natural numbers defined as R = {(x, y) : y = x + 5 and x < 4}

Thus, R = {(1, 6), (2, 7), (3, 8)}

Since , thus the given relation R is not reflexive.

Since , thus the given relation R is not symmetric.

Since there is no pair in R such that (x, y) and (y, x) belong R such that (x, z) cannot belong R, thus the given relation R is not transitive.

Thus, the given relation is neither reflexive nor symmetric nor transitive.

(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x, y): y is divisible by x}
NCERT Solutions:
Given that the Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x, y) : y is divisible by x}
Since

1 is divisible by 1, means (1, 1)
2 is divisible by 2 and 1, means (2, 2), (1, 2)
3 is divisible by 3 and 1, means (3, 3), (1, 3)
4 is divisible by 4, 2 and 1, means (4, 4), (2, 4), (1, 4)
5 is divisible by 5 and 1, means (5, 5), (1, 5)
6 is divisible by 6, 3, 2 and 1, means (6, 6), (3, 6), (2, 6), (1, 6).

Then,

Thus, the given relation is reflexive and transitive but not symmetric.

(iv) Relation R in the set Z of all integers defined as R = {(x, y) : x – y is an integer}
NCERT Solutions:
Given that the Relation R in Z of all integers defined as R = {(x, y) : x – y is an integer}

Since for every ,  as x – x = 0 which is an integer, then R is reflexive.

Since for every ,  then x – y and y – x is also an integer, then  is symmetric.

Let (x – y) is an integer and (y – z) is an integer, then (x – z) is also an integer.
thus  and , hence R is transitive.

Thus, the given relation is reflexive, symmetric and transitive.

(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y) : x and y work at the same place}
NCERT Solutions:
Given that the Relation R in the set A of human beings in a town at a particular time given by R = {(x, y) : x and y work at the same place}

Since x and x work at the same place, then . Hence, R is reflexive.

Let x and y work at the same place. Then, y and x work at the same place, so . Hence, R is symmetric.

Let x and y work at the same place and also y and z work at the same place. Then, x and z work at the same place so . Hence, R is transitive.

Thus, the given relation is reflexive, symmetric and transitive.

(b) R = {(x, y) : x and y live in the same locality}
NCERT Solutions:
Given that the Relation R in the set A of human beings in a town at a particular time given by R = {(x, y) : x and y live in the same locality}

Since x and x live in the same locality, then . Hence, R is reflexive.

Let x and y live in the same locality. Then, y and x live in the same locality, so   . Hence, R is symmetric.

Let x and y live in the same locality and also y and z live in the same locality. Then, x and z live in the same locality so . Hence, R is transitive.

Thus, the given relation is reflexive, symmetric and transitive.

(c) R = {(x, y) : x is exactly 7 cm taller than y}
NCERT Solutions:
Given that the Relation R in the set A of human beings in a town at a particular time given by R = {(x, y) : x is exactly 7 cm taller than y}

Since x cannot be taller than x (himself), then. Hence, R is not reflexive.

Let x is exactly 7 cm taller than y. Then, y is not taller than x, so but . Hence, R is not symmetric.

Let x is exactly 7 cm taller than y and also y is exactly 7 cm taller than z. Then, x is exactly 14 cm taller than y so . Hence, R is not transitive.

Thus, the given relation is neither reflexive nor symmetric nor transitive.

(d) R = {(x, y) : x is wife of y}
NCERT Solutions:
Given that the Relation R in the set A of human beings in a town at a particular time given by R = {(x, y) : x is wife of y}

Since x cannot be the wife of x (himself), then . Hence, R is not reflexive.

Let x is wife of y. Then, y is not wife of x, so  but  . Hence, R is not symmetric.

Let x is wife of y. Then, y is not a wife of z and hence x is not a wife of z so . Hence, R is not transitive.

Thus, the given relation is neither reflexive nor symmetric nor transitive.

(e) R = {(x, y) : x is father of y}

NCERT Solutions:
Given that the Relation R in the set A of human beings in a town at a particular time given by R = {(x, y) : x is father of y}

Since x cannot be the father of x (himself), then . Hence, R is not reflexive.

Let x is father of y. Then, x cannot be the father of y, so  but   . Hence, R is not symmetric.

Let x is father of y and y is father of z. Then, x is not father of z so  . Hence, R is not transitive.

Thus, the given relation is neither reflexive nor symmetric nor transitive.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 2. 

Show that the relation R in the set R of real numbers, defined as R = {(a, b) : a ≤ } is neither reflexive nor symmetric nor transitive.
NCERT Solutions:
Let a real number is . then is not true. Thus, .Hence, R is not reflexive.

Let a = 1 and b = 5, then 1 < 25 but 5 is not less than 1. Thus . Hence, R is not symmetric.

Now, then 3 < 4 and 2 < 2.89 but 3 > 2.89. Thus, but . Hence, R is not transitive.

Thus, the given relation is neither reflexive nor symmetric nor transitive.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 3.

Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive.
NCERT Solutions:
Let A = {1, 2, 3, 4, 5, 6} and given that R = {(a, b) : b = a + 1}. Then, R = {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}

Since , thus the given relation R is not symmetric.

Since , thus the given relation R is not symmetric.

Since , thus the given relation R is not transitive.

Thus, the given relation is neither reflexive nor symmetric nor transitive.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 4.

Show that the relation R in R defined as R = {(a, b) : a ≤ b}, is reflexive and transitive but not symmetric.
NCERT Solutions:
Given that R = {(a, b) : a ≤ b}. 

Since every number is equal to itself (a = a), then . Thus, the given relation R is reflexive.

Let a = 1 and b = 4. Since 1 < 4 but 4 >1, then Thus, the given relation R is not symmetric.

Now, let a < b and b < c. Then, a < c. Thus, Hence, the given relation R is transitive. 

Thus, the given relation R is reflexive and transitive but not symmetric.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 5. 

Check whether the relation R in Real defined by R = {(a, b) : a ≤ b³} is reflexive, symmetric or transitive.
NCERT Solutions:
Given that R = {(a, b) : a ≤ }.

Let a real number is , then is not true. Thus, . Hence, R is not reflexive.

Let a = 1 and b = 5, then 1 < 125 but 125 is not less than 1. Thus,  but . Hence, R is not symmetric.

Now 

Hence, R is not transitive.

Thus, the given relation is neither reflexive nor symmetric nor transitive.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 6. 

Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
NCERT Solutions:
Given that A = {1, 2, 3} and R = {(1, 2), (2, 1)}

Since (1, 1) is not in R, thus the given relation R is not reflexive.

Since , thus the given relation R is symmetric.

Since but (1, 1) is not in R, thus the given relation R is not transitive.

Thus, the given relation is neither reflexive nor symmetric nor transitive.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 7. 

Show that the relation R in the set A of all the books in a library of a college, given by R = {(x, y) : x and y have same number of pages} is an equivalence relation.

NCERT Solutions:

Given that Set A is the set of all books in the library of a college and R = {x, y): x and y have the same number of pages}.

Since x and x has the same number of pages, then (x, x) ∈ R. Thus, the given relation R is reflexive.

Now, let x and y have the same number of pages, then y and x also have the same number of pages. Thus, (x, y) ∈ R and (y, x) ∈ R. Hence, the given relation R is symmetric.

Now, let x and y and have the same number of pages and y and z have the same number of pages. Then x and z have the same number of pages. Thus, (x, y), (y, z) ∈ R and (x, z) ∈ R. Hence, the given relation R is transitive.

Thus, the given relation is equivalence relation.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 8. 

Show that the relation R in the set A = {1, 2, 3, 4, 5} given by ? = {(?, ?): |? − ?| ?? ????}, is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2, 4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.

NCERT Solutions:

Given that A = {1, 2, 3, 4, 5} and R = {(a, b): |a-b| is even}.

Since for any element a ∈ A, we have |a – a| = 0 (which is even). Thus, (a, a) ∈ R. Thus, the given relation R is reflexive.

Now, Let (a, b) ∈ R. Then, |? − ?| ?? ???? ⇒|–(a –b)|= |b – a| is also even ⇒ (b, a) ∈ R. Thus, the given relation R is symmetric.

Now, let (a, b) ∈ R and (b, c) ∈ R such that |a-b| is even and |b – c| is even. So, (a-b) is even and (b-c) is even (a – c) = (a – b) + (b – c) is even. |? − ?| ?? ????. Thus, (a, c) ∈ R. Hence, the given relation R is transitive.

Thus, the given relation is equivalence relation.

Since all elements of the set {1, 3, 5} are related to each other and the elements of this subset are odd. Thus, |1 – 3|, |3 – 1|, |5 –1|, |1 – 5|, |3 – 5|, |5 – 3| are even.

Similarly, all elements of the set {2, 4} are related to each other as all the elements of this subset are even. Thus, |2 – 4|, |4 – 2| are even.

But, |1 – 2|, |2 – 1|, |1 –4|, |4 – 1|, |3 – 2|, |2 – 3|, |5 – 2|, |2 – 5| all are odd. Thus, no element of {1, 3, 5} is related to any element of {2, 4}.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 9. 

Show that each of the relation R in the set A = {x ∈ Z: 0 ≤ x ≤ 12}, given by (i) R = {(a, b): |a – b| is a multiple of 4} (ii) R = {(a, b): a = b} is an equivalence relation. Find the set of all elements related to 1 in each case.

NCERT Solutions:

(i)

Given that set ? = {? ∈ ?: 0 ≤ ? ≤ 12} {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.

Since for any element a ∈ A, we have |a – a| = 0 (which is multiple of 4). Thus, (a, a) ∈ R. Thus, the given relation R is reflexive.

Now, let (a, b) ∈ R and |a – b| is a multiple of 4. Thus, |– (b – a)| = |b – a| is a multiple of 4. Therefore, (b, a) ∈ R. Thus, the given relation R is symmetric.

Now, let (a, b), (b, c) ∈ R such that |a – b| is a multiple of 4 and |b – c| is a multiple of 4. Thus, (a – b) is a multiple of 4 and (b – c) is a multiple of 4. (a – c) = (a – b) + (b – c) is a multiple of 4. |a – c| is a multiple of 4. Hence, the given relation R is transitive.

Thus, the given relation is equivalence relation.

The set of elements related to 1 is {1, 5, 9} as |1 – 1|, |5 – 1|, |9 – 1| is a multiple of 4.

(ii)

Given that set ? = {? ∈ ?: 0 ≤ ? ≤ 12} {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.

Since for any element a ∈ A, we have a = a. Thus, (a, a) ∈ R. Thus, the given relation R is reflexive.

Now, let (a, b) ∈ R and a = b and b = a. Therefore, (b, a) ∈ R. Thus, the given relation R is symmetric.

Now, let (a, b), (b, c) ∈ R such that a = b and b = c. Thus, a = c. So, (a, c) ∈ R. Hence, the given relation R is transitive.

Thus, the given relation is equivalence relation.

Since 1 = 1, the elements in R that are related to 1 will be those elements from set A which are equal to 1. Hence, the set of elements related to 1 is {1}.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 10. 

Give an example of a relation. Which is

(i) Symmetric but neither reflexive nor transitive.

NCERT Solutions:

Let A = {5, 6, 7}. Define a relation R on A as R = {(5, 6), (6, 5)}.

Relation R is not reflexive as (5, 5), (6, 6), (7, 7) ∉ R. Now, as (5, 6) ∈ R and also (6, 5) ∈ R, R is symmetric.

Since (5, 6), (6, 5) ∈ R, but (5, 5) ∉ R. Thus, R is not transitive.

Hence, relation R is symmetric but not reflexive or transitive.

(ii) Transitive but neither reflexive nor symmetric.

NCERT Solutions:

Let R = {(a, c): a < c}.

Since for any a ∈ R, a cannot be strictly less than a itself, we have (a, a) ∉ R. Thus, the relation R is not reflexive.

Now, (1, 3) ∈ R (as 1 < 3) but 2 is not less than 1. Thus, (2, 1) ∉ R. Therefore, R is not symmetric.

Now, let (a, b), (b, c) ∈ R such that a < b and b < c. Thus, a < c so (a, c) ∈ R. Hence, R is transitive.

Hence, relation R is transitive but not reflexive and symmetric.

(iii) Reflexive and symmetric but not transitive.

NCERT Solutions:

Let A = {4, 6, 8} and a relation R on A as

A = {(4, 4), (6, 6), (8, 8), (4, 6), (6, 4), (6, 8), (8, 6)}.

Since {(4, 4), (6, 6), (8, 8)} ∈ R, Thus, the relation R is not reflexive.

Since (4, 6) ∈ R and (6, 4) ∈ R, (6, 8) ∈ R and (8, 6) ∈ R therefore, R is symmetric.

Since (4, 6), (6, 8) ∈ R but (4, 8) ∉ R, then R is not transitive.

Hence, relation R is reflexive and symmetric but not transitive.

(iv) Reflexive and transitive but not symmetric.

NCERT Solutions:

Let a relation R in R as 

Since, then (a, a) ∈ R. Thus, the relation is reflexive.

Now let (2, 1) ∈ R such that . But, (1, 2) ∉ R. Thus, R is not symmetric.

Now let (a, b), (b, c) ∈ R such that. Then,. Thus, (a, c) ∈ R. Thus, the relation R is transitive.

Hence, the relation R is reflexive and transitive but not symmetric.

(v) Symmetric and transitive but not reflexive.

NCERT Solutions:

Let A = {–5, –6} and a relation R on A as R = {(−5, −6), (−6, −5), (−5, −5)}

Since (−6, −6) ∉ R, Thus, the relation R is not reflexive.

Since (−5, −6) ∈ R and (−6, −5) ∈ R, then the relation R is symmetric.

Since (−5, −6), (−6, −5) ∈ R and (–5, –5) ∈ R, then the relation R is transitive.

Hence, relation R is symmetric and transitive but not reflexive.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 11. 

Show that the relation R in the set A of points in a plane given by R = {(P, Q) : distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all points related to a point P ≠ (0, 0) is the circle passing through P with origin as center.

NCERT Solutions:

Given that R = {(P, Q): Distance of point P from the origin is the same as the distance of point Q from the origin}

Let (P, P) ∈ R.  since the distance of point P from the origin is always the same as the distance of the same point P from the origin. Thus, the given relation R is reflexive.

Now, Let (P, Q) ∈ R. It means, the distance of point P from the origin is the same as the distance of point Q from the origin. In other words, we can also say that the distance of point Q from the origin is the same as the distance of point P from the origin. Then, (Q, P) ∈ R. Thus, the given relation R is symmetric.

Now, Let (P, Q), (Q, S) ∈ R. It means, the distance of points P and Q from the origin is the same and also, the distance of points Q and S from the origin is the same. Thus, the distance of points P and S from the origin is the same. So, (P, S) ∈ R. Hence, the given relation R is transitive.

Therefore, R is an equivalence relation.

If O (0, 0) is the origin and the set of all points related to P ≠ (0, 0) such that OP = k, then the set of all points related to P is at a distance of k from the origin. Thus, this set of points forms a circle with the center as the origin and this circle passes through point P.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 12. 

Show that the relation R defined in the set A of all triangles as R = {(T1, T2) : T1 is similar to T2}, is equivalence relation. Consider three right angle triangles T1 with sides 3, 4, 5, T2 with sides 5, 12, 13 and T3 with sides 6, 8, 10. Which triangles among T1, T2 and T3 are related?

NCERT Solutions:

Given that R = {(T1, T2): T1 is similar to T2}.

Since every triangle is similar to itself. Then, (T1, T2) ∈ R. Thus, the given relation R is reflexive.

Let (T1, T2) ∈ R. Then, T1 is similar to T2 or T2 is similar to T1. Thus, (T2, T1) ∈ R. Hence, the given relation R is symmetric.

Now, let (T1, T2), (T2, T3) ∈ R. Then, T1 is similar to T2 and T2 is similar to T3. Thus, T1 is similar to T3. So, (T1, T3) ∈ R. Thus, the given relation R is transitive.

Therefore, R is an equivalence relation.

Now, in triangles T1 and T3, we have . Thus, the triangles T1 and T3 are similar. Hence, T1 and T3 are related by given relation R.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 13. 

Show that the relation R defined in the set A of all polygons as R = {(P₁ , P₂): P₁ and P₂ have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3, 4 and 5?

NCERT Solutions:

Given that R = {(P₁, P₂): P₁ and P₂ have same number of sides}.

Since every polygon has the same number of sides with itself. Then, (P₁, P₁) ∈ R. Thus, the given relation R is reflexive.

Let (P₁, P₂) ∈ R. Then, P₁ has same number of sides as the polygon P₂ or P₂ has same number of sides as the polygon P₁. Thus, (P₂, P₁) ∈ R. Hence, the given relation R is symmetric.

Now, let (P₁, P₂), (P₂, P₃) ∈ R. Then, P₁ has same number of sides as the polygon P₂ and P₂ has same number of sides as the polygon P₃. Thus, P₁ has same number of sides as the polygon P₃. So, (P₁, P₃) ∈ R. Thus, the given relation R is transitive.

Therefore, R is an equivalence relation.

The elements in A related to the right-angled triangle (T) with sides 3, 4, and 5 are those polygons which have 3 sides (Since T is a polygon with 3 sides). Hence, the set of all elements in A related to triangle T is the set of all triangles.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 14. 

Let L be the set of all lines in XY plane and R be the relation in L defined as R = {(L₁, L₂) : L₁ is parallel to L₂}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.

NCERT Solutions:

Given that R = {(L₁, L₂): L₁ is parallel to L₂}.

Since every line is parallel with itself, then (L₁, L₁) ∈ R. Thus, the given relation R is reflexive.

Let (L₁, L₂) ∈ R. Then, L₁ is parallel to L₂ or L₂ is parallel to L₁. Thus, (L₂, L₁) ∈ R. Hence, the given relation R is symmetric.

Now, let (L₁, L₂), (L₂, L₃) ∈ R. Then, L₁ is parallel to L₂ and L₂ is parallel to L₃. Thus, L₁ is parallel to L₃. So, (L₁, L₃) ∈ R. Thus, the given relation R is transitive.

Therefore, R is an equivalence relation.

Now, in the line y = 2x + 4. The slope of the line is m = 2. Since the slope of the parallel lines are same. Thus, the set of all lines related to the line y = 2x + 4 is y = 2x + c, where c is any real number.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 15. 

Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4,4), (1, 3), (3, 3), (3, 2)}. Choose the correct answer.

(A) R is reflexive and symmetric but not transitive.

(B) R is reflexive and transitive but not symmetric.

(C) R is symmetric and transitive but not reflexive.

(D) R is an equivalence relation.

NCERT Solutions:

Correct Answer is B.

Given that R = {(1, 2), (2, 2), (1, 1), (4,4), (1, 3), (3, 3), (3, 2)}.

Since (1, 1), (2, 2), (3, 3), (4, 4) ∈ R, then the given relation R is reflexive.

Since (1, 2) ∈ R but (2, 1) ∉ R then the given relation R is not symmetric.

Since (1, 3), (3, 2) ∈ R and (1, 2) ∈ R then the given relation R is transitive.

Thus, the given relation R is reflexive and transitive but not symmetric. Option B is correct.

NCERT Solutions for Class 12 Maths Relations and Functions Exercise 1.1: Ques No 16. 

Let R be the relation in the set N given by R = {(a, b) : a = b – 2, b > 6}. Choose the correct answer.

(A) (2, 4) ∈ R        (B) (3, 8) ∈ R        (C) (6, 8) ∈ R        (D) (8, 7) ∈ R

NCERT Solutions:

Given that R = {(a, b): a = b − 2, b > 6}

In option C, b = 8 > 6

Put b = 8 in a = b – 2.  We get a = 6.

Thus, (6, 8) ∈ R

In option D, b = 7 > 6

Put b = 7 in a = b – 2.  We get a = 5.

Thus, (8, 7) ∉ R.

Therefore, the correct answer is C.

class 12 maths ncert solutionsncert solutionsncert solutions class 12ncert solutions class 12 mathsncert solutions class 12th mathsncert solutions class 12th maths pdfncert solutions for class 12ncert solutions for class 12 mathsrelations and functionsrelations and functions class 12relations and functions class 12 ncert solutions