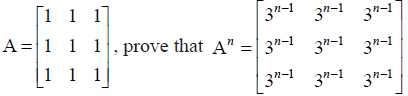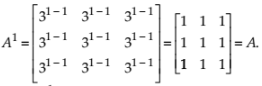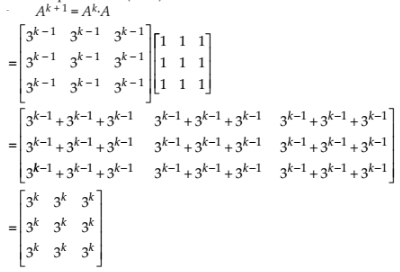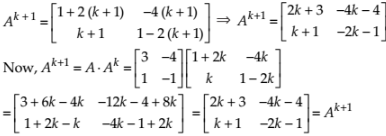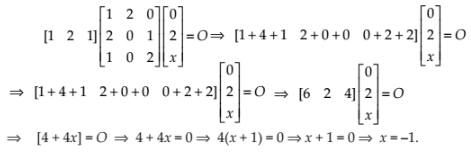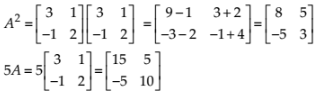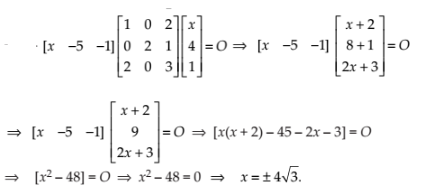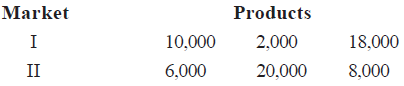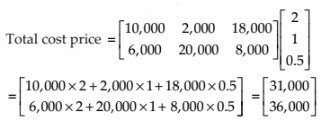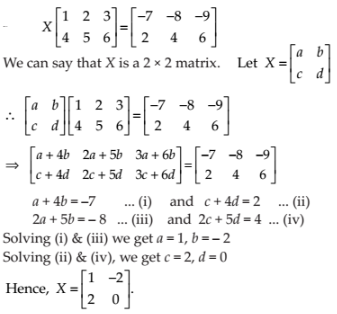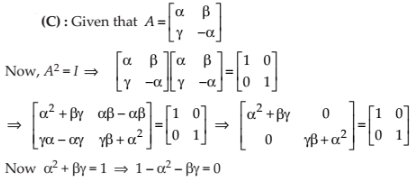NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise

Hi Students, Welcome to Amans Maths Blogs (AMB). In this post, you will get the NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise. This NCERT Solutions can be downloaded in PDF file. The downloading link is given at last.

NCERT Solutions for Class 12 Maths are not only the solutions of Maths exercise but it builds your foundation of other important subjects. Getting knowledge of depth concept of CBSE Class 12^th Maths like Algebra, Calculus, Trigonometry, Coordinate Geometry help you to understand the concept of Physics and Physical Chemistry.

CBSE Class 12^th is an important school class in your life as you take some serious decision about your career. And out of all subjects, Maths is an important and core subjects. So CBSE NCERT Solutions for Class 12^th Maths is major role in your exam preparation as it has detailed chapter wise solutions for all exercise.

As we know that all the schools affiliated from CBSE follow the NCERT books for all subjects. You can check the CBSE NCERT Syllabus. Thus, NCERT Solutions helps the students to solve the exercise questions as given in NCERT Books.

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 1.

Let 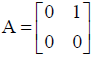, show that (aI + bA)ⁿ = aⁿI + na^{n – 1}bA, where I is the identity matrix of order 2 and n ∈ N.

NCERT Solutions:

To prove this, we use mathematical induction.

Given that p(n) : (aI + bA)ⁿ = aⁿI + na^{n – 1}bA.

At n = 1, we have p(1) : (aI + bA)¹ = a¹I + 1a^{1 – 1}bA = al + bA

Now, at n = k, we let p(k) : (aI + bA)^k = a^kI + ka^{k – 1}bA is true, …… (1)

Thus, we need to prove that at n = k + 1, p(k + 1) : (aI + bA)^{k + 1} = a^{k + 1}I + (k + 1)a^{k + 1 – 1}bA.

LHS = (aI + bA)^{k + 1}

= (aI + bA)^k(aI + bA)

= (a^kI + ka^{k – 1}bA)(aI + bA)                           (From (1))

= a^{k + 1}I x I + ka^kbAI + a^kbAI + ka^{k – 1}b²A²

= a^{k + 1}I + ka^kbA + a^kbA + ka^{k – 1}b² x 0      (A² = 0)

= a^{k + 1}I + (k + 1)a^{(k + 1) – 1}bA = RHS.

Hence, p(n) : (aI + bA)ⁿ = aⁿI + na^{n – 1}bA; it is also true at n = k + 1.

Therefore, p(n) : (aI + bA)ⁿ = aⁿI + na^{n – 1}bA is true for all values of n ∈ N.

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 2.

If

NCERT Solutions:

To prove this, we use mathematical induction.

Given that p(n) : .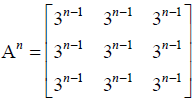

At n = 1, we have p(1) :

Now, at n = k, we let p(k) : 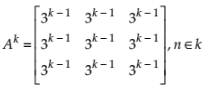is true, …… (1)

Thus, we need to prove that at n = k + 1.

Therefore, by principle of mathematical induction, we get that .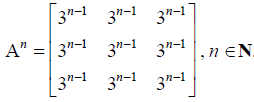

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 3.

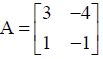
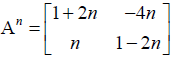
If , then , prove that A where n is any positive integer.

NCERT Solutions:

To prove this, we use mathematical induction.

Given that p(n) : .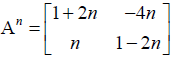

At n = 1, we have p(1) : .

Now, at n = k, we let p(k) : is true, …… (1)

Thus, we need to prove that at n = k + 1.

Therefore, by principle of mathematical induction, we get that 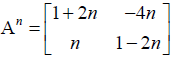for any positive integer n.

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 4.

If A and B are symmetric matrices, prove that AB – BA is a skew symmetric matrix.

NCERT Solutions:

Since A and B are symmetric matrices, A’ = A and B’ = B. To prove that (AB – BA) is skew symmetric matrix. It means, we need to prove (AB – BA)’ = -(AB – BA).

Now, LHS = (AB – BA)’ = (AB)’ – (BA)’ = B’A’ – A’B’ = BA – AB = -(AB – BA) = RHS.

Hence, (AB – BA) is skew symmetric matrix.

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 5.

Show that the matrix B′AB is symmetric or skew symmetric according as A is symmetric or skew symmetric.

NCERT Solutions:

Case I: Given that A is symmetric It means, A’ = A.

We need to prove that B’AB is symmetric. It means, we need to prove (B’AB)’ = B’AB.

LHS = (B’AB)’ = B’A'(B’)’ = B’A’B = B’AB = RHS.

Hence, B’AB is symmetric.

Case II: Given that A is skew-symmetric It means, A’ = -A.

We need to prove that B’AB is skew-symmetric. It means, we need to prove (B’AB)’ = -B’AB.

LHS = (B’AB)’ = B’A'(B’)’ = B’A’B = B'(-A)B = -B’AB = RHS.

Hence, B’AB is skew-symmetric.

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 6.

Find the values of x, y, z if the matrix 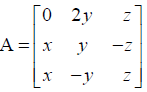satisfy the equation A′A = I.

NCERT Solutions:

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 7.

For what values of x : ?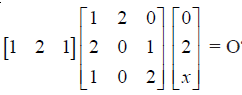

NCERT Solutions:

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 8.

If 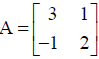 , show that A² – 5A + 7I = 0.

NCERT Solutions:

Given that .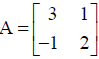

Now, 

Put these values in A² – 5A + 7I, we get 

LHS = = RHS

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 9.

Find x, if .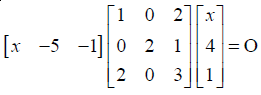

NCERT Solutions:

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 10.

A manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below.

(a) If unit sale prices of x, y and z are Rs 2.50, Rs 1.50 and Rs 1.00, respectively, find the total revenue in each market with the help of matrix algebra.

NCERT Solutions:

Let quantity matrix is .

And, unit selling price matrix is .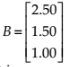

Now, total selling price matrix is

Thus, total revenue in Market 1 is Rs. 46000 and in Market 2 is Rs. 53000.

(b) If the unit costs of the above three commodities are Rs 2.00, Rs 1.00 and 50 paise respectively. Find the gross profit.

NCERT Solutions:

Let quantity matrix is .

Now, cost price matrix is

Thus,

Total cost price, CP = 31000 + 36000 = Rs. 67000.

Total selling price, SP = 46000 + 53000 = Rs. 99000.

Profit = SP – CP = 99000 – 67000 = Rs. 32000.

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 11.

A manufacturer produces three products x, y, z which he sells in two markets. Annual sales are indicated below.

NCERT Solutions:

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 12.

If A and B are square matrices of the same order such that AB = BA, then prove by induction that ABⁿ = BⁿA. Further, prove that (AB)ⁿ = AⁿBⁿ for all n ∈ N.

NCERT Solutions:

To prove this, we use mathematical induction.

Given that p(n) : ABⁿ = BⁿA.

At n = 1, we have p(1) : AB = BA.

Now, at n = k, we let p(k) : AB^k = B^kA is true, …… (1)

Thus, we need to prove that at n = k + 1, p(k + 1) : AB^{k + 1} = B^{k + 1}A.

LHS = AB^{k + 1} = AB^kB = (AB)B^k = (BA)B^k = B^k+1A = RHS

Hence, p(n) : ABⁿ = BⁿA; it is also true at n = k + 1.

Therefore, p(n) : ABⁿ = BⁿA is true for all values of n ∈ N.

Now, Again given that p(n) : (AB)ⁿ = AⁿBⁿ.

At n = 1, we have p(1) : AB = BA.

Now, at n = k, we let p(k) : (AB)^k = A^kB^k is true, …… (1)

Thus, we need to prove that at n = k + 1, p(k + 1) : (AB)^k+1 = A^k+1B^k+1.

LHS = (AB)^{k + 1} = (AB)^k(AB) = A^k(B^kB)A = A^k(B^k+1)A = A^k(AB^k+1) = A^k+1B^k+1 = RHS.

Hence, p(n) : (AB)ⁿ = AⁿBⁿ; it is also true at n = k + 1.

Therefore, p(n) : (AB)ⁿ = AⁿBⁿ is true for all values of n ∈ N.

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 13.

If 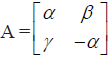 is such that A² = I, then

(A) 1 + α² + βγ = 0

(B) 1 – α² + βγ = 0

(C) 1 – α² – βγ = 0

(D) 1 + α² – βγ = 0

NCERT Solutions:

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 14.

If the matrix A is both symmetric and skew symmetric, then

(A) A is a diagonal matrix

(B) A is a zero matrix

(C) A is a square matrix

(D) None of these

NCERT Solutions:

B.

Since A is symmetric and skew-symmetric both, we have A’ = A and A’ = -A.

Then, A = -A ⟹ 2A = 0 ⟹ A = 0 ⟹ A is a zero matrix.

NCERT Solutions for Class 12 Maths Matrices Miscellaneous Exercise: Ques No 15.

If A is square matrix such that A² = A, then (I + A)³ – 7A is equal to

(A) A

(B) I – A

(C) I

(D) 3A

NCERT Solutions:

C.

Since A² = A,

(I + A)³ – 7A

= I³ + A³ + 3IA(I + A) – 7A

= I + (A2)A + 3A(I + A) – 7A

= I + (A)A + 3A + 3A² – 7A

= I + A2 + 3A2 – 4A

= I + 4A2 – 4A

= I + 4A – 4A = I  

class 12 maths ncert solutionsmatricesmatrices class 12matrices class 12 ncert solutionsmatrix multiplicationncert solutionsncert solutions class 12ncert solutions class 12 mathsncert solutions class 12th mathsncert solutions class 12th maths pdfncert solutions for class 12ncert solutions for class 12 mathsorthogonal matrix