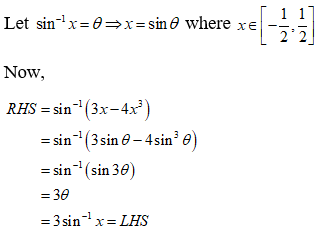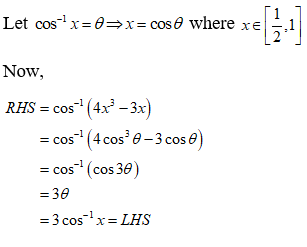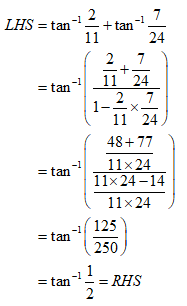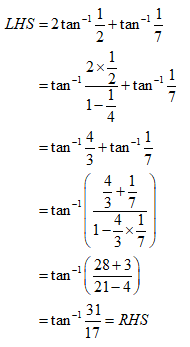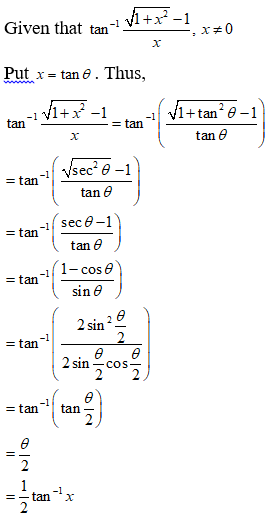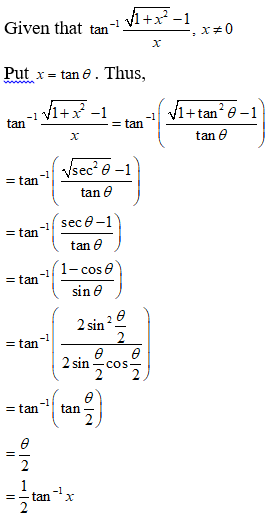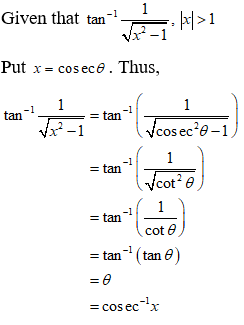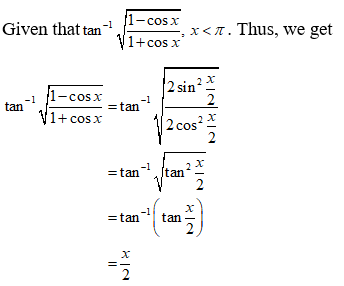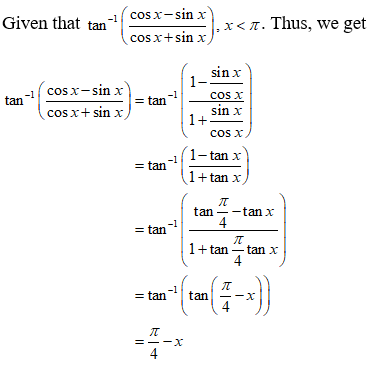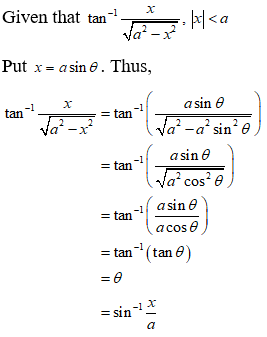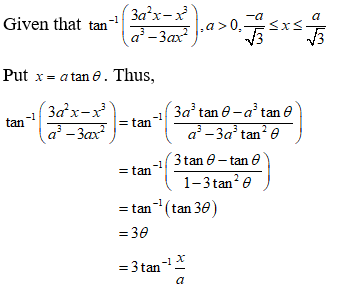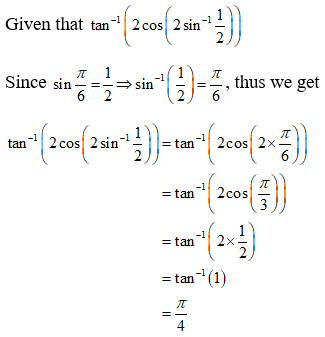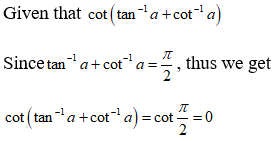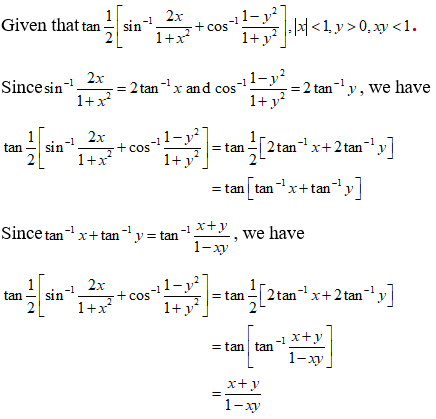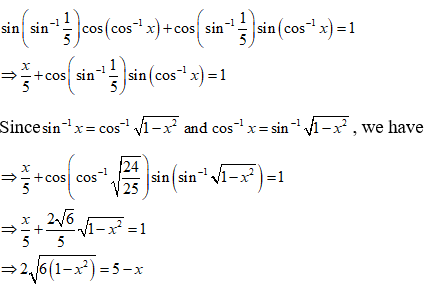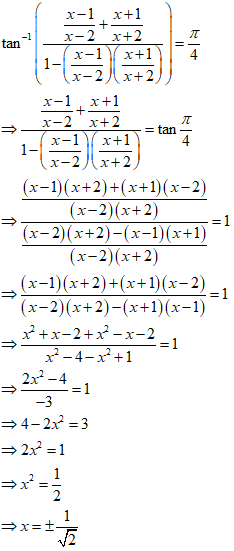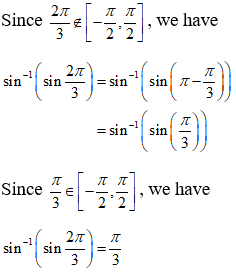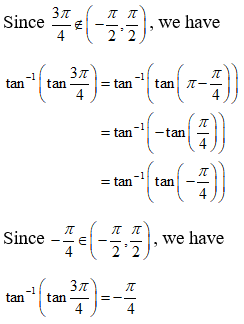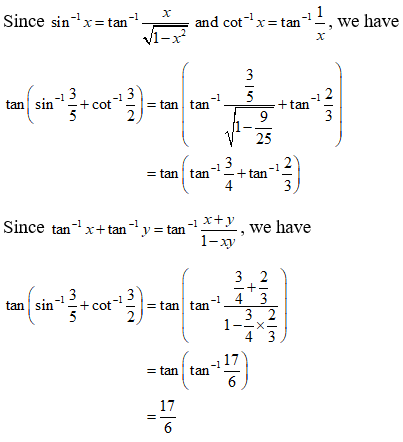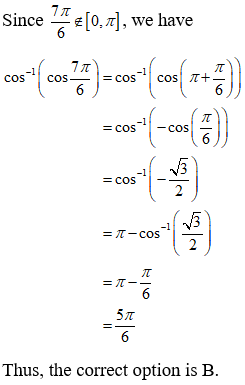NCERT Solutions for Class 12 Maths Inverse Trigonometry Functions
Hi Students, Welcome to Amans Maths Blogs (AMB). In this post, you will get the NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2. This NCERT Solutions can be downloaded in PDF file. The downloading link is given at last.
CBSE Class 12th is an important school class in your life as you take some serious decision about your career. And out of all subjects, Maths is an important and core subjects. So CBSE NCERT Solutions for Class 12th Maths is major role in your exam preparation as it has detailed chapter wise solutions for all exercise.
As we know that all the schools affiliated from CBSE follow the NCERT books for all subjects. You can check the CBSE NCERT Syllabus. Thus, NCERT Solutions helps the students to solve the exercise questions as given in NCERT Books.
NCERT Solutions for Class 12 Maths are not only the solutions of Maths exercise but it builds your foundation of other important subjects. Getting knowledge of depth concept of CBSE Class 12th Maths like Algebra, Calculus, Trigonometry, Coordinate Geometry help you to understand the concept of Physics and Physical Chemistry.
NCERT Solutions for Class 12 Maths Inverse Trigonometry Functions Exercise 2.2
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 1.
Prove that 3sin-1x = sin-1(3x – 4x3), where x ∈ [-1/2, 1/2]
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 2.
Prove that 3cos-1x = cos-1(4x3 – 3x), where x ∈ [1/2, 1]
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 3.
Prove that tan-1(2/11) + tan-1(7/24) = tan-1(1/2).
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 4.
Prove that 2tan-1(1/2) + tan-1(1/7) = tan-1(31/17).
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 5.
Write the function tan-1(√(1 + x2) – 1)/x, x ≠ 0 in simplest form.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 5.
Write the function tan-1(√(1 + x2) – 1)/x, x ≠ 0 in simplest form.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 6.
Write the function tan-1(1/√(x2 – 1)), |x| > 1 in simplest form.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 7.
Write the function tan-1√((1 – cos x)/(1 + cos x)), x < π in simplest form.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 8.
Write the function tan-1((cos x – sin x)/(cos x + sin x)), x < π in simplest form.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 9.
Write the function tan-1(x/√(a2 – x2)), |x| < a in simplest form.
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 10.
Write the function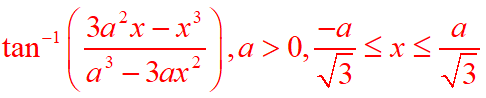
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 11.
Find the value of tan-1(2cos(2sin-1(1/2))).
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 12.
Find the value of cot(tan-1(a) + cot-1(a)).
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 13.
Find the value of .
NCERT Solutions:
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 14.
If sin(sin-1 1/5 + cos-1 x) = 1, then find the value of x.
NCERT Solutions:
Given that sin(sin-1 1/5 + cos-1 x) = 1.
Since sin(A + B) = sinAcosB + cosAsinB, we have
On squaring both sides, we get
⇒ 4[6(1 – x2)] = 25 + x2 – 10x
⇒ 24 – 24x2 = 25 + x2 – 10x
⇒ 25x2 – 10x + 1 = 0
⇒ (5x – 1)2 = 0
⇒ 5x – 1 = 0
⇒ x = 1/5
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 15.
If tan-1((x – 1)/(x + 2)) + tan-1((x + 1)/(x + 2)) = π/4, then find the value of x.
NCERT Solutions:
Given that tan-1((x – 1)/(x + 2)) + tan-1((x + 1)/(x + 2)) = π/4.
Since tan-1x + tan-1y = tan-1(x + y)/(1 – xy), we have
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 16.
Find the value of sin-1(sin2π/3).
NCERT Solutions:
Given that sin-1(2π/3).
We know that sin-1(sinx) = x if the principle value of sin-1x is x ∊ [-π/2, π/2].
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 17.
Find the value of tan-1(tan 3π/4).
NCERT Solutions:
Given that tan-1(tan 3π/4).
We know that tan-1(tan x) = x if the principle value of tan-1x is x ∊ (-π/2, π/2).
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 18.
Find the value of tan(sin-1 3/5 + cot-1 3/2).
NCERT Solutions:
Given that tan(sin-1 3/5 + cot-1 3/2).
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 19.
Find the value of cos-1(cos 7π/4).
(A) 7π/6 (B) 5π/6 (C) π/3 (D) π/6
NCERT Solutions:
Given that cos-1(cos-1 7π/4).
We know that cos-1(cosx) = x if the principle value of cos-1x is x ∊ [0, π].
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 20.
Find the value of sin(π/3 – sin-1(-1/2)).
(A) 1/2 (B) 1/2 (C) 1/4 (D) 1
NCERT Solutions:
Given that sin(π/3 – sin-1(-1/2)).
We know that sin-1(sinx) = x if the principle value of sin-1x is x ∊ [-π/2, π/2].
NCERT Solutions for Class 12 Maths Inverse Trigonometry Exercise 2.2: Ques No 21.
Find the value of tan-1√3 – cot-1 (-√3).
(A) π (B) -π/2 (C) 0 (D) 2√3
NCERT Solutions: