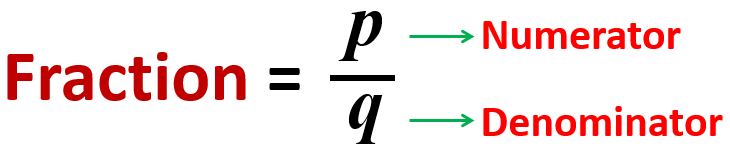Number System
In number system, first we need to understand the types of numbers so that we can use at our requirement in Mathematics.
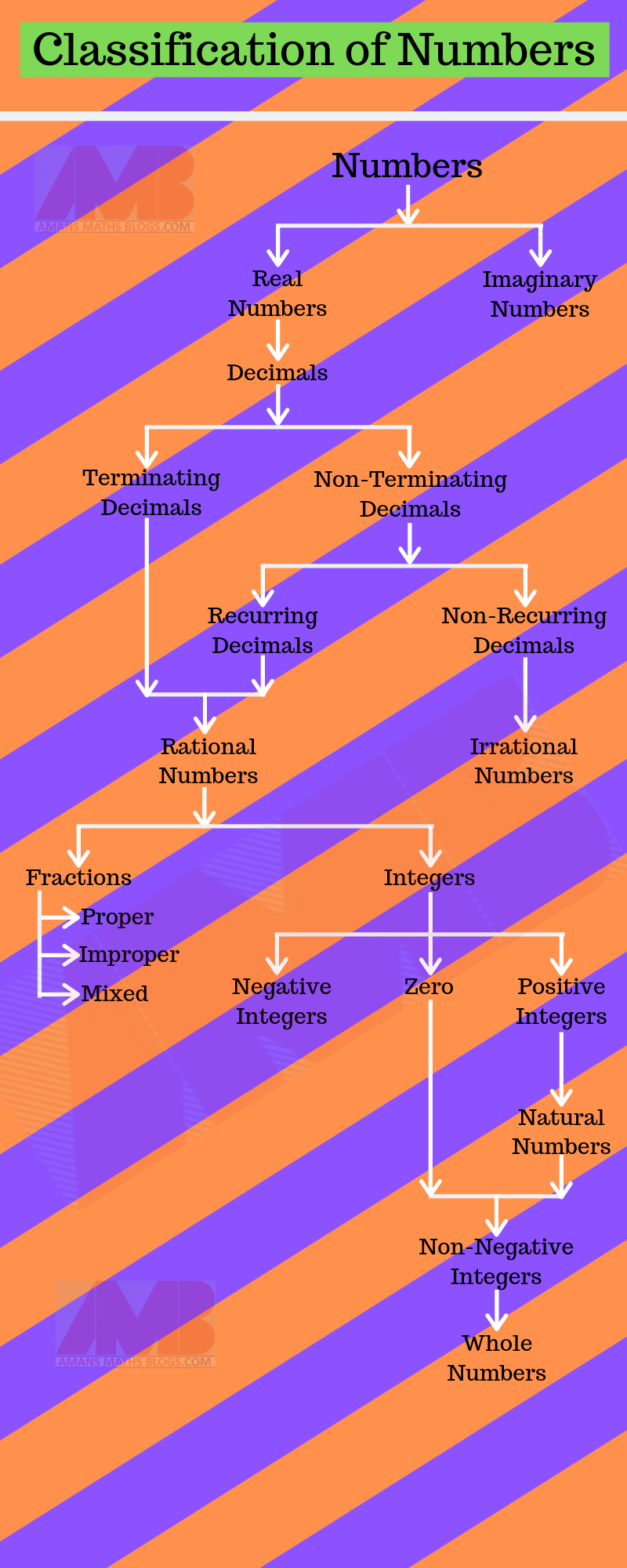
There are following types of numbers as shown in infographics below. Now, we understand them one by one, start from bottom to top, means natural numbers, whole numbers etc.
Natural Numbers
As we studied in Pre-school classes that the counting numbers are known as natural numbers. The natural numbers were the first number system developed and primarily used in counting.
The natural numbers are also called positive integers and start with 1. The natural numbers are denoted by N. The number of natural numbers are infinite.
Whole Numbers
In natural numbers, the numbers start with 1. There is no number used for nothing, means zero (0). Thus, when zero (0) is included in the set of natural numbers, then it is known as whole numbers. Hence, the whole numbers start with zero (0).
The set of whole numbers are denoted by W and it is also called as Non-Negative Integers. The number of whole numbers are infinite.
On comparing the sets of natural numbers N = {1, 2, 3, …} and whole numbers W = {0, 1, 2, 3, …}, we get that the natural numbers set is the subset of whole numbers. Thus, N ⊂ W.
Integers
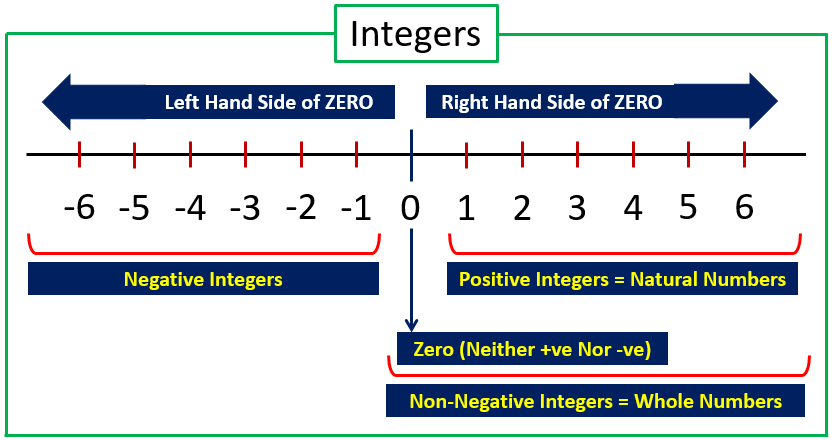
Integers are the set of natural numbers N = {1, 2, 3, ,…}, zero (0) and the negative of the natural numbers {-1, -2, -3, ,…}. Thus, the integers are {…, -3, -2, -1, 0, 1, 2, 3, …}. The set of the integers are denoted by Z (starting letter of German word ZAHLEN which means integers).
The natural numbers are also called positive integers and start with 1. The natural numbers are denoted by N. The number of natural numbers are infinite.
On comparing the sets of natural numbers N = {1, 2, 3, …}, whole numbers W = {0, 1, 2, 3, …} and the integers Z = {…, -3, -2, -1, 0, 1, 2, 3, …}, we get N ⊂ W ⊂ Z.
Read More : Full Details of Integers
Zero
Zero (0) is neither positive nor negative and it is located in between positive and negative integers on the number line.
Positive Integers
The set of positive integers is the natural numbers N = {1, 2, 3, …} which is located on the right hand side of zero on the number line.
Negative Integers
The set of negative integers is the negative of the natural numbers {-1, -2, -3, …] which is located on the left hand side of zero on the number line. The negative integers are less than zero.
Non-Negative Integers
The set of non-negative integers is the whole numbers Z = {0, 1, 2, 3, …}.
Rational Numbers
A number that can be written in the form of p/q where p and q are INTEGERS numbers and q ≠ 0 is known as rational numbers.
For example: 22/7, -16/7, 19/2, -25/3, 10/9 etc.
The set of the rational numbers are denoted by Q (starting letter of quotient).
Each integers can be written in the form of p/q. For example: 8 = 8/1 or -2 = -2/1. Thus, each integer is a rational numbers.
On comparing the sets of natural numbers N = {1, 2, 3, …}, whole numbers W = {0, 1, 2, 3, …} and the rational numbers Q = {…, -13/5, -12/7, 0, 5/3, 6,…}, we get N ⊂ W ⊂ Z ⊂ Q.
Read More : CBSE Class 8 Rational Numbers Notes
Irrational Numbers
A number that CANNOT be written in the form of p/q where p and q are INTEGERS numbers and q ≠ 0 is known as irrational numbers.
For example: π = 3.1415926535897932384626433832795… (and more), 1.20200200020000… etc
Fraction
A number that can be written in the form of p/q, where p and q are WHOLE numbers and q ≠ 0 is called as fraction. For example: 5/3, 2/5, 1/2, 2/9 etc.
Thus, by the definitions of rational numbers and fractions, we can say that:
In a fraction p/q (q ≠ 0), the number (p) written over the line known as NUMERATOR and the number (q) written below the line is known as DENOMINATOR is called as fraction.
Read More : Types of Fractions and Mathematical Operations of Fractions
Decimals
A decimal number is a number whose whole part and the fractional part are separated by decimal point.
For example: 2.3, 0.25, 3.654 etc.
In decimal number, as we move from the left to right, the place of the digits gets divided by 10.
Now, the decimals are following types:
Terminating Decimals
In the conversion of a fraction (p/q) into a decimal, when we get a remainder zero (0) in the division of the numerator p by the denominator q, then the decimal is terminated after some decimal places.
This types of decimal is known as the terminating decimals.
For example: 12/5 = 2.5, 24/3 = 8.0, 1/80 = 0.0125 etc.
Non-Terminating Decimals
In the conversion of a fraction (p/q) into a decimal, when we don’t get a remainder zero (0) at any step in the division of the numerator p by the denominator q, then the decimal is NOT terminated after some decimal places.
This types of decimal is known as the nonterminating decimals.
For example: 1/3 = 0.333…, 1.2563… etc.
Now, this nonterminating decimals are also two types known as recurring and nonrecurring decimals.
Read More : Identification of Terminating or Non-Terminating Decimals Without Division
Recurring Decimals
When we have a repeating digits after decimal point in the non-terminating, then it is known as recurring decimals.
For example: 1/3 = 0.333…, 1/6 = 0.1666… 1.23232323…., 1.785785785785…etc.
For example: 2.3, 0.25, 3.654 etc.
Non-Recurring Decimals
When we have NO repeating digits after decimal point in the non-terminating, then it is known as recurring decimals.
For example: 1.2658743…, 1.02528954…, 1.10100100010000… etc.
Real Numbers
The set of all rational and irrational numbers are known as real numbers.
For example: 1, 1/5, -1.25, 1.333, -25.3 18.25487… etc.
All the real numbers can be represented on a number line.
Read More : How To Represents A Real Number on Number Line
The square of a real numbers is always positive.
Imaginary Numbers
A number whose the square is negative is known as imaginary numbers.
For example: 2i, 3i, -6i etc
The imaginary numbers are used in complex number, which are in the form of a + ib.
Hence, these are types of numbers in number system.
There are some special numbers in number system like prime numbers, coprime numbers, composite numbers, perfect numbers etc. We will discuss in other posts.