Hi Students, welcome to Amans Maths Blogs (AMB). In this article, we will study about CBSE Class 7 Maths Chapter Integers. It is the notes of Integers chapter which help for the students who study in class 7 of CBSE or any affiliated school.

In this notes, we discuss about integers numbers, integers definition, positive integers, negative integers, natural numbers and whole numbers etc.

We also cover some properties of integers like commutative, associative and distributive on the mathematical operation of integers as addition of integers, subtractions of integers, multiplication of integers and division of integers etc.

So let discuss one by one.

Table of Contents

Integers

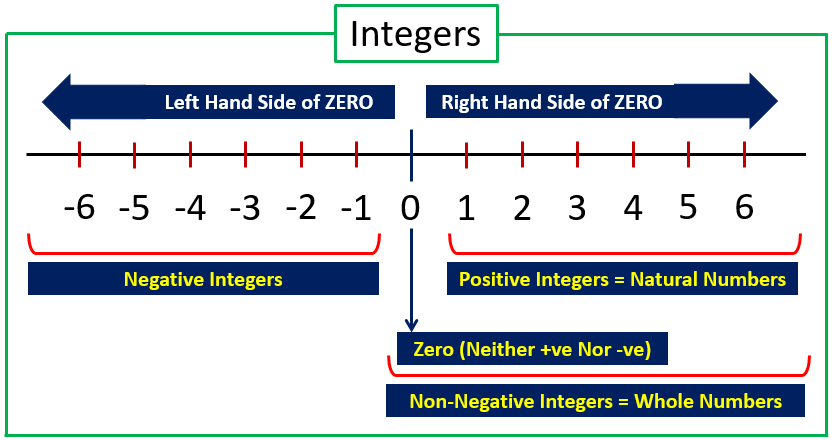
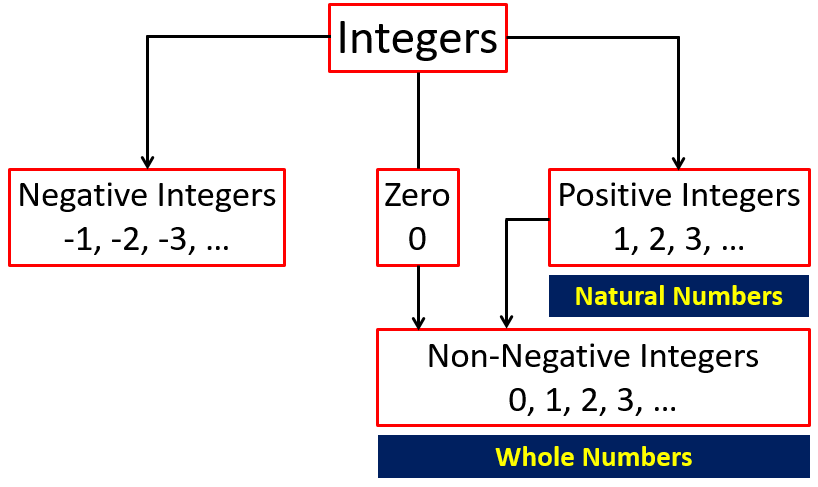
INTEGERS is the set of natural numbers (1, 2, 3, …), zero (0) and the negative of natural numbers (-1, -2, -3, …).

The integers are denoted by Z. Thus, Z = {…, -3, -2, -1, 0, 1, 2, 3, …}

Z stands for ZAHLEN, a German word, is used to denote integers.

Thus, integers is the set of

Positive Integers

Positive integers is the natural numbers (1, 2, 3, …) which is located on the right hand side of zero on the number line.

Negative Integers

Negative integers is the negative of the natural numbers (-1, -2, -3, …) which is located on the left hand side of zero on the number line. The negative integers are less than zero.

Zero

Zero (0) is neither positive nor negative and it is located in between positive and negative integers on the number line.

Operation of Integers

Addition of Integers

In the addition of integers, we use the following rules:

Rule 1 : To add two positive integers, we add the numbers and assign positive sign to the addition. It means, (+a) + (+b) = +(a + b).

For example: (+10) + (+15) = +25

Rule 2 : To add two negative integers, we add the numbers and assign negative sign to the addition. It means, (-a) + (-b) = -(a + b).

For example: (-10) + (-15) = -25

Rule 3 : To add one positive and one negative integers, we subtract the numbers and assign the sign of larger number to the difference. It means, (-a) + (+b) = -(a – b) if a > b and (-a) + (+b) = +(b – a) if b > a.

For example: (-10) + (+15) = +5, (-25) + (+23) = -2.

The summary of addition of integers as below:

Same sign: Add the numbers and assign the same sign

Different Sign: Subtract the numbers and assign larger number sign

Subtraction of Integers

In the subtraction of integers, we use the following rules:

Rule 1 : To subtract two positive integers, we subtract the numbers and assign the sign of larger number to the difference. It means, (+a) – (+b) = +(a – b) if a > b and (+a) – (+b) = -(b – a) if b > a.

For example: (+10) – (+15) = -5, (+20) – (+15) = +5

Rule 2 : To subtract two negative integers, we subtract the numbers and assign the sign of larger number to the difference. It means, (-a) – (-b) = -(a – b) if a > b and (-a) – (-b) = +(b – a) if b > a.

For example: (-10) – (-15) = +5, (-20) – (-15) = +5

Rule 3 : To subtract one positive and one negative integers, we add the numbers and assign the sign. It means, (+a) – (-b) = +(a + b) and (-a) – (+b) = -(a + b).

For example: (+10) – (-15) = +25, (-20) – (+15) = -35

The summary of subtraction of integers as below:

Same sign: Change the sign of second numbers and use addition rules

Different Sign: Change the sign of second numbers and use addition rules

Multiplication of Integers

In the multiplication of integers, we use the following rules:

Rule 1 : To multiply two positive integers, we multiply the numbers and assign positive sign to the product. It means, (+a) x (+b) = +(a x b).

For example: (+10) x (+15) = +150

Rule 2 : To multiply two negative integers, we multiply the numbers and assign positive sign to the product. It means, (-a) x (-b) = +(a x b).

For example: (-10) x (-15) = +150

Rule 3 : To multiply one positive and one negative integers, we multiply the numbers and assign negative sign to the product. It means, (-a) x (+b) = -(a x b) and (+a) x (-b) = -(a x b).

For example: (-10) x (+15) = -150, (+20) x (-5) = -100

The summary of multiplication of integers as below:

Same sign: Multiply the numbers and assign positive sign to the product

Different Sign: Multiply the numbers and assign negative sign to the product

Division of Integers

In the division of integers, we use the following rules:

Rule 1 : To divide two positive integers, we divide the numbers and assign positive sign to the quotient. It means, (+a) ÷ (+b) = +(a ÷ b).

For example: (+100) ÷ (+5) = +20

Rule 2 : To divide two negative integers, we divide the numbers and assign positive sign to the quotient. It means, (-a) ÷ (-b) = +(a ÷ b).

For example: (-100) ÷ (-5) = +20

Rule 3 : To divide one positive and one negative integers, we divide the numbers and assign negative sign to the quotient. It means, (-a) ÷ (+b) = -(a ÷ b) and (+a) ÷ (-b) = -(a ÷ b).

For example: (-150) ÷ (+15) = -10, (+20) ÷ (-5) = -4

The summary of division of integers as below:

Same sign: Divide the numbers and assign positive sign to the quotient

Different Sign: Divide the numbers and assign negative sign to the quotient

Properties of Integers

Properties of Addition of Integers:

Closure Property of Addition: Natural numbers, whole numbers and integers are closed under addition. It means, if we add two natural numbers, then we get the sum as a natural number, similarly for whole numbers and integers.

For example: 23 + 15 = 38; here 23 and 15 are natural numbers and their sum 38 is also a natural number.

Commutative Property of Addition : For two integers a and b, we have a + b = b + a. It means, the order of operation of addition on integers does not change the sum.

For example: 23 + 15 = 15 + 23 = 38

Associative Property of Addition : For three integers a, b and c, we have a + (b + c) = (a + b) + c. It means, the grouping of numbers does not change the sum

For example: 23 + (15 + 10) = (23 + 15) + 10 = 48

Distributive Over Addition Property : For three integers a, b and c, we have a(b + c) = ab + ac. It means, each integer inside the parenthesis is multiplied by the integer outside the parenthesis, then the resulting products are added together.

For example: 5(15 + 10) = (5 x 15) + (5 x 10) = 75 + 50 = 125

The summary of properties of addition of integers as below:

Closure: a + b = c, where a, b, c ∈ N, W, Z

Commutative: a + b = b + a

Associative: a + (b + c) = (a + b) + c

Distributive: a(b + c) = ab + ac

Properties of Subtraction of Integers:

Closure Property of Subtraction: Natural numbers and whole numbers are NOT closed under subtraction. It means, if we subtract two natural numbers, then the difference is not always natural number similarly for whole numbers. BUT, the integers are closed under subtraction. It means, if we subtract two integers, then the difference is always integers.

For example: 23 – 43 = -20; here 23 and 43 are integers and their difference -20 is also an integer.

Commutative Property of Subtraction : For two integers a and b, we have a – b ≠ b – a. It means, the subtraction does NOT hold the commutative.

For example: 23 – 15 ≠ 15 – 23

Associative Property of Addition : For three integers a, b and c, we have a – (b – c) = (a – b) – c. It means, the grouping of numbers changes the difference.

For example: 23 – (15 – 10) ≠ (23 – 15) – 10

Distributive Over Subtraction Property : For three integers a, b and c, we have a(b – c) = ab – ac. It means, each integer inside the parenthesis is multiplied by the integer outside the parenthesis, then find the difference of the resulting products.

For example: 5(15 – 10) = (5 x 15) – (5 x 10) = 75 – 50 = 25

The summary of properties of subtraction of integers as below:

Closure: a – b = c, where a, b, c ∈ Z

NOT Commutative: a + b ≠ b + a

NOT Associative: a – (b – c) ≠ (a – b) – c

Distributive: a(b – c) = ab – ac

Properties of Multiplication of Integers:

Closure Property of Multiplication: Natural numbers, whole numbers and integers are closed under multiplication. It means, if we add two natural numbers, then we get the product as a natural number, similarly for whole numbers and integers.

For example: 23 x 10 = 230; here 23 and 10 are natural numbers and their product 230 is also a natural number.

Commutative Property of Multiplication : For two integers a and b, we have a x b = b x a. It means, the order of operation of multiplication on integers does not change the product.

For example: 23 x 10 = 10 x 23 = 230

Associative Property of Multiplication : For three integers a, b and c, we have a x (b x c) = (a x b) x c. It means, the grouping of numbers does not change the product.

For example: 3 x (15 x 10) = (3 x 15) x 10 = 450

The summary of properties of multiplication of integers as below:

Closure: a x b = c, where a, b, c ∈ N, W, Z

Commutative: a x b = b x a

Associative: a x (b x c) = (a x b) x c

Additive Identity

If we add zero (0) to any integers, then the value of the integers does not change.

It means a + 0 = 0 + a = a.

Zero (0) is known as Additive Identity

For example: 23 + 0 = 0 + 23 = 23

Additive Inverse

If the sum of two numbers is zero (0), then each of the numbers is additive inverse of each other.

It means a + b = 0 ⇒ b = -a.

Additive Inverse of a = -a

Additive Inverse of -a = a

For example: 23 + (-23) = 0

Multiplicative Identity

If we multiply one (1) to any integers, then the value of the integers does not change.

It means a x 1 = 1 x a = a.

One (1) is known as Multiplicative Identity

For example: 23 x 1 = 1 x 23 = 23

Multiplicative Inverse

If the product of two numbers is one (1), then each of the numbers is multiplicative inverse of each other.

It means a x b = 1 ⇒ b = 1/a.

Multiplicative Inverse of a = 1/a

Multiplicative Inverse of 1/a = a

For example: 23 x (1/23) = 1

BODMAS Rule

To learn about BODMAS rule, Click Here.