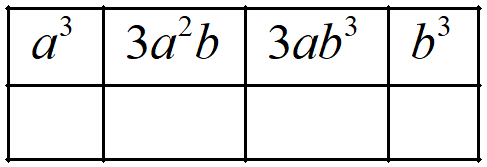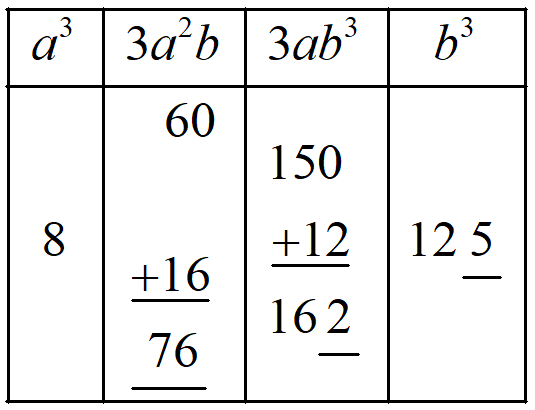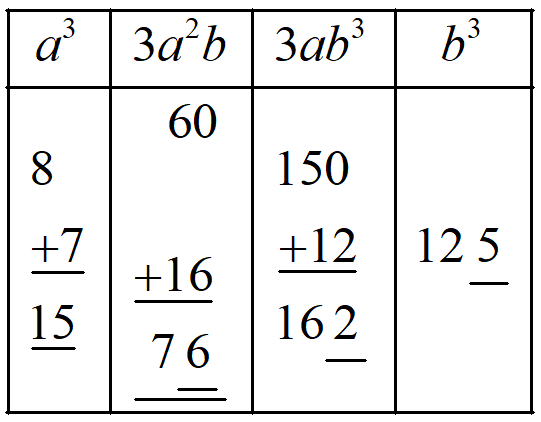Cube And Cube Roots
Hi Students, welcome to Amans Maths Blogs (AMB). In this article, CBSE Class 8 Maths Chapter Cube and Cube Roots is explained. It is the notes of Cube and Cube Roots chapter which help for the students who study in class 8 of CBSE or any affiliated school.
We have studied about Square and Square Roots, how to find the squares and square root of a number. Now, we learn about the Cubes and Cube Roots in this article.
Cube of a number is the multiplication of the numbers with itself three times.
Cube Root of a number is the number that gives n when it is multiplied by itself.
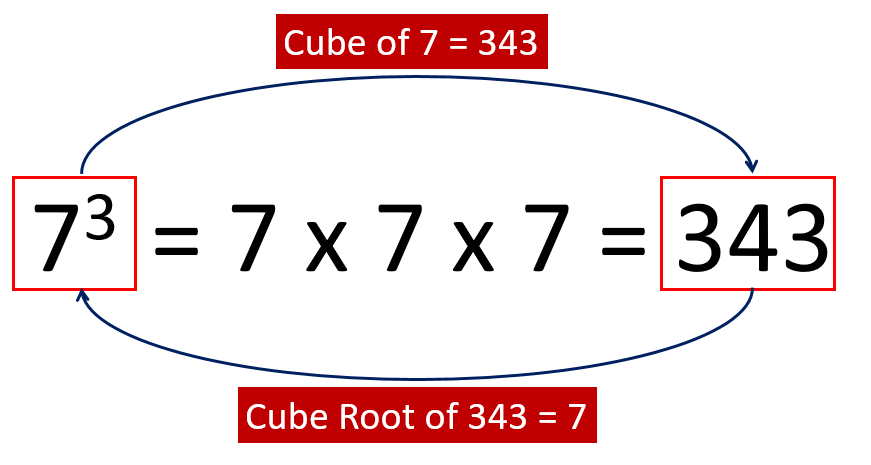
For example: Cube of 7 is 343 and Cube Root of 343 is 7, explained as below.
To check whether a natural number is a perfect cube or not, we do the prime factorization of the natural number. If all the primes in prime factorization are in pair of three, then it is a perfect cube number otherwise not.
For example: 1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3 = (2 x 2 x 2) x (2 x 2 x 2) x (3 x 3 x 3), here all the primes in the prime factorization are in pair of three, so 1728 is a perfect cube number.
Cube of Rational Numbers
The cube of a rational number (p/q, q ≠ 0) is the ratio of cube of its numerator and the cube of its denominator.
Read : Rational Numbers Notes and Facts
Properties of Cube Numbers
There are following properties of cube numbers:
Property 1: Cube of a negative integer is always a negative integer.
For example : (-3)3 = (-3) x (-3) x (-3) = -27
Property 2: Cubes of all even number are even.
For example : 43 = 4 x 4 x 4 = 64. Here, 4 is even and 64 is also an even number.
Property 3: Cubes of all odd number are odd.
For example : 53 = 5 x 5 x 5 = 125. Here, 5 is odd and 125 is also an odd number.
Property 4: The sum of cubes of first n natural numbers is equal to the squares of their sum. it means,
For example : 13 + 23 + 33 + … + 103 = (10(10 + 1)/2)2 = 166375
Property 5: The cube of a natural number of the form (3m + 1) is a natural number of the same form.
For example : (25)3 = (3 x 8 + 1)3 = 15625 = (3 x 5208 + 1). Here, 25 and 15625 both are of the form of (3m + 1).
Property 6: The cube of a natural number of the form (3m + 2) is a natural number of the same form.
For example : (11)3 = (3 x 3 + 2)3 = 1331 = (3 x 443 + 2). Here, 11 and 1331 both are of the form of (3m + 2).
Property 7: Cube of a natural number which is a multiple of 3 is the multiple of 27.
For example : (12)3 = 1728 = (17 x 64). Here, 12 is the multiple of 3 and 1728 is the multiple of 27.
Property 8: Cubes of the numbers ending with the digits 0, 1, 4, 5, 6, and 9 are the numbers ending with the same digit.
For example : (11)3 = 1331. Here, 11 is ending at 1 and 1331 is also ending at 1.
Property 9: Cubes of the numbers ending with zero (0) are the numbers ending three zeroes (000).
For example : (10)3 = 1000. Here, 10 is ending at 0 and 1000 is ending at three zeroes (000).
Property 10: Cube of a number ending with the digit 2 are the numbers ending with 8 and the cube of a number ending with 8 are the numbers ending with 2.
For example : (12)3 = 1728: Here, 12 is ending at 2 and 1728 is ending at 8. (8)3 = 512: Here, 8 is ending at 8 and 512 is ending at 2.
Property 11: Cube of a number ending with the digit 3 are the numbers ending with the digit 7 and similarly, the cube of a number ending with the digit 7 are the numbers ending with the digit 3.
For example : (13)3 = 2197: Here, 13 is ending at 3 and 2197 is ending at 7. (17)3 = 4913: Here, 17 is ending at 7 and 4913 is ending at 3.
Property 12: A perfect cube is the sum of the consecutive odd numbers. The consecutive odd numbers whose the sum makes up a perfect cube. Themselves appear in the order of odd numbers of the number line.
For example :
13 = 1 = 1
23 = 8 = 3 + 5
33 = 27 = 7 + 9 + 11
43 = 64 = 13 + 15 + 17 + 19
53 = 125 = 21 + 23 + 25 + 27 + 29 etc.
Cubes From 1 to 30
There are cubes from 1 to 30 as below.
| Number | Cubes of Number | Number | Cubes of Number | Number | Cubes of Number |
|---|---|---|---|---|---|
| 1 | 1 |
11 | 1331 |
21 | 9261 |
| 2 | 8 |
12 | 1728 |
22 | 10648 |
| 3 | 27 |
13 | 2197 |
23 | 12167 |
| 4 | 64 |
14 | 2744 |
24 | 13824 |
| 5 | 125 |
15 | 3375 |
25 | 15625 |
| 6 | 216 |
16 | 4096 | 26 | 17576 |
| 7 | 343 |
17 | 4913 | 27 | 19683 |
| 8 | 512 |
18 | 5832 |
28 | 21952 |
| 9 | 729 |
19 | 6859 | 29 | 24369 |
| 10 | 1000 |
20 | 8000 |
30 | 27000 |
Method To Find Cube of a Number
There are following method to find cube of a number:
Multiplication Method To Find the Cube of a Number
To find the Cube of a number, we multiply the given number with itself three times. It means,
For example : (9)3 = 9 x 9 x 9 = 729.
Column Method To Find the Cube of a Number
In column method of finding cube of a number, we use (a + b)3 = a3 + 3a2b + 3ab2 + b3. This method is used to find the cube of two-digits natural number.
Let we need to find the cube of 25 by using column method.
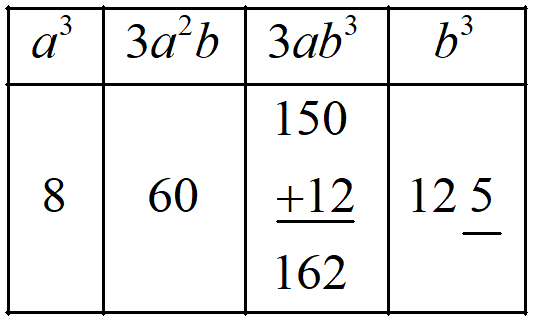
Step 1: Take a = 2 and b = 5, then write the values of a3, 3a2b, 3ab2 and b3 in three columns.
Step 2: Now, underline the unit digit of b3 and add the remaining values to the column of 3ab2.
Step 3: Again now, underline the unit digit of values of 3a2b and the remaining values to the column of 3ab2.
Step 4: Underline the unit digit of the values of 3a2b and add the remaining values to the column of a3. and then underline its whole values.
Step 5: Write the underlined digits and this is the cube of the number ab = 25. Thus, 253 = 15625.
Cube Roots
A number N is called the cube root of M if N = M3 and the cube root of N is denoted by ∛N.
Cube root of a negative number is a negative number. It means, ∛(-N) = – ∛N.
Read : Algebraic Expressions and Identities
For two integers, m and n, ∛(mn) = ∛m x ∛n.
For two integers, n ≠ 0, ∛(m/n) = ∛m / ∛n
Short Method to Find Cube Root
Cube Roots by Subtraction
To understand this, start with as below.
13 – 03 = 1 – 0 = 1
23 – 13 = 8 – 1 = 7
33 – 23 = 27 – 8 = 19
43 – 33 = 64 – 27 = 37
53 – 43 = 125 – 64 = 61
63 – 53 = 216 – 125 = 91
73 – 63 = 343 – 64 = 127
83 – 73 = 512 – 343 = 169
93 – 83 = 729 – 512 = 217 etc.
Thus, to find the cube root of a perfect cube number, subtract the numbers 1, 7, 19, 37, 61, 91, 127, 169, 271, 331, 397 … etc from the perfect cube until we get zero. Then the number of the step of the subtraction will be cube root of the perfect cube number.
For example: Let we need to find the cube root of 125.
Then,
125 – 1 = 124
124 – 7 = 117
117 – 19 = 98
98 – 37 = 61
61 – 61 = 0
After 5 steps, we get the subtraction as zero. Thus, ∛125 = 5.
Read : Linear Equations in One Variable
Cube Roots of Perfect Cube Using Unit Digit
To understand this, start with as below.
| Unit Digit of Number | Unit Digit of Cube Root of Number |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 3 | 7 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 3 |
| 8 | 2 |
| 9 | 9 |
Let we need to find the cube root of 2197.
Step 1: Find the unit digit in the cube root of given number (2197) using the table above.
From the table, we get that the unit digit of cube root of 2197 = 3.
Step 2: Strike out the units, tens and hundreds digits of the number. If no digits are left, then the digit obtained in Step 1 is the required cube root of the given number.
After striking out units (7), tens (9) and hundred (1) of 2197, we get 2.
Step 3: Now, the number in Step 2, find the largest single digit number whose cube root is less than or equal to this left over number. This number is the tens digit of the cube root.
In Step 2, we get the left number as 2. Since 1 is the largest single digit number whose cubes is less than 2. Thus, the tens digit of the cube root is 1.
Step 4: Obtain the required cube root by forming a number in Step and tens digit is the number obtained in Step 3.
Thus, the required cube root of 2197 is 13. Hence, ∛2197 = 13.
If you want to buy the Pearson Books Series (Physics, Chemistry, Biology & Maths) for Class 8,
Now, let we need to find the cube root of 456533.
Step 1: Find the unit digit in the cube root of given number (456533) using the table above.
From the table, we get that the unit digit of cube root of 456533 = 7.
Step 2: Strike out the units, tens and hundreds digits of the number. If no digits are left, then the digit obtained in Step 1 is the required cube root of the given number.
After striking out units (3), tens (3) and hundred (5) of 456533, we get 456.
Step 3: Now, the number in Step 2, find the largest single digit number whose cube root is less than or equal to this left over number. This number is the tens digit of the cube root.
In Step 2, we get the left number as 456. Since 73 = 343 < 456 and 83 = 512 > 456, 73 = 343 < 456 is the largest single digit number whose cubes is less than 456. Thus, the tens digit of the cube root is 7.
Step 4: Obtain the required cube root by forming a number in Step and tens digit is the number obtained in Step 3.
Thus, the required cube root of 456533 is 77. Hence, ∛456533 = 77.
Cube Roots of Perfect Cube Using Prime Factorization
First, we do the prime factorization of the given number and then group the factors in triplets such that all the three factors in each triplet are equal.
Take one factor from each triplet and find the their product. Let we need to find the cube root of 1728.
Then, first we do the prime factorization of 1728. We get as 1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3.
Now, we group them as 1728 = (2 x 2 x 2) x (2 x 2 x 2) x (3 x 3 x 3).
Thus, the cube root of 1728 is ∛1728 = 2 x 2 x 3 = 12.