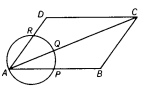
Cyclic Quadrilateral
If ABCD is a cyclic quadrilateral, then the sum of opposite angles is 180 degrees. It means, ∠A + ∠C = ∠B + ∠D = 180 degrees.
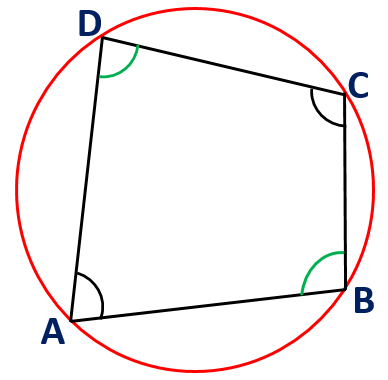
Product of Diagonals : Ptolemy Theorem
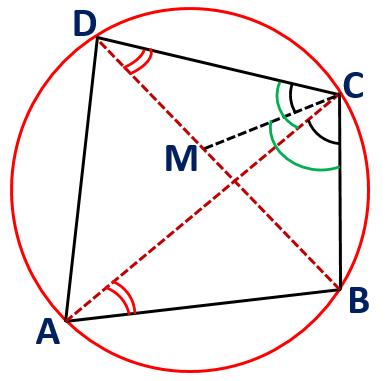
In a cyclic quadrilateral, the sum of product of two pairs of opposite sides equals the product of two diagonals. This property of cyclic quadrilateral is known as PTOLEMY THEOREM.
If ABCD is a cyclic quadrilateral, then AB x CD + AB x BC = AC x BD.
Proof:
Take a point M on BD so that ∠ACB = ∠MCD.
As we know that the angles in same segment are equal. Then, ∠BAC = ∠BDC.
Now by AA Similarity, we have ∆ACB ~ ∆DCM.
Thus, we get ⇒ AB x CD = AC x DM … (1)
Now, ∠DAC = ∠DBC and ∠DCA = ∠BCM, then by AA similarity, we have ∆ACD ~ ∆BCM.
Thus, we get ⇒ AD x BC = AC x BM … (2)
From (1) + (2), we get AB x CD + AD x BC = AC x BD.
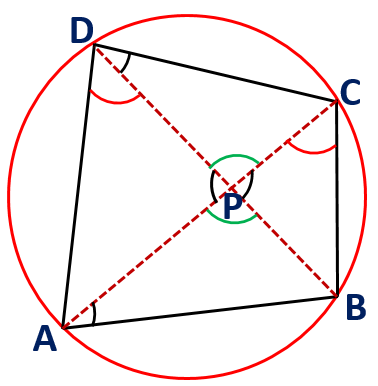
Ratio of Diagonals
In a cyclic quadrilateral, the ratio of the diagonals equals the ratio of the sum of products of sides that share the diagonal’s end points.
If ABCD is a cyclic quadrilateral, then .
Proof:
Let ABCD is a cyclic quadrilateral whose diagonals intersect at P.
As we know that the angles in same segment are equal. Then, ∠BAC = ∠BDC and ∠ADB = ∠ACB.
From vertically opposite angles, ∠APB = ∠CPD and ∠APD = ∠BPC.
Now, by AA similarity, we have ∆PAD ~ ∆PBC.
Then, we get .
From first two ratios, ⇒
Multiplying both sides by AB, we get
⇒ … (1)
From last two ratios, ⇒
Multiplying both sides by CD, we get
⇒ … (2)
Now again, by AA similarity, we have ∆PAB ~ ∆PDC.
Then, we get .
From first two ratios, ⇒
Multiplying both sides by AD, we get
⇒ … (3)
From (1), (2), (3), we get .
Since ,
Adding (1st and 3rd Ratios) and (2nd and 4th Ratios)
⇒
Thus, we get
Important Questions And Answer
Ques 1 : In a triangle ABC, AB = 7, AC = 8, BC = 9. A point D is on its circumcircle such that AD bisects angle BAC. Then the value of AD/CD is
Ans : 5/3
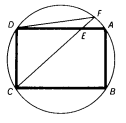
Ques 2 : E is a point on side AD of rectangle ABCD, so that DE = 6, while DA = 8, and DC = 6. If CE extended meets the circumcircle of the rectangle at F, find the measure of chord D.
Ans :
Ques 3 : On side AB of square ABCD, right triangle ABF, with hypotenuse AB, is drawn externally to the square. If AF = 6 and BF = 8 find EF, where E is the point of intersection of the diagonals of the square.
Ans :
Ques 4 : Point P on side AB of right triangle ABC is placed so that BP = PA = 2. Point Q is on hypotenuse AC so that PQ is perpendicular to AC. If CB = 3, find the measure of BQ, using Ptolemy’s Theorem.
Ans :
Ques 5 : If any circle passing through vertex A of parallelogram ABCD intersects sides AB, and AD at points P and R, respectively, and diagonal AC at point Q, prove that (AQ)(AC) = (AP)(AB) + (AR)(AD).
Ans :
Ques 6 : Diagonals AC and BD of quadrilateral ABCD meet at E. If AE = 2, BE = 5, CE = 10, DE = 4, and BC = 15/2 find AB.
Ans :
Ques 7 : If isosceles triangle ABC (AB = AC) is inscribed in a circle, and a point P is on BC. Prove that PA/(PB + PC) = AC/BC a constant rate for the given triangle.
Ans :