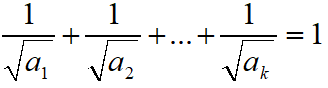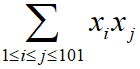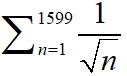Pre RMO 2019
Pre RMO 2019 is the first stage exam for Math Olympiad Exams. It was scheduled on 11 August 2019 at 10 AM to 1 PM.
Read: Get More Details About Pre RMO
Pre RMO 2019 Question Paper
Pre RMO 2019 conducted on 11 August 2019.
Pre RMO 2019 Answer Keys
Read: Pre RMO and RMO Important Study Materials: Books | PDFs | Blogs | YouTube Channels | Solved Papers
| Pre RMO 2019 |
|||||||
|---|---|---|---|---|---|---|---|
| Answer Keys | |||||||
| Ques No | Ans Key | Ques No | Ans Key | Ques No | Ans Key | Ques No | Ans Key |
| 1 | 04 | 9 | 14 | 17 | 30 | 25 | 48 |
| 2 | 13 | 10 | 55 | 18 | 20 | 26 | 50 |
| 3 | 13 | 11 | 06 | 19 | 13 | 27 | 84 |
| 4 | 36 | 12 | 18 | 20 | Bonus | 28 | 15 |
| 5 | 10 | 13 | 10 | 21 | 17 | 29 | 47 |
| 6 | 29 | 14 | 53 | 22 | 78 | 30 | 64 |
| 7 | 51 | 15 | 45 | 23 | 55 | ||
| 8 | 49 | 16 | 40 | 24 | 37 | ||

Pre RMO 2019 Solutions
Pre RMO 2019 Question No 1
From a square with sides of length 5, triangular pieces from the four corners are removed to form a regular octagon. Find the area removed to the nearest integer?
Solution:
Pre RMO 2019 Question No 2
Let f(x) = x2 + ax + b. If for all nonzero real x, and roots of f(x) = 0 are integers, what is the value of a2 + b2.
Read More : Pre RMO 2019 Results & Cut Off Marks
Solution:
Pre RMO 2019 Question No 3
Let x1 be a positive real number and for every integer n >=1 let xn+1 = 1 + x1x2 + … + xn-1xn. If x5 = 43, what is the sum of the digits of the largest prime factor of x6?
Solution:
Pre RMO 2019 Question No 4
An ant leaves the anthill for its morning exercise. It walks 4 feet east and then makes a 160 degree turn to the right and walks 4 more feet. It then makes another 160 degree turn to the right and walks 4 more feet. If the ant continues this pattern until it reaches the anthill again, what is the distance in feet it would have walked?
Solution:
Pre RMO 2019 Question No 5
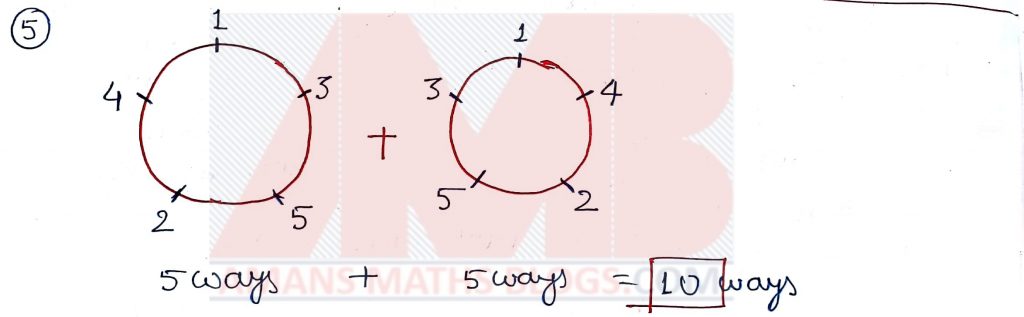
Five persons wearing badges with numbers 1, 2, 3, 4, 5 are seated on 5 chairs around a circular table. In how many ways can they be seated so that no two persons whose badges have consecutive numbers are seated next to each other? (Two arrangements obtained by rotation around the table are considered different.)
Solution:
Pre RMO 2019 Question No 6
Let abc be a three digit number with nonzero digits such that a2 + b2 = c2. What is the largest possible prime factor of abc?
Solution:
Pre RMO 2019 Question No 7
On a clock, there are two instants between 12 noon and 1 PM, when the hour hand and the minute hand are at right angles. The difference in minutes between these two instants is written as a + b/c, where a, b, c are positive integers, with b < c and b/c in the reduced form. What is the value of a + b + c?
Solution:
Pre RMO 2019 Question No 8
How many positive integers n are there such that 3 ≦ n ≦ 100 and is divisible by x2 + x + 1?
Solution:
Pre RMO 2019 Question No 9
Let the rational number p/q be closest to but not equal to 22/7 among all rational numbers with denominator less than 100. What is the value of p – 3q?
Solution:
Pre RMO 2019 Question No 10
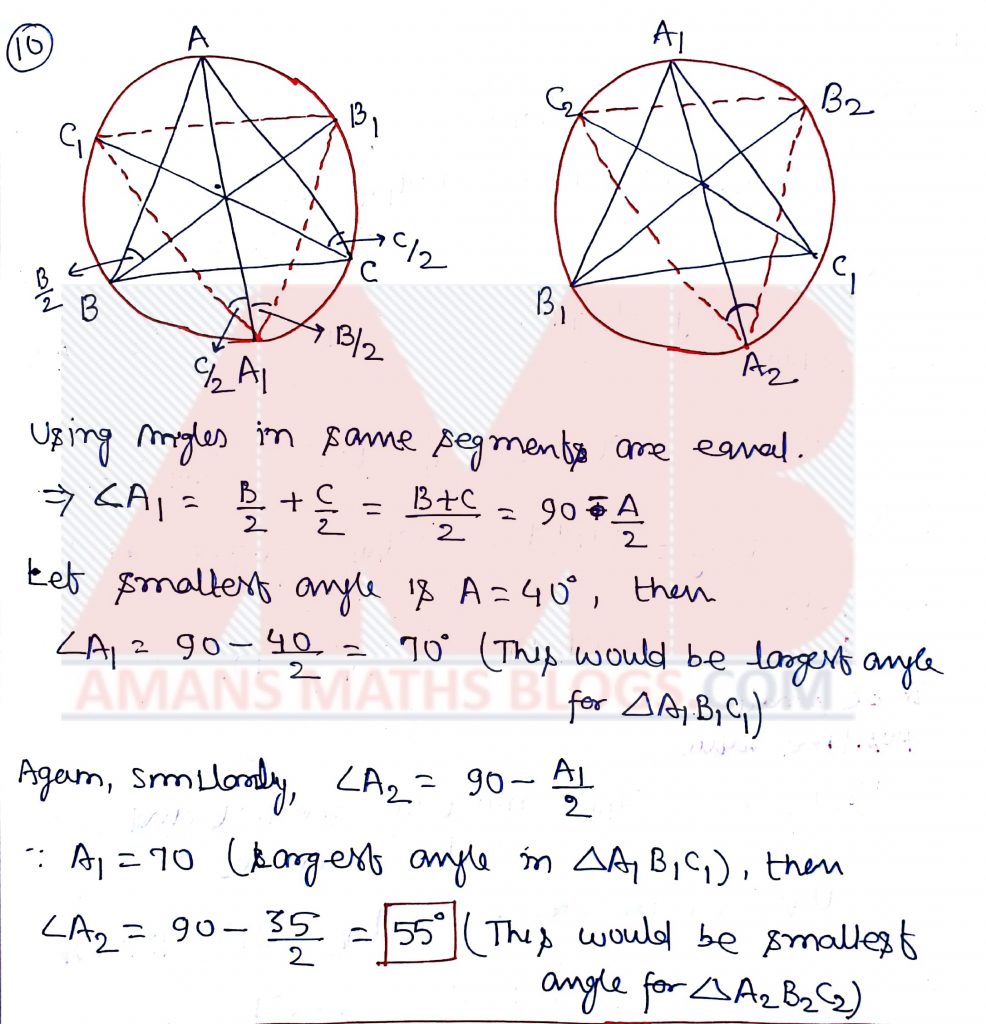
Let ABC be a triangle and let Ω be its circumcircle. The internal bisector of angles A, B and C intersect Ω at A1, B1 and C1 respectively and the internal bisector of angles A1, B1 and C1 of the triangle A1B1C1 intersect Ω at A2, B2 and C2 respectively. If the smallest angle of triangle ABC is 40 degree, what is the magnitude of the smallest angle of triangle A2B2C2 in degree?
Solution:
Pre RMO 2019 Question No 11
How many distinct triangles ABC are there up to similarity such that the magnitude of the angles A, B and C in degrees are positive integers and satisfy cosAcosB + sinAsinBsin kC = 1 for some positive integer k, where kC does not exceed 360 degree?
Solution:
Pre RMO 2019 Question No 12
A natural number k > 1 is called good if there exist natural numbers a1 < a2 < a3 < … < ak such that
Let f(n) be the sum of the first good numbers, n >= 1. Find the sum of all values of n for which f(n + 5) / f(n) is an integer.
Solution:
Pre RMO 2019 Question No 13
Each of the numbers x1, x2, x3, …, x101 is ±1. What is the smallest positive value of
Solution:
Pre RMO 2019 Question No 14
Find the smallest positive integer n >=10 such that (n + 6) is a prime and 9n + 7 is a perfect square.
Solution:
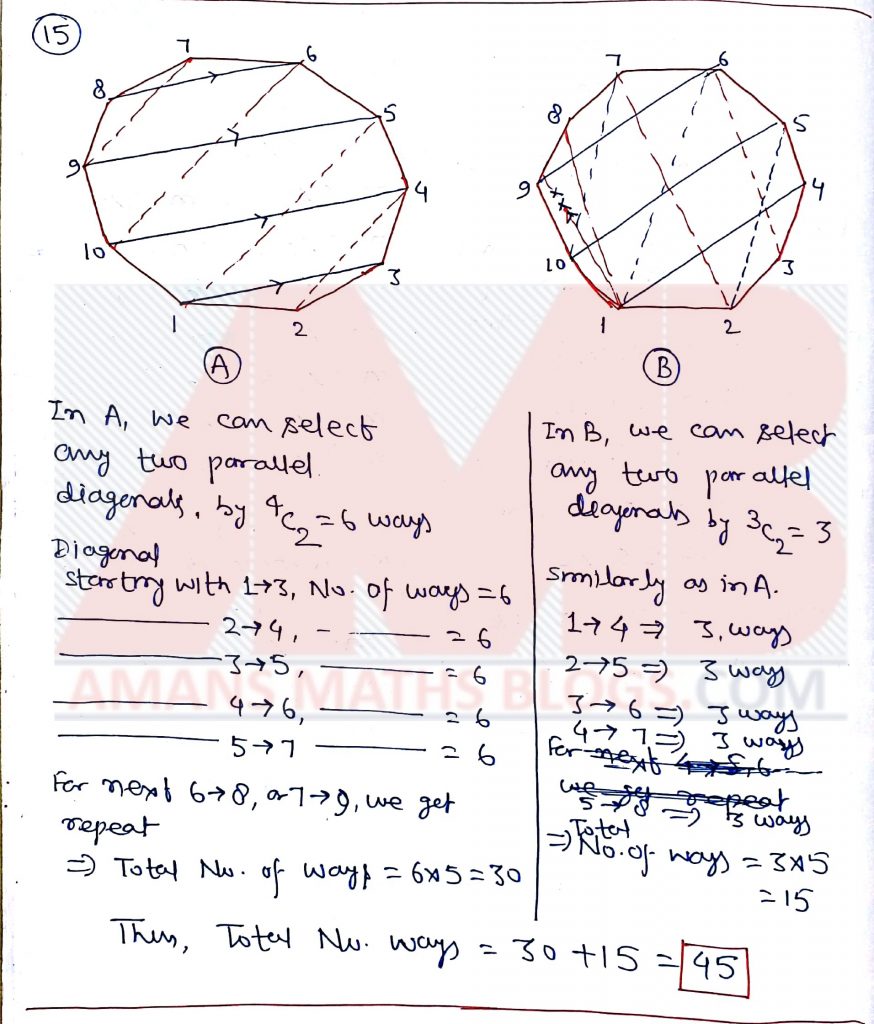
Pre RMO 2019 Question No 15
In how many ways can a pair of parallel diagonals of a regular polygon of 10 sides be selected?
Solution:
Pre RMO 2019 Question No 16
A pen costs Rs. 13 and note book costs Rs. 17. A school spends exactly Rs. 10000 in the year 2017-18 to buy x pens and y note books such that x and y are as close as possible (i.e., |x – y| minimum). Next year, in 2018-19, the school spends a little more than Rs. 10000 and buys y pens and x note books. How much more did the school pay?
Solution:
Pre RMO 2019 Question No 17
Find the number of ordered triples (a,b,c) of positive integer such that 30a + 50b + 70c ≦ 343.
Solution:
Pre RMO 2019 Question No 18
How many ordered pairs (a,b) of positive integers with a < b and 100 ≦ a,b ≦ 1000 satisfy gcd(a,b) : lcm(a,b) = 1 : 495?
Solution:
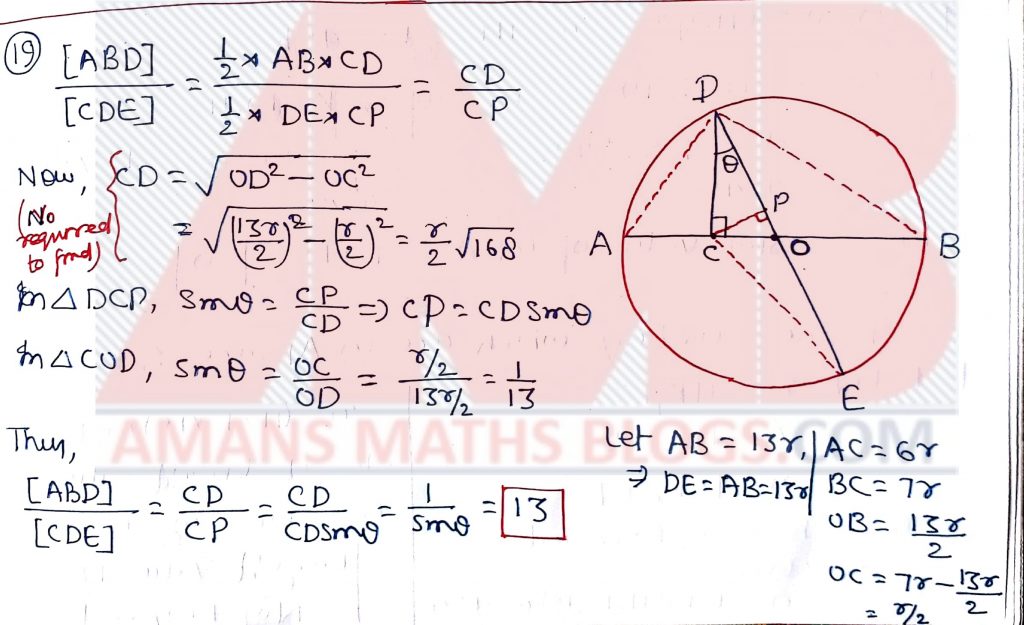
Pre RMO 2019 Question No 19
Let AB be a diameter of a circle and let c be a point on the segment AB such that AC : CB = 6 : 7. Let D be a point on the circle such that DC is perpendicular to AB. Let DE be the diameter through D. If [XYZ] denotes the area of the triangle XYZ find [ABD]/[CDE] to the nearest integer.
Solution:
Pre RMO 2019 Question No 20
Consider the set E of all natural numbers n such that when divided by 11, 12, 13, respectively, the remainders, in that order are distinct prime numbers in an arithmetic progression. If N is the largest number in E, find the sum of digits of N.
Solution:
Pre RMO 2019 Question No 21
Consider the set E = {5,6,7,8,9} for any partition {A,B} of E, with both a and B nonempty, consider the number obtained by adding the product of elements of A to the product of elements of B. Let N be the largest prime number among these numbers. Find the sum of the digits of N.
Solution:
Pre RMO 2019 Question No 22
What is the greatest integer not exceeding the sum
Solution:
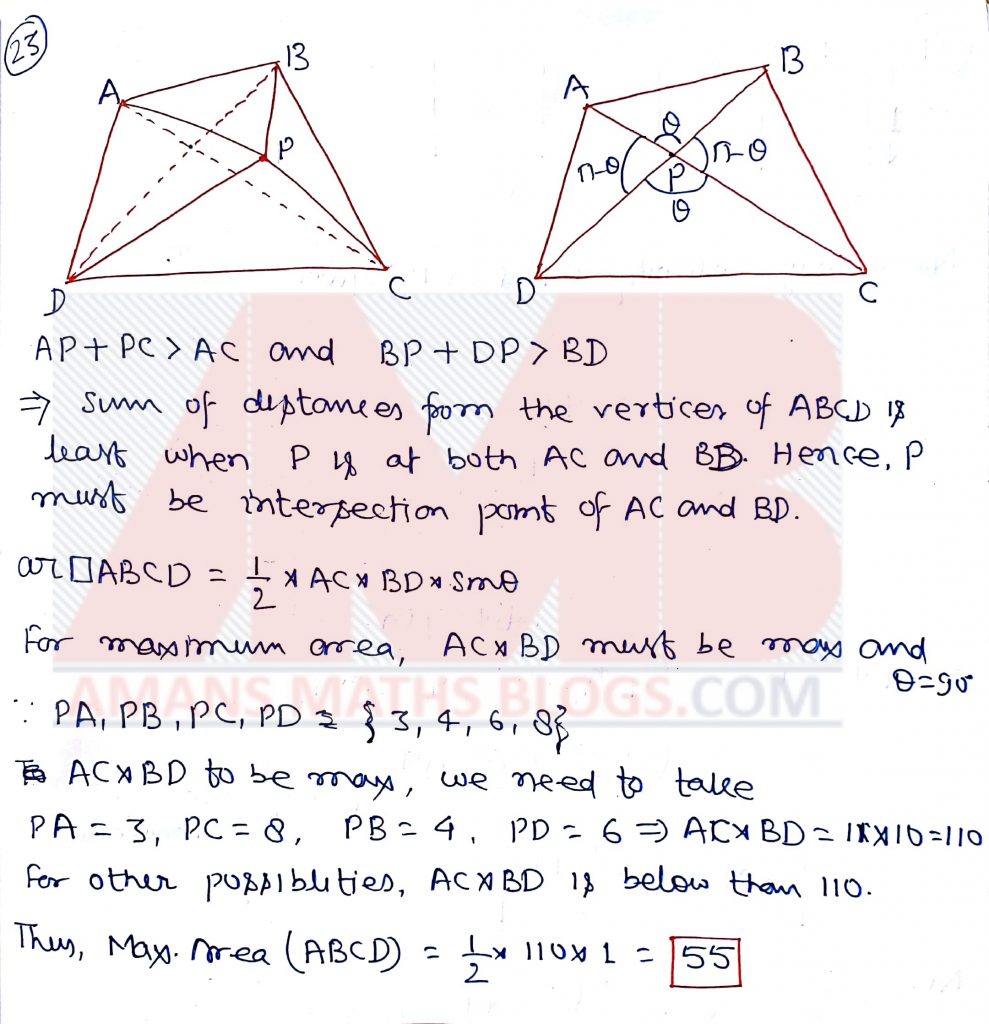
Pre RMO 2019 Question No 23
Let ABCD be a convex cyclic quadrilateral. Suppose P is a point is the plane of the quadrilateral such that the sum of its distances from the vertices of ABCD is the least. If {PA,PB.PC.PD} = {3,4,6,8}, what is the maximum possible area of ABCD?
Solution:
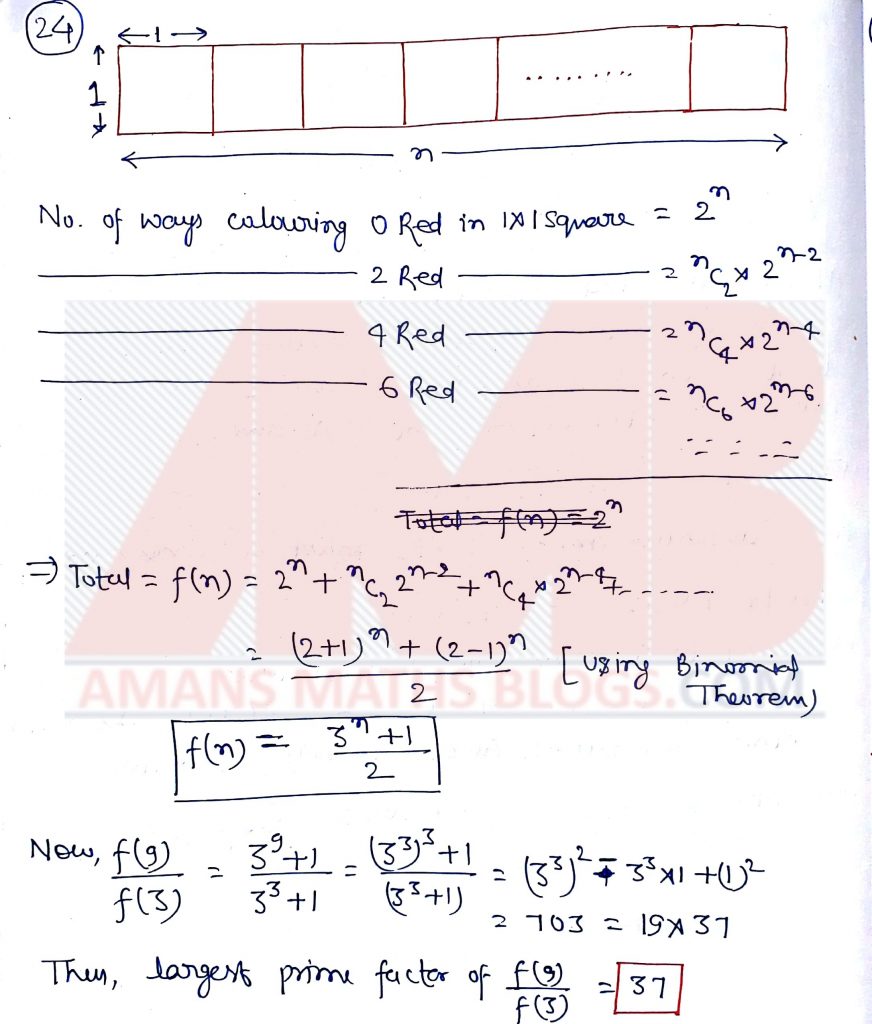
Pre RMO 2019 Question No 24
A 1 x n rectangle ( n ≥ 1) is divide into n unit (1 x 1) squares. Each square of this rectangle is coloured red, blue or green. Let f(n) be the number of colouring of the rectangle in which there are an even number of red squares, What is the largest prime factor of f(9)/f(3)? (The number of red squares can be zero.)
Solution:
Pre RMO 2019 Question No 25
A village has a circular wall around it, and the wall has four gates pointing north, south, east and west. A tree stands outside the village, 16 m east of the south gate. What is the diameter, in meters, of the wall that surrounds the village?
Solution:
Pre RMO 2019 Question No 26
Positive integers x, y, z satisfy xy + z = 160. Compute the smallest possible value of x + yz.
Solution:
Pre RMO 2019 Question No 27
We will say that a rearrangement of the letters of a word has no fixed letters if, when the rearrangement is placed directly the word, no column has the same letter repeated. For instance, H B R A T A is a rearrangement with no fixed letters of B H A R A T have? ( The two As are considered identical.)
Solution:
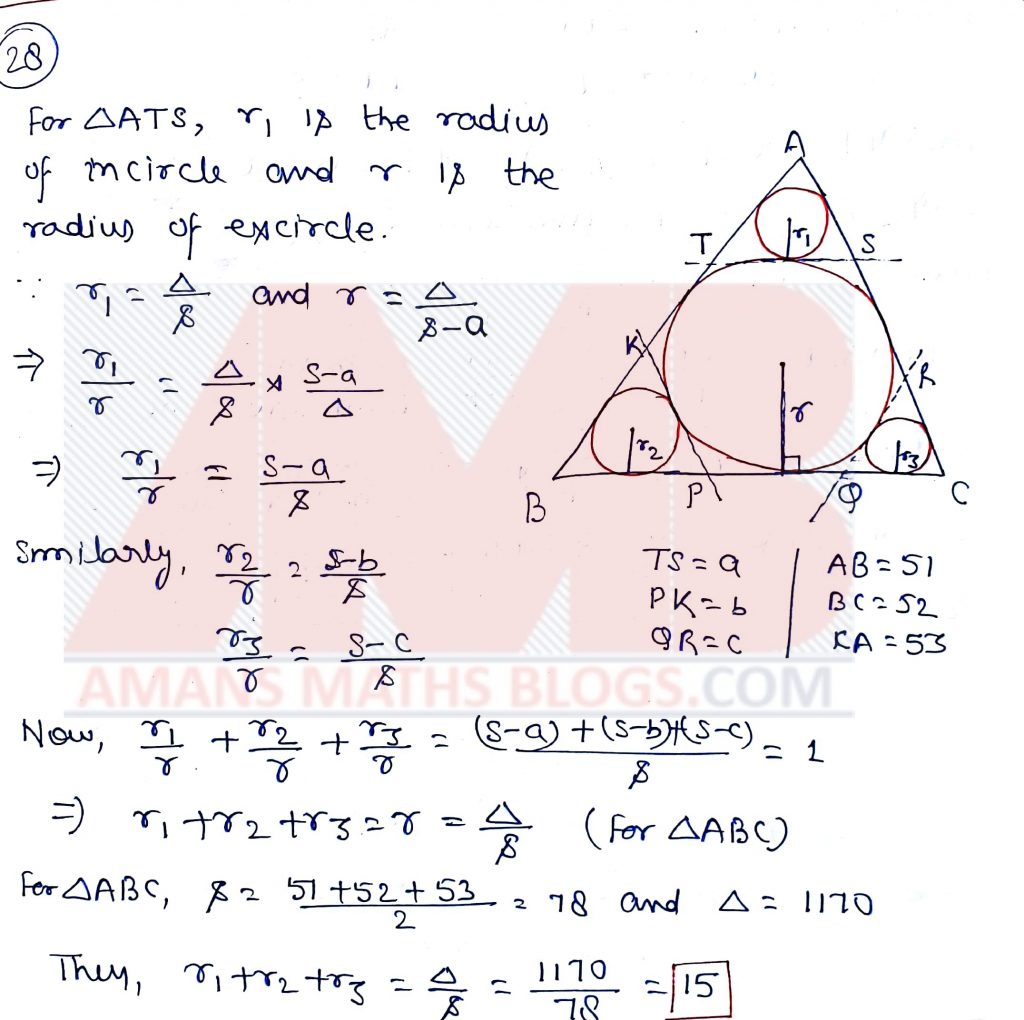
Pre RMO 2019 Question No 28
Let ABC be a triangle with side 51, 52, 53. Let Ω denote the incircle of ∆ABC. Draw tangents to Ω which are parallel to the sides of ABC. Let r1, r2, r3 be the inradii of the three corner triangles so formed. Find the largest integer that does not exceed r1 + r2 + r3.
Solution:
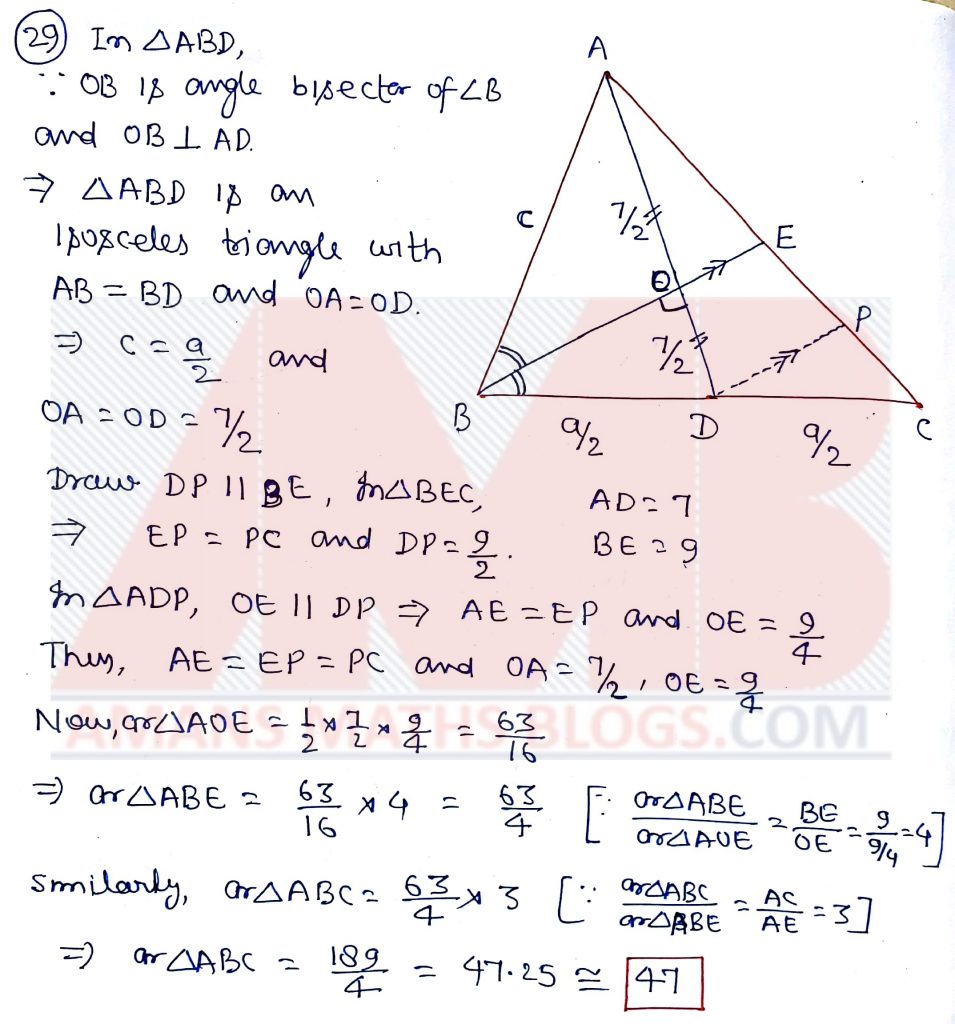
Pre RMO 2019 Question No 29
In a triangle ABC, the median AD ( with D on BC) and the angle bisector BE (with E on AC) are perpendicular to each other. If AD = 7 and BE = 9, find the integer nearest to the area of triangle ABC.
Solution:
Pre RMO 2019 Question No 30
Let E denote the set of all natural numbers n such that 3 < n < 100 and the set {1,2,3,…,n} can be partitioned in to 3 subsets with equal sums. Find the number of elements of E .
Solution: